本系列文章力求以简洁易懂的文字介绍计算几何中的基本概念,使读者快速入门,故不追求难度和深度,仅起到抛砖引玉的作用。


这篇文章我们来好好聊一聊二维计算几何的圆类,三角形类和多边形类。
首先是我们的三角形类,由于我们不经常触及三角形的集合,所以我们一般直接用三角形 的三个顶点来表示一个三角形,也就是三个Point结构体构成的新结构体Triangle:

那么对于三角形这一几何变量的相关运算,一般包含三角形的面积计算,三角形的四心求取,还有一个是三角形的费马点的计算。

这个时候我们的叉积就派上大用场辣~,我觉得海伦公式其实Duck 不必~(蒟蒻见解,勿喷)

对于三角形四心的求解,在上一篇的计算几何——一切的开始中曾说,计算几何是解析几何的一种,那么我们首先来看一下四心的定义和性质:

参考解析几何对四心的求法并且我们借助巧妙的叉积运算:
假设三点坐标为(X1,Y1), (X2,Y2), (X3,Y3)
1.重心

通过几何证明可知,三角形重心坐标为:


2.外心
外心是指三角形三个顶点到外接圆圆心的距离相等,外接圆的半径等于外心到任意一个顶点的距离。外心的坐标公式为:外心的横坐标等于顶点A、B、C坐标的行列式除以2倍三角形的面积的绝对值,纵坐标同理。即外心的坐标为:

( (x1*y2 + x2*y3 + x3*y1 - x1*y3 - x2*y1 - x3*y2) / (2*面积绝对值) , (x1^2 + y1^2)*(y2-y3) + (x2^2 + y2^2)*(y3-y1) + (x3^2 + y3^2)*(y1-y2) / (2*面积绝对值) )

3.垂心

同样利用欧式几何学证明可以推出垂心的坐标,这里我们不做要求,直接上代码:

4.内心

通过面积法和几何性质可得内心为三边的加权平均表示:

关于三角形比较常用的还有一个就是著名的费马点:

那么我们怎么求这个费马点呢?
根据定义,对于最大角大于120°的三角形,我们采用余弦定理直接求得顶点即可;而对于余下的三角形集合,费马点都在三角形的内部,我们又应该如何求得呢?
尺规作图中,我们一般采用画等边三角形的方法:分别以三角形ABC的一边为边长向外作等边三角形,画其外接圆,三个外接圆的交点即为费马点。因此按照这个定义,我们先求出三边引出的三个等边三角形,然后求出三个三角形的外接圆,求出三圆交点。

但是其实单单采用外接圆求交,我们又要用到非常复杂的余弦定理和几何证明了,经过我的推理这个过程还要涉及向量的旋转,还有著名的勾股定理,想想都很麻烦叭~,最重要的是我们还没学过圆类呢~😭QAQ,为了不涉及圆的知识,我们需要对该求解思路做进一步的简化。
对费马点这个几何图形进行短暂的思考可以发现:之所以三圆能共点,并且其它的交点为三角形的三个顶点,我们不难得出AE,CF,BD这三线共费马点,那么这边的几何证明我们不做要求,我就不写出来辣。(对欧式几何感兴的小伙伴可以动手去证明一下,挺简单的~[doge])

OK,我们来总结一下,对于120以上的三角形,我们采用余弦定理直接求点,反之,我们求出两边产生的等边三角形,求出两条三角形顶点与等边三角形的顶点连成的直线的交点,就是我们所求的费马点!

👆 一些必要的三角形预处理~

👆然后这是直线类的定义以及两条直线求交函数~

👆,然后我们就编写费马点的主函数,对于第二种情况,请读者小伙伴自行思考进行编写,就是边求中点 + 法向量,求出等边三角形的顶点!这样子做两次,直接通过交点函数返回的点就是费马点~
好我们接下来开始学习一下多边形:对于ACM的小朋友呃,我们在初高中的时候学的多边形其实都是凸多边形,在计算几何中我们又称其为二维凸包,但是多边形还有一种是凹多边形,这个长得就非常的抽象辣~
所以根据定义,我们直接写多边形结构体Polygon,或者采用点集写法(用点类数组存储)QAQ。那么对于多边形的一些基本运算呢,我们一般都是求解面积,周长等等这些基本要素,其中周长非常简单,就是对多边形点集的线扫(切记要加上首尾相加的边~),那么面积呢?凸多边形的面积非常的简单,就是一个个三角形的面积和,如下图:

那么当凸多边形变成凹多边形这种算法还成立吗o.O?

没错,大家看到的这个离离谱谱抽抽象象的东西就是凹多边形,可以一眼看出这种算法的使用会把相交的三角形的面积也求了,那么答案不就是错了吗?🤔,因此我们需要使用非常智慧的容斥原理重新改良一下这个算法:
类似凸多边形,现将编号以此排序然后,一条一条边枚举,如果逆时针转就面积加,逆时针就减去该面积,容斥之后为凹边形面积,不过无需另外计算旋转方向,因为叉乘时已经计算方向,直接累加即可。
👆当然这个算法也适用于凸多边形,也就是多边形面积的通解~
👇一个非常合理的解释,我们伟大的叉积运算求有向面积:

所以根据叉积运算,我们最终总结出来了多边形面积的求解通式👇:

来看看多边形面积求解的板子题:物理-磁通量,下面给出这个的主程序,赤裸裸的叉积~

然后是几个比较经典的定理:婆罗摩几多公式,欧拉公式,皮克定理(不过感觉没啥用~)

2. 一个小例子——二维凸包
凸包问题是计算几何的核心问题与经典问题,因此我们从二维凸包开始。学完这个例子,会对这门学科的特点有更深的体会。
2.1 凸集和凸包
凸集:平面的一个子集,并且形状是“凸”的。“凸”准确地说就是在集合内部取任意两点p、q,它们连成的线段仍完全处于内部,如下图。

上述就是对于凸包这一概念的描述,在ACM中我们常常需要求出点集的凸包,即从大量的点 中选取若干个点构成凸多边形,使这个凸多边形覆盖剩余所有点~,👇下图就是一个经典的二维 凸包:
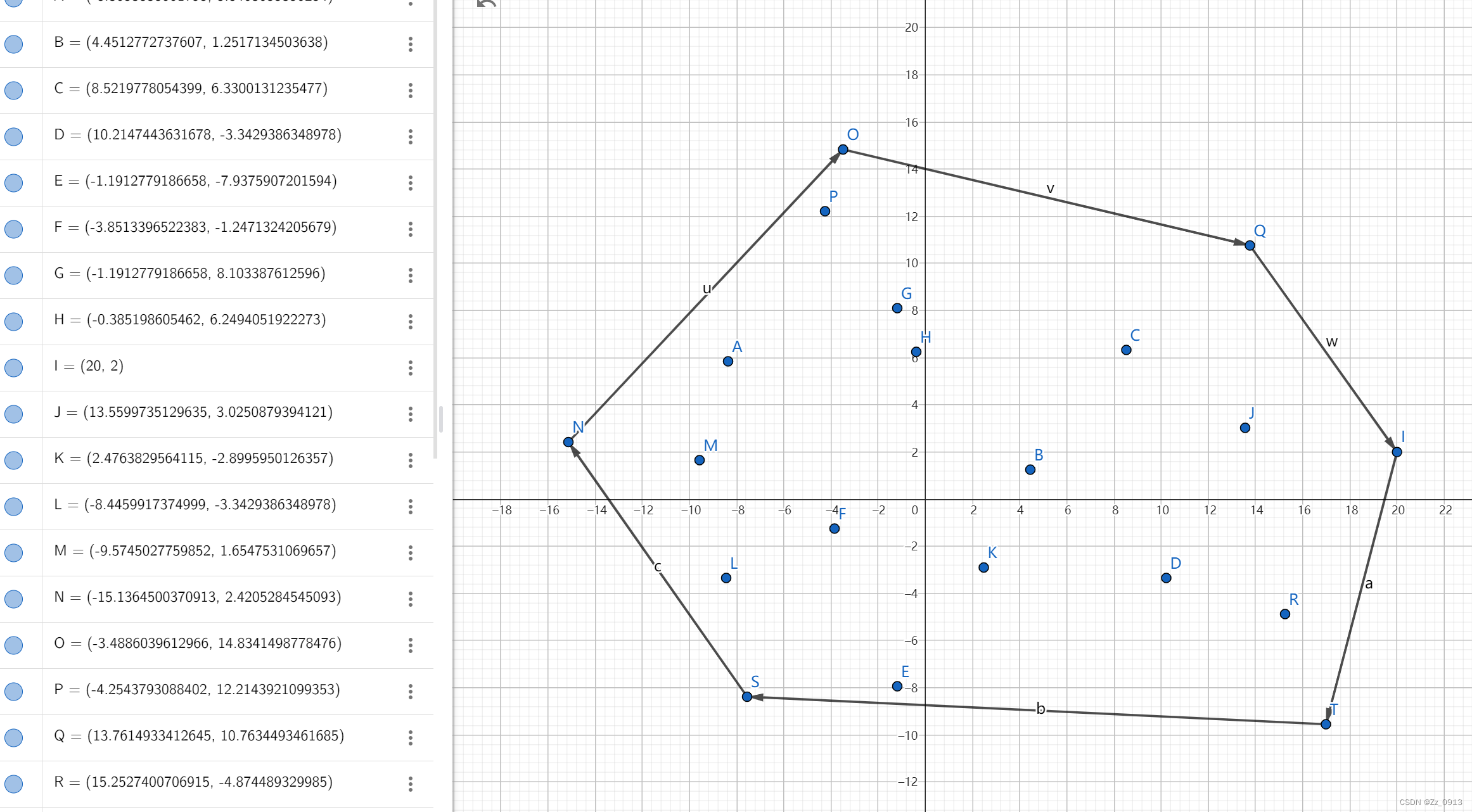
在算法设计中我们需要寻求一种算法,求出这个凸包~🤔
这边我们先介绍一下Graham扫描算法,大概思路就是利用叉积判断两个向量的方向走向是否是顺时针 or 逆时针*,分别求出上凸包和下凸包然后整合成我们需要的凸包。

👆:向量NP和向量PG关系为右拐,PG和GC,以及GC和CQ分别都为左拐关系,应该很好判断
这里说明一下为什么叉积能够做到这个:
在三维向量中,根据右手定则,若向量为右拐,则叉积方向沿Z轴负向;若为左拐,则为Z轴正向。

那么在二维向量中的Z轴方向一直为零,所以根据右手定则和叉积运算,我们可以得出这个结论:
头尾顺次连接的两个向量若其叉乘小于0,则向量右拐,大于(等于)0,则向量左拐🤔(不是很能理解的可以画一个坐标系用两个向量模拟下[doge])那么我们判断是否右拐就这么写:

接下来我们就开始Graham扫描的流程(顺时针):
1.先将所有点按横坐标为第一关键字从小到大排序
2.从小到大开始一个个放入栈stack中,用来存储最终凸包中的点,中间需要判断栈顶 的三个点构成的两个向量是否右拐,假如出现了左拐,则开始逐一出栈,知道栈顶的两个点和新 的一个点构成的两个向量形成右拐~😄
3.重复步骤2,从左到右找到上凸包,再从右到左找到下凸包,最终找到最大的二维凸 包。
接下来用图演示一手:(绿边为符合条件的向量,即右拐
红边为左拐边,不符合条件
蓝边为出现红边之后开始删边后最后完成纠错的一条边)

👆:利用GrahamScan上凸包的求解过程

👆:利用GrahamScan下凸包的求解过程
OK,那么计算几何中的这一经典算法是不是非常好理解,那么赶紧去写写这道简简单单的模板题叭试个水~
P2742 [USACO5.1] 圈奶牛Fencing the Cows /【模板】二维凸包
直接上代码看一下GrahamScan的经典写法叭~
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN = 1e5 + 20;
const double Eps = 1e-9;
int N,i,top1,stk1[MAXN],top2,stk2[MAXN],top,stk[MAXN];
double x,y;
#define Temp template<typename T>
Temp inline void read(T &x)
{
x = 0;
T w = 1,ch = getchar();
while(! isdigit(ch) && ch != '-')
ch = getchar();
if(ch == '-')
w = -1,ch = getchar();
while(isdigit(ch))
x = (x << 3) + (x << 1) + (ch ^ '0'),ch = getchar();
x = x * w;
}
int Sign(double x) { if(fabs(x) < Eps) return 0;if(x > 0) return 1;if(x < 0) return -1;}
struct Point{
double x,y;
Point(double x = 0,double y = 0) : x(x) , y(y) {}
}point[MAXN];
typedef Point Vector;
Vector operator + (Vector Alpha,Vector Beta) { return Vector(Alpha.x + Beta.x,Alpha.y + Beta.y);}
Vector operator - (Vector Alpha,Vector Beta) { return Vector(Alpha.x - Beta.x,Alpha.y - Beta.y);}
Vector operator * (Vector Alpha,double x) { return Vector(Alpha.x * x,Alpha.y * x);}
Vector operator / (Vector Alpha,double x) { return Vector(Alpha.x / x,Alpha.y / x);}
double sqr(double x) { return x * x;}
double dis(Point Alpha,Point Beta) { return sqrt(sqr(Alpha.x - Beta.x) + sqr(Alpha.y - Beta.y));}
bool cmp(const Point &x,const Point &y) { if(x.x < y.x || x.x == y.x && x.y < y.y) return true;else return false;}
bool check(Point Alpha,Point Beta,Point Gama)
{
Vector u = Beta - Alpha,v = Gama - Beta;
if(u.x * v.y - v.x * u.y < 0) return true;else return false;
}
inline void Scan1(int N)
{
top1 = top1 + 1;
stk1[top1] = top1;
top1 = top1 + 1;
stk1[top1] = top1;
for(int i = 3;i <= N;i++)
{
top1 = top1 + 1;
stk1[top1] = i;
while(check(point[stk1[top1 - 2]],point[stk1[top1 - 1]],point[stk1[top1]]) == false && top1 > 2)
{
stk1[top1 - 1] = stk1[top1];
top1 = top1 - 1;
}
}
}
inline void Scan2(int N)
{
top2 = top2 + 1;
stk2[top2] = N;
top2 = top2 + 1;
stk2[top2] = N - 1;
for(int i = N - 2;i >= 1;i--)
{
top2 = top2 + 1;
stk2[top2] = i;
while(check(point[stk2[top2 - 2]],point[stk2[top2 - 1]],point[stk2[top2]]) == false && top2 > 2)
{
stk2[top2 - 1] = stk2[top2];
top2 = top2 - 1;
}
}
}
int main()
{
read(N);
for(int i = 1;i <= N;i++)
{
scanf("%lf%lf",&x,&y);
point[i].x = x,point[i].y = y;
}
sort(point + 1,point + N + 1,cmp);
memset(stk1,0,sizeof(stk1));
top1 = 0;
Scan1(N);
memset(stk2,0,sizeof(stk2));
top2 = 0;
Scan2(N);
for(int i = 1;i <= top1;i++)
{
top = top + 1;
stk[top] = stk1[i];
}
for(int i = 2;i <= top2;i++)
{
top = top + 1;
stk[top] = stk2[i];
}
double ans = 0;
for(int i = 1;i <= top - 1;i++) ans = ans + dis(point[stk[i]],point[stk[i + 1]]);
printf("%.2f\n",ans);
return 0;
}计算几何经过几十年的发展,求解二维凸包已经有许许多多的算法,作为入门教程就不一一列举了。它们特点各异,有的数值稳定性好、有的时间复杂度低、有的易于扩展到高维。我们这里讲的递增式算法其实叫作Andrew算法,是1979年在Graham scan算法的基础上改进而来,十分简单高效且容易理解,是最常用的算法之一,有上述内容作基础再根据实际需要学习其他算法也就很轻松了。
好了,这系列的计算几何主要讲了三角形的几个重要点,以及多边形的入门,仅仅是一些经典公式和算法的分享,之后同系列的文章会做深入。一个非常严重的问题就是,相信读者发现了,计算几何的板子都是又臭又长,这个东西呢在ACM的赛场上有限的时间内需要取舍,对于这个性价比的考量,就比如今年2023年11月的南京站那道B题——交并比,全场没人写出来,有极高的思维含量和长长的代码。

👆:ICPC亚洲赛区南京站的B题——交并比🤔
总结一句,计算几何题目是一类灵活性强,思维含量高而且代码量很大的题目,需要我们慢慢学把基础打扎实了,这样才能在比赛上信手拈来~





















 235
235











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








