MLAPP 读书笔记 - 04-1 高斯模型(Gaussian models)

MLAPP 读书笔记 - 04 高斯模型(Gaussian models)

A Chinese Notes of MLAPP，MLAPP 中文笔记项目
https://zhuanlan.zhihu.com/python-kivy

转载：cycleuser

侵权立删，本意是为广大学习爱好者提供中文资料，同时在这里补充了图片，方便阅读，如果有任何法律问题，我会立即删除。

4.1 简介

本章要讲的是多元高斯分布(multivariate Gaussian),或者多元正态分布(multivariate normal ,缩写为MVN)模型,这个分布是对于连续变量的联合概率密度函数建模来说最广泛的模型了.未来要学习的其他很多模型也都是以此为基础的.

然而很不幸的是,本章所要求的数学水平也是比很多其他章节都要高的.具体来说是严重依赖线性代数和矩阵积分.要应对高维数据,这是必须付出的代价.初学者可以跳过标记了星号的章.另外本章有很多等式,其中特别重要的用方框框了起来.

4.1.1 记号

这里先说几句关于记号的问题.向量用小写字母粗体表示,比如x.矩阵用大写字母粗体表示,比如X.大写字母加下标表示矩阵中的项,比如$X_{ij}$.
所有向量都假设为列向量(column vector),除非特别说明是行向量.通过堆叠(stack)D个标量(scalar)得到的类向量记作$[x_1,...,x_D]$.与之类似,如果写x=$[x_1,...,x_D]$,那么等号左侧就是一个高列向量(tall column vector),意思就是沿行堆叠$x_i$,一般写作x=$(x_1^T,...,x_D^T{)}^T$,不过这样很丑哈.如果写X=$[x_1,...,x_D]$,等号左边的是矩阵,意思就是沿列堆叠$x_i$,建立一个矩阵.

4.1.2 基础知识

回想一下本书2.5.2中关于D维度下的多元正态分布(MVN)概率密度函数(pdf)的定义,如下所示:
$N(x|\mu ,\Sigma )\stackrel{\ast }{=}\frac{1}{(2\pi {)}^{D/2}|\Sigma {|}^{1/2}}\exp [-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )]$(4.1 重要公式)

此处参考原书图4.1

指数函数内部的是一个数据向量x和均值向量**$\mu$** 之间的马氏距离(马哈拉诺比斯距离,Mahalanobis distance).对$\Sigma$进行特征分解(eigendecomposition)有助于更好理解这个量.$\Sigma =U\Lambda U^T$,其中的U是标准正交矩阵(orthonormal matrix),满足$U^{T}U=I$,而$\Lambda$是特征值组成的对角矩阵.经过特征分解就得到了:

${\Sigma }^{-1}=U^{-T}{\Lambda }^{-1}{U}^{-1}=U{\Lambda }^{-1}{U}^T={\sum }_{i=1}^D\frac{1}{{\lambda }_i}{u}_i{u}_i^T$(4.2)

上式中的$u_i$是U的第i列,包含了第i个特征向量(eigenvector).因此就可以把马氏距离写作:

$$\begin{array}{rlr}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )& =(x-\mu {)}^T(\sum _{i=1}^D\frac{1}{{\lambda }_i}{u}_i{u}_i^T)(x-\mu )& \text{(4.3)}\\ & =\sum _{i=1}^D\frac{1}{{\lambda }_i}(x-\mu {)}^T{u}_i{u}_i^T(x-\mu )=\sum _{i=1}^D\frac{y_i^2}{{\lambda }_i}& \text{(4.4)}\end{array}$$

上式中的$y_i\stackrel{\ast }{=}{u}_i^T(x-\mu )$.二维椭圆方程为:
$\frac{y_1^2}{{\lambda }_1}+\frac{y_2^2}{{\lambda }_2}=1$(4.5)

因此可以发现高斯分布的概率密度的等值线沿着椭圆形,如图4.1所示.特征向量决定了椭圆的方向,特征值决定了椭圆的形态即宽窄比.

一般来说我们将马氏距离(Mahalanobis distance)看作是对应着变换后坐标系中的欧氏距离(Euclidean distance),平移$\mu$,旋转U.

4.1.3 多元正态分布(MVN)的最大似然估计(MLE)

接下来说的是使用最大似然估计(MLE)来估计多元正态分布(MVN)的参数.在后面的章节里面还会说道用贝叶斯推断来估计参数,能够减轻过拟合,并且能对估计值的置信度提供度量.

定理4.1.1(MVN的MLE)

如果有N个独立同分布样本符合正态分布,即$x_i\sim N(\mu ,\Sigma )$,则对参数的最大似然估计为:
${\hat{\mu }}_{mle}=\frac{1}{N}{\sum }_{i=1}^N{x}_i\stackrel{\ast }{=}\bar{x}$(4.6)
${\hat{\Sigma }}_{mle}=\frac{1}{N}{\sum }_{i=1}^N(x_i-\bar{x})(x_i-\bar{x}{)}^T=\frac{1}{N}({\sum }_{i=1}^N{x}_i{x}_i^T)-\bar{x}{\bar{x}}^T$(4.7)

也就是MLE就是经验均值(empirical mean)和经验协方差(empirical covariance).在单变量情况下结果就很熟悉了:
$\hat{\mu }=\frac{1}{N}{\sum }_i{x}_i=\bar{x}$(4.8)
${\hat{\sigma }}^2=\frac{1}{N}{\sum }_i(x_i-x{)}^2=(\frac{1}{N}{\sum }_i{x}_i^2)-{\bar{x}}^2$(4.9)

4.1.3.1 证明

要证明上面的结果,需要一些矩阵代数的计算,这里总结一下.等式里面的a和b都是向量,A和B都是矩阵.记号$tr(A)$表示的是矩阵的迹(trace),是其对角项求和,即$tr(A)={\sum }_i{A}_{ii}$.

$\begin{array}{rl}\frac{\partial (b^{T}a)}{\partial a}& =b\\ \frac{\partial (a^{T}Aa)}{\partial a}& =(A+A^T)a\\ \frac{\partial }{\partial A}tr(BA)& =B^T\\ \frac{\partial }{\partial A}\log |A|& =A^{-T}\stackrel{\ast }{=}(A^{-1}{)}^T\\ tr(ABC)=tr(CAB)& =tr(BCA)\end{array}$

(4.10 重要公式)

上式中最后一个等式也叫做迹运算的循环置换属性(cyclic permutation property).利用这个性质可以推广出很多广泛应用的求迹运算技巧,对标量内积$x^{T}Ax$就可以按照如下方式重新排序:
$x^{T}Ax=tr(x^{T}Ax)=tr(x{x}^{T}A)=tr(Ax{x}^T)$(4.11)

证明过程

接下来要开始证明了,对数似然函数为:

$l(\mu ,\Sigma )=\log p(D|\mu ,\Sigma )=\frac{N}{2}\log |\Lambda |-\frac{1}{2}{\sum }_{i=1}^N(x_i-\mu {)}^T\Lambda (x_i-\mu )$(4.12)

上式中$\Lambda ={\Sigma }^{-1}$,是精度矩阵(precision matrix)

然后进行一个替换(substitution)$y_i=x_i-\mu$,再利用微积分的链式法则:

$\begin{array}{rlr}\frac{\partial }{\partial \mu }(x_i-\mu {)}^T{\Sigma }^{-1}(x_i-\mu )& =\frac{\partial }{\partial y_i}{y}_i^T{\Sigma }^{-1}{y}_i\frac{\partial y_i}{\partial \mu }& \text{(4.13)}\\ & =-1({\Sigma }_{-1}+{\Sigma }^{-T})y_i& \text{(4.14)}\end{array}$

因此：

$\begin{array}{rlr}\frac{\partial }{\partial \mu }l(\mu .\Sigma )& =-\frac{1}{2}\sum _{i=1}^N-2{\Sigma }^{-1}(x_i-\mu )={\Sigma }^{-1}\sum _{i=1}^N(x_i-\mu )=0& \text{(4.15)}\\ & =-1({\Sigma }_{-1}+{\Sigma }^{-T})y_i& \text{(4.16)}\end{array}$

所以$\mu$的最大似然估计(MLE)就是经验均值(empirical mean).

然后利用求迹运算技巧(trace-trick)来重写对$\Lambda$的对数似然函数:

$\begin{array}{rlr}l(\Lambda )& =\frac{N}{2}\log |\Lambda |-\frac{1}{2}\sum _{i}tr[(x_i-\mu )(x_i-\mu {)}^T\Lambda ]& \text{(4.17)}\\ & =\frac{N}{2}\log |\Lambda |-\frac{1}{2}tr[S_{\mu }\Lambda ]& \text{(4.18)}\\ & & \text{(4.19)}\end{array}$

上式中
$S_{\mu }\stackrel{\ast }{=}{\sum }_{i=1}^N(x_i-\mu )(x_i-\mu {)}^T$(4.20)

是以$\mu$为中心的一个散布矩阵(scatter matrix).对上面的表达式关于$\Lambda$进行求导就得到了:

$\begin{array}{rlr}\frac{\partial l(\Lambda )}{\partial \Lambda }& =\frac{N}{2}{\Lambda }^{-T}-\frac{1}{2}{S}_{\mu }^T=0& \text{(4.21)}\\ {\Lambda }^{-T}& ={\Lambda }^{-1}=\Sigma =\frac{1}{N}{S}_{\mu }& \text{(4.22)}\end{array}$

因此有:
$\hat{\Sigma }=\frac{1}{N}{\sum }_{i=1}^N(x_i-\mu )(x_i-\mu {)}^T$(4.23)

正好也就是以$\mu$为中心的经验协方差矩阵(empirical covariance matrix).如果插入最大似然估计$\mu =\bar{x}$(因为所有参数都同时进行优化),就得到了协方差矩阵的最大似然估计的标准方程.

4.1.4 高斯分布最大熵推导(Maximum entropy derivation of the Gaussian)

在本节,要证明的是多元高斯分布(multivariate Gaussian)是适合于有特定均值和协方差的具有最大熵的分布(参考本书9.2.6).这也是高斯分布广泛应用到一个原因,均值和协方差这两个矩(moments)一般我们都能通过数据来进行估计得到(注:一阶矩（期望）归零，二阶矩（方差）),所以我们就可以使用能捕获这这些特征的分布来建模,另外还要尽可能少做附加假设.

为了简单起见,假设均值为0.那么概率密度函数(pdf)就是:
$p(x)=\frac{1}{Z}\exp (-\frac{1}{2}{x}^T{\Sigma }^{-1}x)$(4.24)

如果定义 f i j ( x ) = x i x j , λ i j = 1 2 ( Σ − 1 ) i j , i , j ∈ { 1 , . . . , D } f_{ij} (x) = x_i x_j , \lambda_{ij} = \frac{1}{2} (\Sigma^{-1})_{ij}, i, j \in \{1, ... , D\} fij​(x)=xi​xj​,λij​=21​(Σ−1)ij​,i,j∈{1,...,D},就会发现这个和等式9.74形式完全一样.这个分布（使用自然底数求对数）的（微分）熵为:
$h(N(\mu ,\Sigma ))=\frac{1}{2}\ln [(2\pi e{)}^D|\Sigma |]$(4.25)

接下来要证明有确定的协方差$\Sigma$的情况下多元正态分布(MVN)在所有分布中有最大熵.

定理 4.1.2

设$q(x)$是任意的一个密度函数,满足$\int q(x)x_i{x}_j={\Sigma }_{ij}$.设$p=N(0,\Sigma )$.那么$h(q)\le h(p)$.

证明.(参考(Cover and Thomas 1991, p234)).
(注:KL是KL 散度(Kullback-Leibler divergence),也称相对熵(relative entropy),可以用来衡量p和q两个概率分布的差异性(dissimilarity).更多细节参考2.8.2.)

$\begin{array}{rlr}0& \le KL(q||p)=\int q(x)\log \frac{q(x)}{p(x)}dx& \text{(4.26)}\\ & =-h(q)-\int q(x)\log p(x)dx& \text{(4.27)}\\ & \stackrel{\ast }{=}-h(q)-\int ps(x)\log p(x)dx& \text{(4.28)}\\ & =-h(q)+h(p)& \text{(4.29)}\end{array}$

等式4.28那里的星号表示这一步是关键的,因为q和p对于由$\log p(x)$编码的二次形式产生相同的矩(moments).

4.2 高斯判别分析(Gaussian discriminant analysis)*

多元正态分布的一个重要用途就是在生成分类器中定义类条件密度,也就是:
$p(x|y=c,\theta )=N(x|{\mu }_c,{\Sigma }_c)$(4.30)

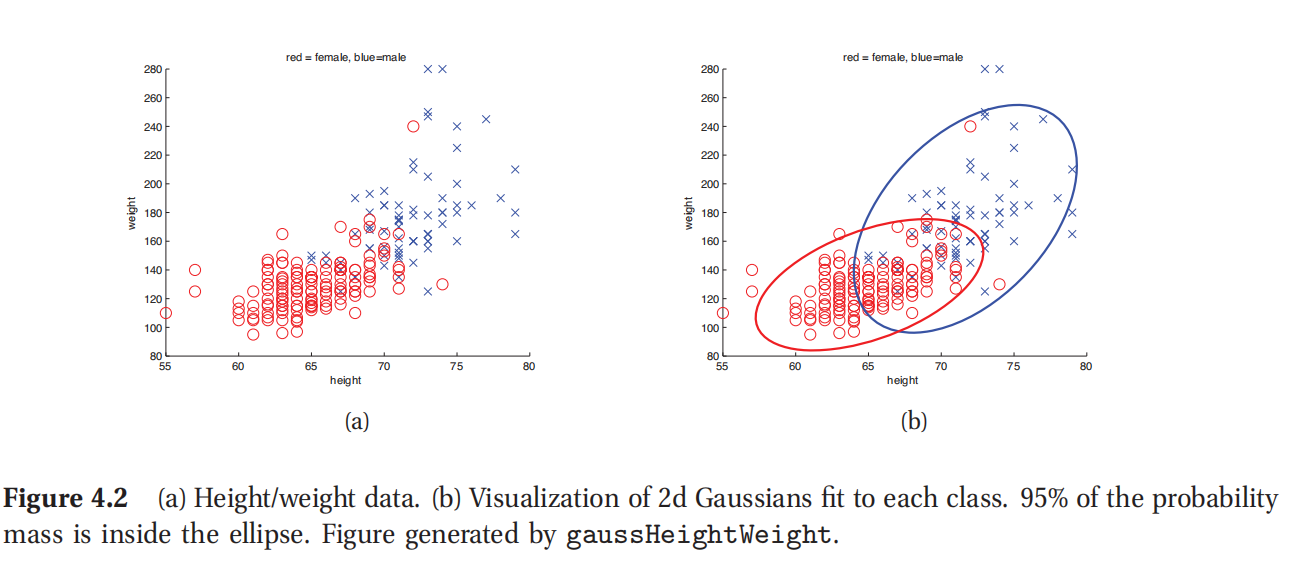
这样就得到了高斯判别分析,也缩写为GDA,不过这其实还是生成分类器(generative classifier）,而并不是辨别式分类器（discriminative classifier）,这两者的区别参考本书8.6.如果${\Sigma }_c$是对角矩阵,那这就等价于朴素贝叶斯分类器了.

此处参考原书图4.2

从等式2.13可以推导出来下面的决策规则,对一个特征向量进行分类:
$\hat{y}(x)=\arg {\max }_c[\log p(y=c|\pi )+\log p(x|{\theta }_c)]$(4.31)

计算x 属于每一个类条件密度的概率的时候,测量的距离是x到每个类别中心的马氏距离(Mahalanobis distance).这也是一种最近邻质心分类器(nearest centroids classifier).

例如图4.2展示的就是二维下的两个高斯类条件密度,横纵坐标分别是身高和体重,包含了男女两类人.很明显身高体重这两个特征有相关性,就如同人们所想的,个子高的人更可能重.每个分类的椭圆都包含了95%的概率质量.如果对两类有一个均匀分布的先验,就可以用如下方式来对新的测试向量进行分类:

$\hat{y}(x)=\arg {\min }_c(x-{\mu }_c{)}^T{\Sigma }_c^{-1}(x-{\mu }_c)$(4.32)

4.2.1 二次判别分析(Quadratic discriminant analysis,QDA)

对类标签的后验如等式2.13所示.加入高斯密度定义后,可以对这个模型获得更进一步的理解:
$p(y=c|x,\theta )=\frac{{\pi }_c|2\pi {\Sigma }_c{|}^{-1/2}\exp [-1/2(x-{\mu }_c{)}^T{\Sigma }_c^{-1}(x-{\mu }_c)]}{{\Sigma }_{c^{\prime }}{\pi }_{c^{\prime }}|2\pi {\Sigma }_{c^{\prime }}{|}^{-1/2}\exp [-1/2(x-{\mu }_{c^{\prime }}{)}^T{\Sigma }_{c^{\prime }}^{-1}(x-{\mu }_{c^{\prime }})]}$(4.33)

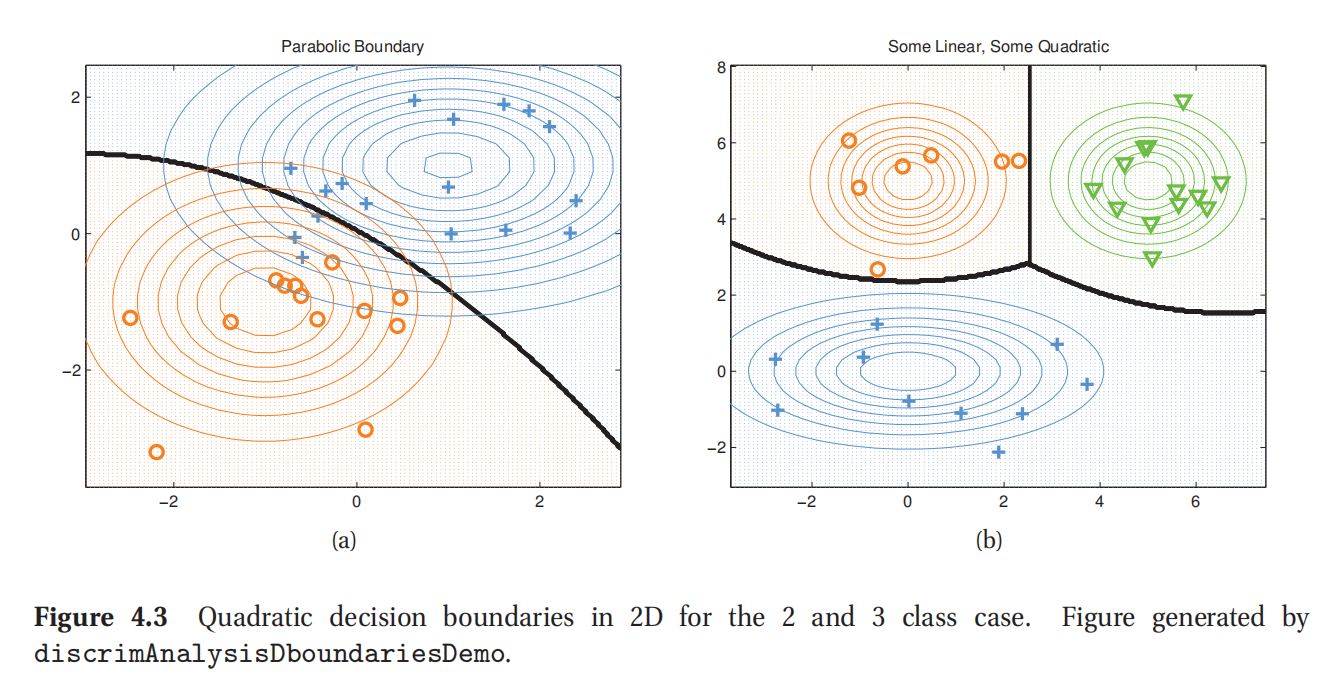
对此进行阈值处理(thresholding)就得到了一个x的二次函数(quadratic function).这个结果也叫做二次判别分析(quadratic discriminant analysis,缩写为QDA).图4.3所示的是二维平面中决策界线的范例.

此处参考原书图4.3

此处参考原书图4.4

4.2.2 线性判别分析(Linear discriminant analysis,LDA)

接下来考虑一种特殊情况,此时协方差矩阵为各类所共享(tied or shared),即${\Sigma }_c=\Sigma$.这时候就可以把等式4.33简化成下面这样:

$\begin{array}{rlr}p(y=c|x,\theta )& \propto {\pi }_c\exp [{\mu }_c^T{\Sigma }^{-1}x-\frac{1}{2}{x}^T{\Sigma }^{-1}x-\frac{1}{2}{\mu }_c^T{\Sigma }^{-1}{\mu }_c]& \text{(4.34)}\\ & =\exp [{\mu }_c^T{\Sigma }^{-1}x-\frac{1}{2}{\mu }_c^T{\Sigma }^{-1}{\mu }_c+\log {\pi }_c]\exp [-\frac{1}{2}{x}^T{\Sigma }^{-1}x]& \text{(4.35)}\end{array}$

由于二次项$x^T{\Sigma }^{-1}$独立于类别c,所以可以抵消掉分子分母.如果定义了:

$\begin{array}{rlr}{\gamma }_c& =-\frac{1}{2}{\mu }_c^T{\Sigma }^{-1}{\mu }_c+\log {\pi }_c& \text{(4.36)}\\ & \text{(4.37)}& \\ {\beta }_c& ={\Sigma }^{-1}{\mu }_c& \end{array}$

则有:
$p(y=c|x,\theta )=\frac{e^{{\beta }_c^T+{\gamma }_c}}{{\Sigma }_{c^{\prime }}{e}^{{\beta }_{c^{\prime }}^T+{\gamma }_{c^{\prime }}}}=S(\eta {)}_c$(4.38)

当$\eta =[{\beta }_1^{T}x+{\gamma }_1,...,{\beta }_C^{T}x+{\gamma }_C]$的时候,$S$就是Softmax函数(softmax function,注:柔性最大函数,或称归一化指数函数),其定义如下:
$S(\eta /T)=\frac{e^{{\eta }_c}}{{\sum }_{c^{\prime }=1}^C{e}^{{\eta }_{c^{\prime }}}}$(4.39)

Softmax函数如同其名中的Max所示,有点像最大函数.把每个${\eta }_c$除以一个常数T,这个常数T叫做温度(temperature).然后让T趋于零,即$T\to 0$,则有:

$$S(\eta /T{)}_c=\{\begin{array}{ll}1.0& \text{if }c=\arg {\max }_{c^{\prime }}{\eta }_{c^{\prime }}\\ 0.0& \text{otherwise}\end{array}$$(4.40)

也就是说,在低温情况下,分布总体基本都出现在最高概率的状态下,而在高温下,分布会均匀分布于所有状态.参见图4.4以及其注解.这个概念来自统计物理性,通常称为玻尔兹曼分布(Boltzmann distribution),和Softmax函数的形式一样.

等式4.38的一个有趣性质是,如果取对数,就能得到一个关于x的线性函数,这是因为$x^T{\Sigma }^{-1}x$从分子分母中约掉了.这样两个类 c 和 c’之间的决策边界就是一条直线了.所以这种方法也叫做线性判别分析(linear discriminant analysis,缩写为LDA).可以按照如下方式来推导出这条直线的形式:

$\begin{array}{rlr}p(y=c|x,\theta )& =p(y=c^{\prime }|x,\theta )& \text{(4.41)}\\ {\beta }_c^{T}x+{\gamma }_c& ={\beta }_{c^{\prime }}^{T}x+{\gamma }_{c^{\prime }}& \text{(4.42)}\\ x^T({\beta }_{c^{\prime }}-\beta )& ={\gamma }_{c^{\prime }}-{\gamma }_c& \text{(4.43)}\end{array}$

样例参考图4.5.

除了拟合一个线性判别分析(LDA)模型然后推导类后验之外,还有一种办法就是对某$C\times D$权重矩阵(weight matrix)W,直接拟合$p(y|x,W)=Cat(y|Wx)$.这叫做多类逻辑回归(multi-class logistic regression)或者多项逻辑回归(multinomial logistic regression).此类模型的更多细节将在本书8.2中讲解,两种方法的区别在本书8.6中有解释.

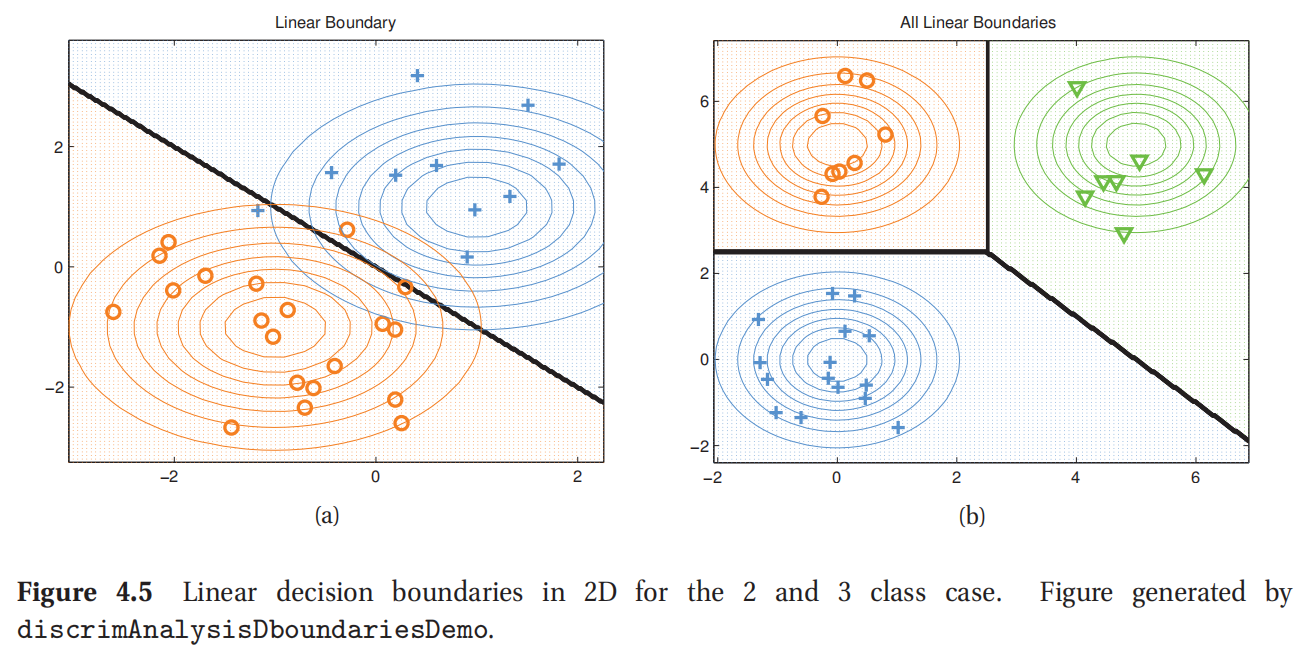
此处查看原书图4.5

此处查看原书图4.6

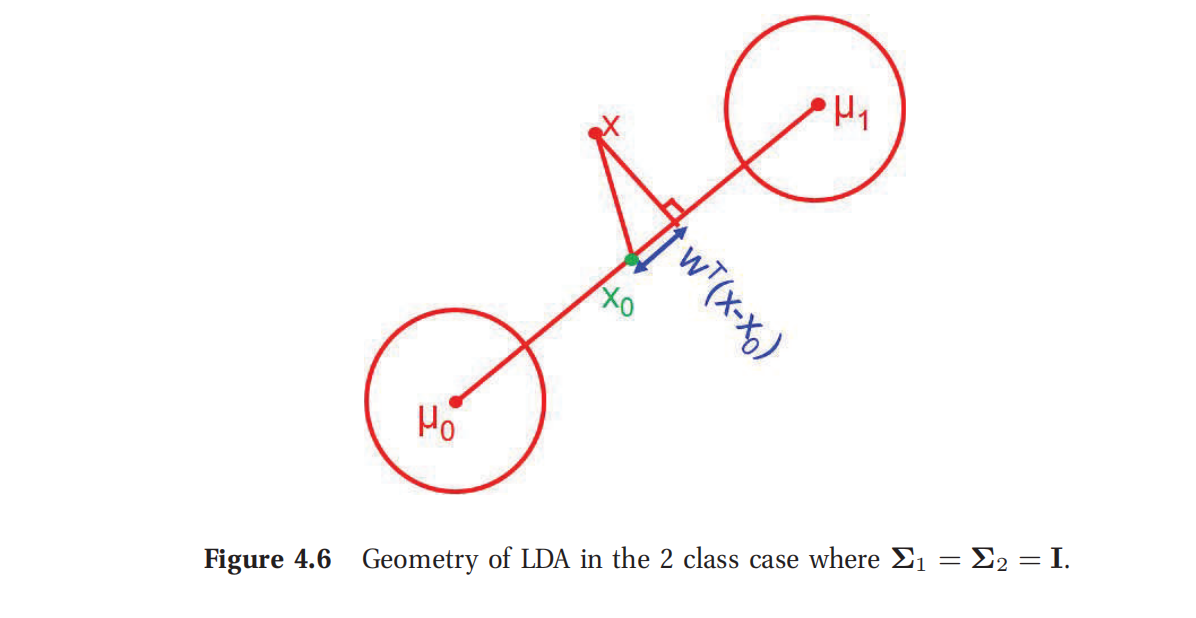
4.2.3 双类线性判别分析(Two-class LDA)

为了更好理解上面那些等式,咱们先考虑二值化分类的情况.这时候后验为:

$\begin{array}{rlr}p(y=1|x,\theta )& =\frac{e^{{\beta }_1^{T}x+{\gamma }_1}}{e^{{\beta }_1^{T}x+{\gamma }_1}+e^{{\beta }_0^{T}x+{\gamma }_0}}& \text{(4.44)}\\ & =\frac{1}{1+e^{({\beta }_0-{\beta }_1){)}^{T}x+({\gamma }_0-{\gamma }_1)}}=sigm(({\beta }_1-{\beta }_0{)}^{T}x+({\gamma }_1-{\gamma }_0))& \text{(4.45)}\end{array}$

上式中的$sigm(\eta )$就是之前在等式1.10中提到的S型函数(sigmoid function).现在则有:

$\begin{array}{rlr}{\gamma }_1-{\gamma }_0& =-\frac{1}{2}{\mu }_1^T{\Sigma }^{-1}{\mu }_1+\frac{1}{2}{\mu }_0^T{\Sigma }^{-1}{\mu }_0+\log ({\pi }_1/{\pi }_0)& \text{(4.46)}\\ & =-\frac{1}{2}({\mu }_1-{\mu }_0{)}^T{\Sigma }^{-1}({\mu }_1+{\mu }_0)+\log ({\pi }_1/{\pi }_0)& \text{(4.47)}\end{array}$

所以如果定义:

$\begin{array}{rlr}w& ={\beta }_1-{\beta }_0={\Sigma }^{-1}({\mu }_1-{\mu }_0)& \text{(4.48)}\\ x_0& =-\frac{1}{2}({\mu }_1+{\mu }_0)-({\mu }_1-{\mu }_0)\frac{\log ({\pi }_1/{\pi }_0)}{({\mu }_1-{\mu }_0{)}^T{\Sigma }^{-1}({\mu }_1-{\mu }_0)}& \text{(4.49)}\end{array}$

然后就有$w^T{x}_0=-({\gamma }_1-{\gamma }_0)$,因此:
$p(y=1|x,\theta )=sigm(w^T(x-x_0))$ (4.50)

这个形式和逻辑回归(logistic regression)关系密切,对此将在本书8.2中讨论.所以最终的决策规则为:将x移动$x_0$,然后投影到线w上,看结果的正负号.
如果$\Sigma ={\sigma }^{2}I$,那么w就是${\mu }_1-{\mu }_0$的方向.我们对点进行分类就要根据其投影距离${\mu }_1$和${\mu }_0$哪个更近.如图4.6所示.另外,如果${\pi }_1={\pi }_0$,那么$x_0=\frac{1}{2}({\mu }_1+{\mu }_0)$,正好在两个均值的中间位置.如果让${\pi }_1>{\pi }_0$,则$x_0$更接近${\mu }_0$,所以图中所示线上更多位置属于类别1.反过来如果${\pi }_1<{\pi }_0$则边界右移.因此,可以看到类的先验${\pi }_c$只是改变了决策阈值,而并没有改变总体的结合形态.类似情况也适用于多类情景.

w的大小决定了对数函数的陡峭程度,取决于均值相对于方差的平均分离程度.在心理学和信号检测理论中,通常定义一个叫做敏感度指数(sensitivity index,也称作 d-prime)的量,表示信号和背景噪声的可区别程度:

$d^{\prime }\stackrel{\ast }{=}\frac{{\mu }_1-{\mu }_0}{\sigma }$(4.51)

上式中的${\mu }_1$是信号均值,${\mu }_0$是噪音均值,而$\sigma$是噪音的标准差.如果敏感度指数很大,那么就意味着信号更容易从噪音中提取出来.

4.2.4 对于判别分析(discriminant analysis)的最大似然估计(MLE)

现在来说说如何去拟合一个判别分析模型(discriminant analysis model).最简单的方法莫过于最大似然估计(maximum likelihood).对应的对数似然函数(log-likelihood)如下所示:

$\log p(D|\theta )=[{\sum }_{i=1}^N{\sum }_{c=1}^{C}I(y_i=c)\log {\pi }_c]+{\sum }_{c=1}^C[{\sum }_{i:y_i=c}\log N(x|{\mu }_c,{\Sigma }_c)]$(4.52)

显然这个式子可以因式分解成一个含有$\pi$的项,以及对应每个${\mu }_c,{\Sigma }_c$的C个项.因此可以分开对这些参数进行估计.对于类先验(class prior),有${\hat{\pi }}_c=\frac{N_c}{N}$,和朴素贝叶斯分类器里一样.对于类条件密度(class-conditional densities),可以根据数据的类别标签来分开,对于每个高斯分布进行最大似然估计:

${\hat{\mu }}_c=\frac{1}{N_c}{\sum }_{i:y_i=c}{x}_i,{\hat{\Sigma }}_c=\frac{1}{N_c}{\sum }_{i:y_i=c}(x_i-{\hat{\mu }}_c)(x_i-{\hat{\mu }}_c{)}^T$(4.53)

具体实现可以参考本书配套的PMTK3当中的discrimAnalysisFit是MATLAB代码.一旦一个模型拟合出来了,就可以使用discrimAnalysisPredict来进行预测了,具体用到的是插值近似(plug-in approximation).

4.2.5 防止过拟合的策略

最大似然估计(MLE)的最大优势之一就是速度和简洁.然而,在高维度数据的情况下,最大似然估计可能会很悲惨地发生过拟合.尤其是当$N_c<D$,全协方差矩阵(full covariance matrix)是奇异矩阵的时候(singular),MLE方法很容易过拟合.甚至即便$N_c>D$,MLE也可能是病态的(ill-conditioned),意思就是很接近奇异.有以下几种方法来预防或解决这类问题:

• 假设类的特征是有条件独立的(conditionally independent),对这些类使用对角协方差矩阵(diagonal covariance matrix);这就等价于使用朴素贝叶斯分类器了,参考本书3.5.
• 使用一个全协方差矩阵,但强制使其对于所有的类都相同,即${\Sigma }_c=\Sigma$.这称为参数绑定(parameter tying)或者参数共享(parameter sharing),等价于线性判别分析(LDA),参见本书4.2.2.
• 使用一个对角协方差矩阵,强迫共享.这叫做对角协方差线性判别分析,参考本书4.2.7.
• 使用全协方差矩阵,但倒入一个先验,然后整合.如果使用共轭先验(conjugate prior)就能以闭合形式(closed form)完成这个过程,利用了本书4.6.3当中的结果;这类似于本书3.5.1.2当中提到的使用贝叶斯方法的朴素贝叶斯分类器(Bayesian naive Bayes),更多细节参考 (Minka 2000f).
• 拟合一个完整的或者对角协方差矩阵,使用最大后验估计(MAP estimate),接下来会讨论两种不同类型的实现.
• 将数据投影到更低维度的子空间,然后在子空间中拟合其高斯分布.更多细节在本书8.6.3.3,其中讲了寻找最佳线性投影(即最有区分作用)的方法.

接下来说一些可选类型.

4.2.6 正交线性判别分析(Regularized LDA)*

假如我们在线性判别分析中绑定了协方差矩阵,即${\Sigma }_c=\Sigma$,接下来就要对$\Sigma$进行最大后验估计了,使用一个逆向Wishart先验,形式为$IW(diag({\hat{\Sigma }}_{mle}),v_0)$,更多内容参考本书4.5.1.然后就有了:

$\hat{\Sigma }=\lambda diag({\hat{\Sigma }}_{mle})+(1-\lambda ){\hat{\Sigma }}_{mle}$(4.54)

上式中的$\lambda$控制的是正则化规模(amount of regularization),这和先验强度(strength of the prior),$v_0$有关,更多信息参考本书4.6.2.1.这个技巧就叫做正则化线性判别分析(regularized discriminant analysis,缩写为 RDA,出自Hastie et al. 2009, p656).

当对类条件密度进行评估的时候,需要计算${\hat{\Sigma }}^{-1}$,也就要计算${\hat{\Sigma }}_{mle}^{-1}$,如果$D>N$那就没办法计算了.不过可以利用对矩阵X的奇异值分解（Singular Value Decomposition,缩写为SVD,参考本书12.2.3)来解决这个问题,如下面所述.(注意这个方法不能用于二次判别分析QDA,因为QDA不是关于x 的线性函数,是非线性函数了.)

设$X=UD{V}^T$是对设计矩阵(design matrix)的SVD分解,其中的V/U分别是$D\times N$和$N\times N$的正交矩阵(orthogonal matrix),而D是规模为N的对角矩阵(diagonal matrix).定义一个$N\times N$的矩阵$Z=UD$;这就像是一个在更低维度空间上的设计矩阵,因为我们假设了$N<D$.另外定义${\mu }_z=V^T\mu$作为降维空间中的数据均值;可以通过$mu=V{\mu }_z$来恢复到原始均值,因为$V^{T}V=V{V}^T=I$.有了这些定义之后,就可以把最大似然估计(MLE)改写成下面的形式了:

$\begin{array}{rlr}& & \\ {\hat{\Sigma }}_{mle}& =\frac{1}{N}{X}^{T}X-\mu {\mu }^T& \text{(4.55)}\\ & =\frac{1}{N}(Z{V}^T{)}^T(Z{V}^T)-(V\mu -z)(V{\mu }_z{)}^T& \text{(4.56)}\\ & =\frac{1}{N}V{Z}^{T}Z{V}^T-V{\mu }_z{\mu }_z^T{V}^T& \text{(4.57)}\\ & =V(\frac{1}{N}{Z}^{T}Z-{\mu }_z{\mu }_z^T)V^T& \text{(4.58)}\\ & =V{\hat{\Sigma }}_z{V}^T& \text{(4.59)}\end{array}$

上式中的${\hat{\Sigma }}_z$是Z的经验协方差(empirical covariance).因此要重新写成最大后验估计(MAP)为:

$\begin{array}{rlr}{\hat{\Sigma }}_{map}& =V{\tilde{\Sigma }}_z{V}^T& \text{(4.60)}\\ {\tilde{\Sigma }}_z& =\lambda diag({\hat{\Sigma }}_z)+(1-\lambda ){\hat{\Sigma }}_z& \text{(4.61)}\end{array}$

注意,我们并不需要真正去计算出来这个$D\times D$矩阵${\hat{\Sigma }}_{map}$.这是因为等式4.38告诉我们,要使用线性判别分析(LDA)进行分类,唯一需要计算的也就是$p(y=c|x,\theta )\propto \exp ({\delta }_c)$,其中:
${\delta }_c=-x^T{\beta }_c+{\gamma }_c,{\beta }_c={\hat{\Sigma }}^{-1}{\mu }_c,{\gamma }_c=-\frac{1}{2}{\mu }_c^T{\beta }_c+\log {\pi }_c$(4.62)

然后可以并不需要求逆$D\times D$矩阵就能计算正交线性判别分析(RDA)的关键项${\beta }_c$.
${\beta }_c={\hat{\Sigma }}_{map}^{-1}{\mu }_c=(V\tilde{\Sigma }{V}^{T}s{)}^{-1}{\mu }_c=V{\tilde{\Sigma }}^{-1}{V}^T{\mu }_c=V{\tilde{\Sigma }}^{-1}{\mu }_{z,c}$(4.63)

4.2.7 对角线性判别分析(Diagonal LDA)

上文所述的是正交线性判别分析(RDA),有一种简单的替代方法,就是绑定协方差矩阵(covariance matrice),即线性判别分析(LDA)中${\Sigma }_c=\Sigma$,然后对于每个类都是用一个对角协方差矩阵.这个模型就叫做对角线性判别分析模型(diagonal LDA model),等价于$\lambda =1$时候的正交线性判别分析(RDA).对应的判别函数如下所示(和等式4.33相对比一下):

${\delta }_c(x)=\log p(x,y=c|\theta )=-{\sum }_{j=1}^D\frac{(x_j-{\mu }_{cj}{)}^2}{2{\sigma }_j^2}+\log {\pi }_c$(4.64)

通常设置${\hat{\mu }}_{cj}={\bar{x}}_{cj},{\hat{\sigma }}_j^2=s_j^2$,这个$s_j^2$是特征j(跨类汇集)的汇集经验方差(pooled empirical variance).

$s_j^2=\frac{{\sum }_{c=1}^C{\sum }_{i:y_i=c}(x_{ij}-{\bar{x}}_{cj}{)}^2}{N-C}$(4.65)

对于高维度数据,这个模型比LDA和RDA效果更好(Bickel and Levina 2004).

此处查看原书图4.7

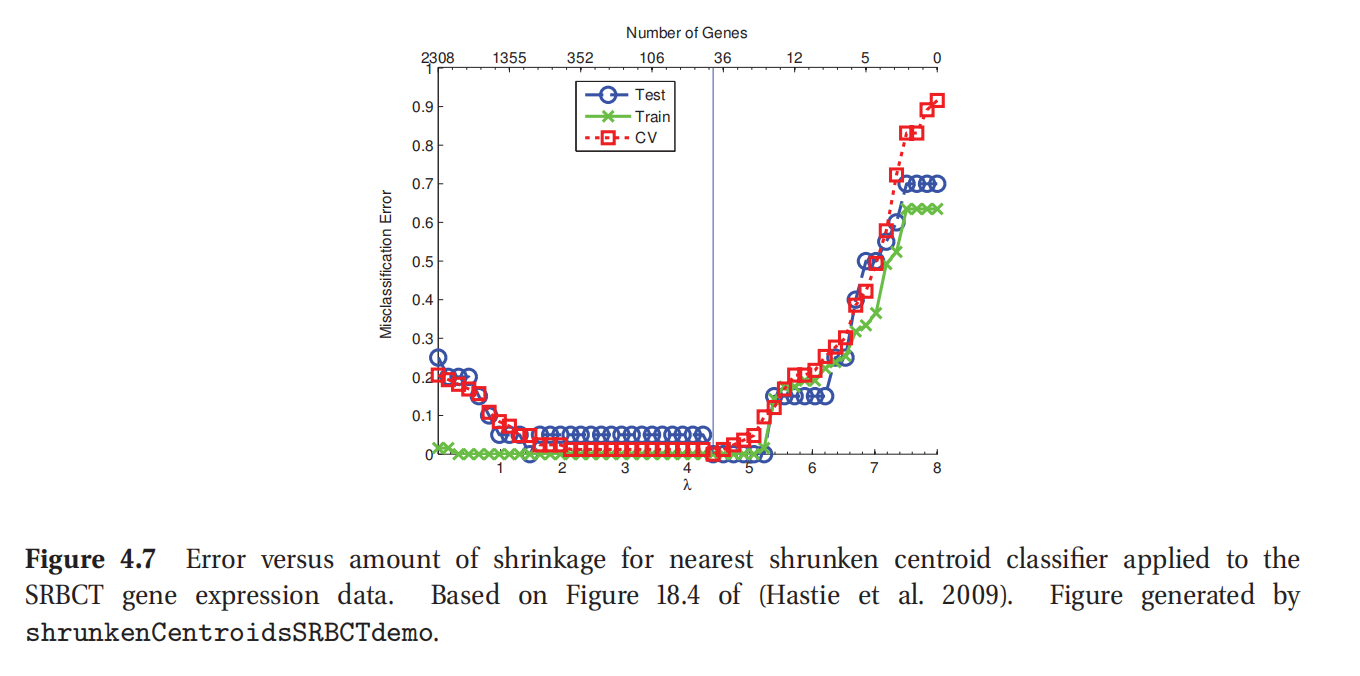
4.2.8 最近收缩质心分类器(Nearest shrunken centroids classifier)*

对角线性判别分析(diagonal LDA)有一个弱点,就是要依赖所有特征.在高维度情况下,可能更需要一个只依赖部分子集特征的方法,可以提高准确性或者利于解释.比如可以使用筛选方法(screening method),基于互信息量(mutual information),如本书3.5.4所述.本节要说另外一种方法,即最近收缩质心分类器(nearest shrunken centroids classifier, Hastie et al. 2009, p652).

基本思想是在稀疏先验(sparsity-promoting/Laplace prior)情况下对对角线性判别分析模型进行最大后验估计(MAP),参考本书13.3.更确切来说,用类独立特征均值(class-independent feature mean)$m_j$和类依赖偏移量(class-specific offset)${\Delta }_{cj}$ 来定义类依赖特征均值(class-specific feature mean)${\mu }_{cj}$。 则有:
${\mu }_{cj}=m_j+{\Delta }_{cj}$(4.66)

接下来对${\Delta }_{cj}$这一项设一个先验,使其为零,然后计算最大后验估计(MAP).对特征j,若有对于所有类别c都有${\Delta }_{cj}=0$,则该特征在分类决策中则毫无作用,因为${\mu }_{cj}$是与c独立的.这样这些不具有判别作用的特征就会被自动忽略掉.这个过程的细节可以参考 (Hastie et al. 2009, p652)和(Greenshtein and Park 2009).代码可以参考本书配套的PMTK3程序中的 shrunkenCentroidsFit.

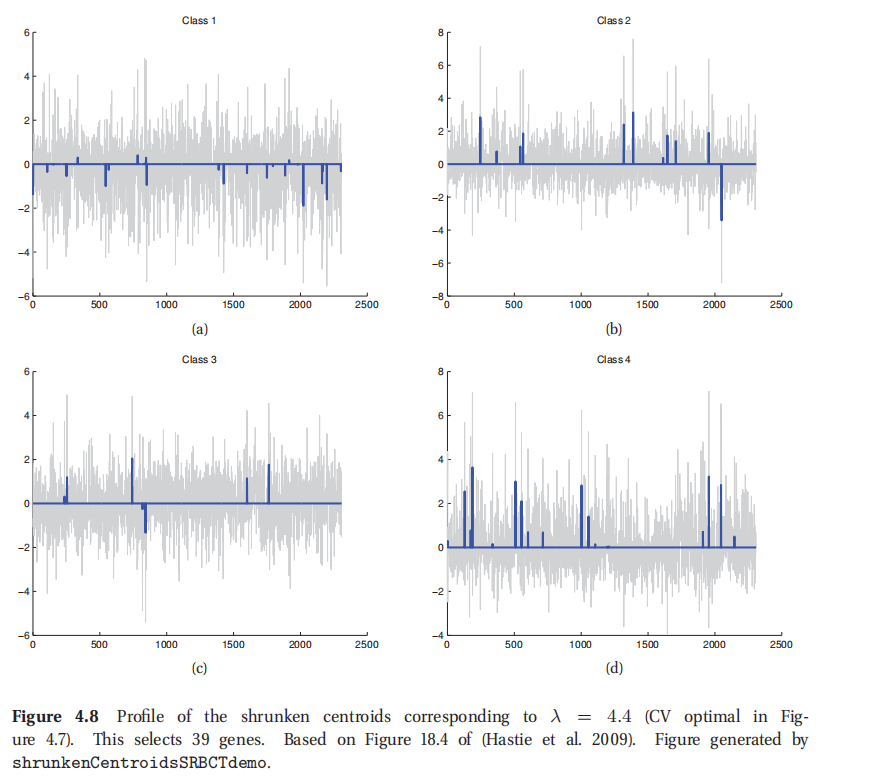
基于(Hastie et al. 2009, p652)的内容举个例子.设要对一个基因表达数据集进行分类,其中有2308个基因,4各类别,63个训练样本,20个测试样本.使用对角LDA分类器在测试集当中有五次错误.而是用最近收缩质心分类器对一系列不同的$\lambda$值,在测试集中都没有错误,如图4.7所示.更重要的是这个模型是稀疏的,所以更容易解读.图4.8所示的非惩罚估计(unpenalized estimate),灰色对应差值(difference)$d_{cj}$,蓝色的是收缩估计(shrunken estimates)${\Delta }_{cj}$.(这些估计的计算利用了通过交叉验证估计得到的$\lambda$值.)在原始的2308个基因中,只有39个用在了分类当中.

接下来考虑个更难的问题,有16,603个基因,来自144个病人的训练集,54个病人的测试集,有14种不同类型的癌症(Ramaswamy et al. 2001).Hastie 等(Hastie et al. 2009, p656) 称最近收缩质心分类器用了6520个基因,在测试集上有17次错误,而正交判别分析(RDA,本书4.3.6)用了全部的16,603个基因,在测试集上有12次错误.本书配套的PMTK3程序当中的函数cancerHighDimClassifDemo可以再现这些数字.

此处查看原书图4.8