06 Frequentist statistics

MLAPP 读书笔记 - 06 频率论统计(Frequentist statistics)

A Chinese Notes of MLAPP，MLAPP 中文笔记项目
https://zhuanlan.zhihu.com/python-kivy

转载：cycleuser

侵权立删，本意是为广大学习爱好者提供中文资料，同时在这里补充了图片，方便阅读，如果有任何法律问题，我会立即删除。

6.1 概论

第五章中讲的都是贝叶斯统计学(Bayesian statistics).贝叶斯统计学被一些人认为有争议,不过在非统计学领域,贝叶斯统计的应用却没什么争议,比如医疗诊断(本书2.2.3.1)/垃圾邮件过滤(本书3.4.4.1)/飞机追踪(本书18.2.1)等.反对者的理由与统计模型参数和其他未知量之间的区别有关.

然后就有人做出尝试,去避免把参数当作随机变量来推导统计学方法,这样就不需要使用先验和贝叶斯规则了.这种统计学就是频率论统计学(frequentist statistics),也叫经典统计学(classical statistics)或者正统统计学(orthodox statistics).这种统计学不是基于后验分布(posterior distribution),而是基于抽样分布(sampling distribution)的概念.这种分布中,估计器(estimator)在用于不同的数据集的时候,从真实的未知分布中进行抽样,具体细节参考本书6.2.重复试验的变化的概念就构成了使用频率论方法来对不确定性建模的基础.

相比之下,在贝叶斯方法中,只接受被实际观察的数据,而并没有重复测试的概念.这就允许贝叶斯方法用于计算单次事件的概率,比如在本书2.1中讲的.另一方面可能更重要,就是贝叶斯方法能避免一些困扰了频率论方法的悖论(参考本书6.6).不过总还是要熟悉一下频率论的(尤其是本书的6.5),因为这种方法在机器学习中应用也很广泛的.

6.2 一个估计器的抽样分布(Sampling distribution of an estimator)

在频率论统计学中,参数估计$\hat{\theta }$是通过对某个数据集D来使用一个估计器(estimator)$\delta$而计算得到的,也就是$\hat{\theta }=\delta (D)$.这里参数被当做固定的,而数据可以是随机的,正好和贝叶斯方法中的完全相反.参数估计的不确定性可以通过计算估计器的抽样分布(sampling distribution)来衡量.要理解这个概念,可以设想从来自某个真实模型($p(.|{\theta }^{\ast })$)的多个不同的数据集$D^{(s)}$中抽样,设 D ( s ) = { x i ( s ) } i = 1 N D^{(s)}= \{x_i^{(s)}\}^N_{i=1} D(s)={xi(s)​}i=1N​,其中$x_i^s\sim p(\ast |{\theta }^{\ast })$,而${\theta }^{\ast }$是真实参数.而$s=1:S$是对抽样数据集的索引,而N是每一个这样的数据集的规模.然后将估计器$\hat{\theta }(\ast )$用于每个$D^{(s)}$来得到一系列的估计 { θ ^ ( D ( s ) } \{\hat\theta(D^{(s)}\} {θ^(D(s)}.然后设$S\to \infty$,$\hat{\theta }(\ast )$就是估计器的抽样分布.接下来的章节中我们会介绍很多种应用这个抽样分布的方法.不过首先还是展示两种方法来计算这个抽样分布本身.

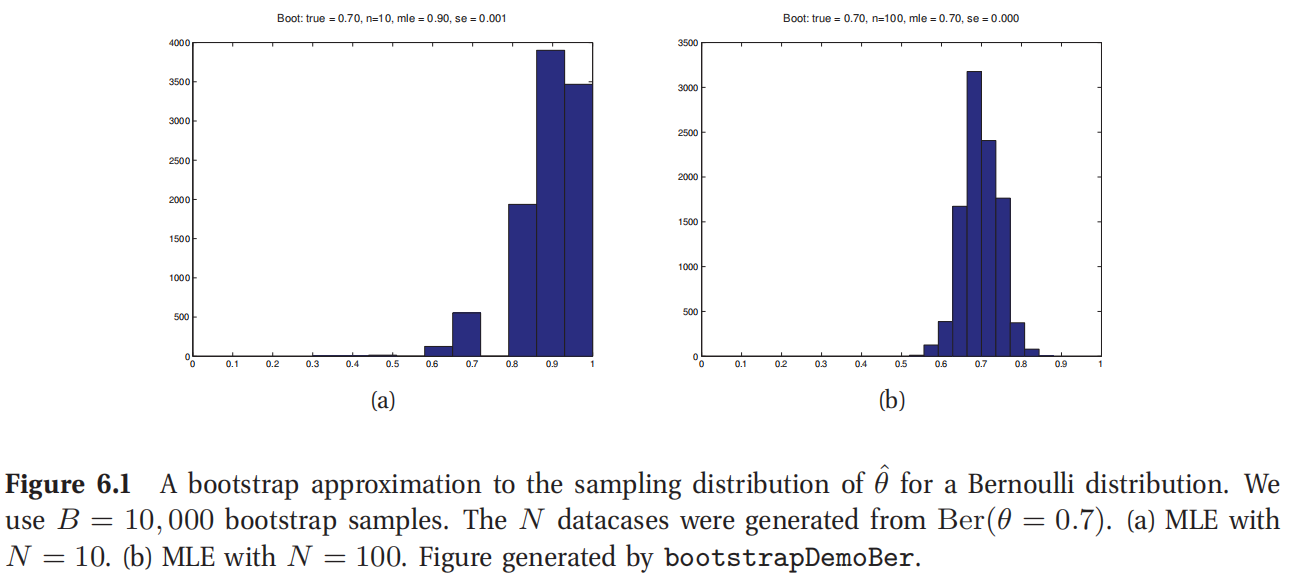
此处参考原书图6.1

6.2.1 Bootstrap

Bootstrap是一种简单的蒙特卡罗方法,来对抽样分布进行近似.在估计器是真实参数的复杂函数的情况下特别有用.

这种方法的思想很简单.如果我们知道了真实参数$\theta (\ast )$,就可以声称很多个,比如S个假的数据结构,每个规模都是N,都是来自于真实分布$x_i^s\sim p(\ast |{\theta }^{\ast })$,其中$s=1:S,i=1:N$.然后就可以从每个样本来计算估计器${\hat{\sigma }}^s=f(x_{1:N}^s)$,然后使用所得样本的经验分布作为我们对抽样分布的估计。由于$\theta$是未知的,参数化Bootstrap方法的想法是使用$\theta (D)$作为替代来生成样本.另一种方法叫非参数化的Bootstrap方法,是对$x_i^s$从原始数据D中进行可替代抽样,然后按照之前的方法计算诱导分布(induced distribution).有的方法可以在大规模数据集的场景下对Bootstrap进行加速,具体参考 (Kleiner et al. 2011).

图6.1展示了一例,其中使用了参数化Bootstrap来计算一个伯努利分布的最大似然估计(MLE)的抽样分布.(使用非参数化Bootstrap的结果本质上是相同的.)可以看到,当N=10的时候,抽样分布是不对称的,所以很不像高斯分布;而当N=100的时候,这个分布就看上去更像高斯分布了,也正如下文中所述的.

很自然的一个问题是:使用Bootstrap计算出来的参数估计器${\theta }^s=\hat{\theta }(x_{1:N}^s)$和采用后验分布抽样得到的参数值${\theta }^s\sim p(\ast |D)$有啥区别呢?
概念上两者很不一样,不过一般情况下,在先验不是很强的时候,这两者可能很相似.例如图6.1(c-d)所示就是一例,其中使用了均匀$\beta$分布$Beta(1,1)$作为先验来计算的后验,然后对其进行抽样.从图中可以看出后验和抽样分布很相似.所以有人可能就认为Bootstrap分布就可以当做是"穷人的"后验;更多内容参考(Hastie et al. 2001, p235).

然而很悲伤,Bootstrap可能会比后验取样要慢很多.原因就是Bootstrap必须对模型拟合S次,而在后验抽样中,通常只要对模型拟合一次(来找到局部众数,local mode),然后就可以在众数周围进行局部探索(local exploration).这种局部探索(local exploration)通常要比从头拟合模型快得多.

6.2.2 最大似然估计(MLE)的大样本理论(Large sample theory)

有时候有的估计器(estimator)的抽样分布可以以解析形式计算出来.比如在特定条件下,随着抽样规模趋向于无穷大,最大似然估计(MLE)的抽样分布就成了高斯分布了.简单来说,要得到这个结果,需要模型中每个参数都能"观察"到无穷多个数据量,然后模型还得是可识别的(identifiable).很不幸,这种条件是很多机器学习中常用模型都无法满足的.不过咱们还是可以假设一个简单的环境,使定理成立.

这个高斯分布的中心就是最大似然估计(MLE)$\theta$了.但方差是啥呢?直觉告诉我们这个估计器的方差可能和似然函数面(likelihood surface)的峰值处的曲率(curvature)有关(也可能是负相关).如果曲率很大,峰值那里就很陡峭尖锐,方差就小;这时候就认为这个估计确定性好(well determined).反之如果曲率很小,峰值就几乎是平的,那方差就大了去了.

咱们将这种直观感受用正规数学语言表达一下.定义一个得分函数(score function),也就是对数自然函数在某一点$\theta$处的梯度(gradient):

$s(\hat{\theta })\stackrel{△}{=}\nabla \log p(D|\theta ){|}_{\hat{\theta }}$(6.1)

把负得分函数(negative score function)定义成观测信息矩阵(observed information matrix),等价于负对数似然函数(Negative Log Likelihood,缩写为NLL)的海森矩阵(Hessian):

$J(\hat{\theta }(D))\stackrel{△}{=}-\nabla s(\hat{\theta })=-{\nabla }_{\theta }^2\log p(D|\theta ){|}_{\hat{\theta }}$(6.2)

在1维情况下,就成了:

$J(\hat{\theta }(D))=-\frac{d}{d{\theta }^2}\log p(D|\theta ){|}_{\hat{\theta }}$(6.3)

这就是对对数似然函数在点$\hat{\theta }$位置曲率的一种度量了.

由于我们要研究的是抽样分布,$D=(x_1,...,x_N)$是一系列随机变量的集合.那么费舍信息矩阵(Fisher information matrix)定义就是观测信息矩阵(observed information matrix)的期望值(expected value):

$I_N(\hat{\theta }|{\theta }^{\ast })\stackrel{△}{=}{\mathrm{E}}_{{\theta }^{\ast }}[J(\hat{\theta }|D)]$(6.4)

其中的${\mathrm{E}}_{{\theta }^{\ast }}[f(D)]\stackrel{△}{=}\frac{1}{N}{\sum }_{i=1}^{N}f(x_i)p(x_i|{\theta }^{\ast })$ 是将函数f用于从${\theta }^{\ast }$中取样的数据时的期望值.通常这个${\theta }^{\ast }$表示的都是生成数据的"真实参数",假设为已知的,所以就可以缩写出$I_N(\hat{\theta })\stackrel{△}{=}{I}_N(\hat{\theta }|{\theta }^{\ast })$.另外,还很容易就能看出$I_N(\hat{\theta })=N{I}_1(\hat{\theta })$,因为规模为N的样本对数似然函数自然要比规模为1的样本更加"陡峭(steeper)".所以可以去掉那个1的下标(subscript),然后就只写成$I_N(\hat{\theta })=I_1(\hat{\theta })$.这是常用的表示方法.

然后设最大似然估计(MLE)为$\hat{\theta }\stackrel{△}{=}{\hat{\theta }}_{mle}(D)$,其中的$D\sim {\theta }^{\ast }$.随着$N\to \infty$,则有(证明参考Rice 1995, p265)):

$\hat{\theta }\to N(({\theta }^{\ast },I_N({\theta }^{\ast }{)}^{-1})$(6.5)

我们就说这个最大似然估计(MLE)的抽样分布是渐进正态(asymptotically normal)的.

那么最大似然估计(MLE)的方差呢?这个方差可以用来衡量对最大似然估计的信心量度.很不幸,由于${\theta }^{\ast }$是未知的,所以咱们不能对抽样分布的方差进行估计.不过还是可以用$\hat{\theta }$替代${\theta }^{\ast }$来估计抽样分布.这样得到的${\hat{\theta }}_k$近似标准差(approximate standard errors)为:

${\widehat{se}}_k\stackrel{△}{=}{I}_N(\hat{\theta }{)}_{kk}^{-\frac{1}{2}}$(6.6)

例如,从等式5.60就能知道一个二项分布模型(binomial sampling model)的费舍信息(Fisher information)为:

$I(\theta )=\frac{1}{\theta (1-\theta )}$(6.7)

然后最大似然估计(MLE)的近似标准差(approximate standard error)为:

$\widehat{se}=\frac{1}{\sqrt{I_N(\hat{\theta })}}=\frac{1}{\sqrt{NI(\hat{\theta })}}=(\frac{\hat{\theta }(1-\hat{\theta })}{N}{)}^{\frac{1}{2}}$(6.8)

其中$\hat{\theta }=\frac{1}{N}{\sum }_i{X}_i$.可以对比等式3.27,即均匀先验下的后验标准偏差(posterior standard deviation).

6.3 频率论决策理论(Frequentist decision theory)

在频率论或者经典决策理论中,有损失函数和似然函数,但没有先验,也没有后验,更没有后验期望损失(posterior expected loss)了.因此和贝叶斯方法不同,频率论方法中没有办法来自动推导出一个最优估计器.在频率论方法中,可以自由选择任意的估计器或者决策规则$\delta :X\to A$.
选好了估计器,就可以定义对应的期望损失(expected loss)或者风险函数(risk),如下所示:
$R({\theta }^{\ast },\delta )\stackrel{△}{=}{\mathrm{E}}_{p(\tilde{D}|{\theta }^{\ast })}[L({\theta }^{\ast },\delta (\tilde{D}))=\int L({\theta }^{\ast },\delta (\tilde{D}))p(\tilde{D}|{\theta }^{\ast })d\tilde{D}]$(6.9)

上式中的$\tilde{D}$是从"自然分布(nature’s distribution)"抽样的数据,用参数${\theta }^{\ast }$来表示.也就是说,期望值是估计量大抽样分布相关的.可以和贝叶斯后验期望损失(Bayesian posterior expected loss:)相比:

$\rho (a|D,\pi )\stackrel{△}{=}\mathrm{E}[L(\theta ,a)]={\int }_{\Theta }L(\theta ,a)p(\theta |D,\pi )d\theta$(6.10)

很明显贝叶斯方法是在位置的$\theta$上进行平均,条件为已知的D,而频率论方法是在$\tilde{D}$上平均,(也就忽略了观测值),而条件是未知的${\theta }^{\ast }$.

这种频率论的定义不光看着很不自然,甚至根本就没办法计算,因为${\theta }^{\ast }$都不知道.结果也就不能以频率论的风险函数(frequentist risk)来对比不同的估计器了.接下来就说一下对这个问题的解决方案.

6.3.1 贝叶斯风险

怎么挑选估计器呢?我们需要把$R({\theta }^{\ast },\delta )$转换成一个不需要依赖${\theta }^{\ast }$的单独量$R(\delta )$.一种方法是对${\theta }^{\ast }$设一个先验,然后定义一个估计器的贝叶斯风险(Bayes risk)或者积分风险(integrated risk),如下所示:

$R_B(\delta )\stackrel{△}{=}{\mathrm{E}}_{p({\theta }^{\ast })}[R({\theta }^{\ast },\delta )]=\int R({\theta }^{\ast },\delta )p({\theta }^{\ast })d{\theta }^{\ast }$(6.11)

贝叶斯估计器(Bayes estimator)或者贝叶斯决策规则(Bayes decision rule)就是将期望风险最小化:
$\delta_B \overset{\triangle}{=} \arg\min_\delta R_B(\delta) $(6.12)

要注意这里的积分风险函数(integrated risk)也叫做预制后验风险(preposterior risk),因为是在看到数据之前得到的.对此最小化有助于实验设计.

接下来有一个重要定理,这个定理将贝叶斯方法和频率论方法一起结合到了决策理论中.

定理6.31

贝叶斯估计器可以通过最小化每个x的后验期望损失(posterior expected loss)而得到.

证明.切换积分顺序,就有:
$$\begin{array}{rlr}{R}_B(\delta )& =\int [\sum _x\sum _{y}L(y,\delta (x))p(x,y|{\theta }^{\ast })]p({\theta }^{\ast })d{\theta }^{\ast }& \text{(6.13)}\\ & \sum _x\sum _y{\int }_{\Theta }L(y,\delta (x))p(x,y,{\theta }^{\ast })d{\theta }^{\ast }& \text{(6.14)}\\ & =\sum _x[\sum _{y}L(y,\delta (x))p(y|x)dy]p(x)& \text{(6.15)}\\ & =\sum _x\rho (\delta (x)|x)p(x)& \text{(6.16)}\end{array}$$

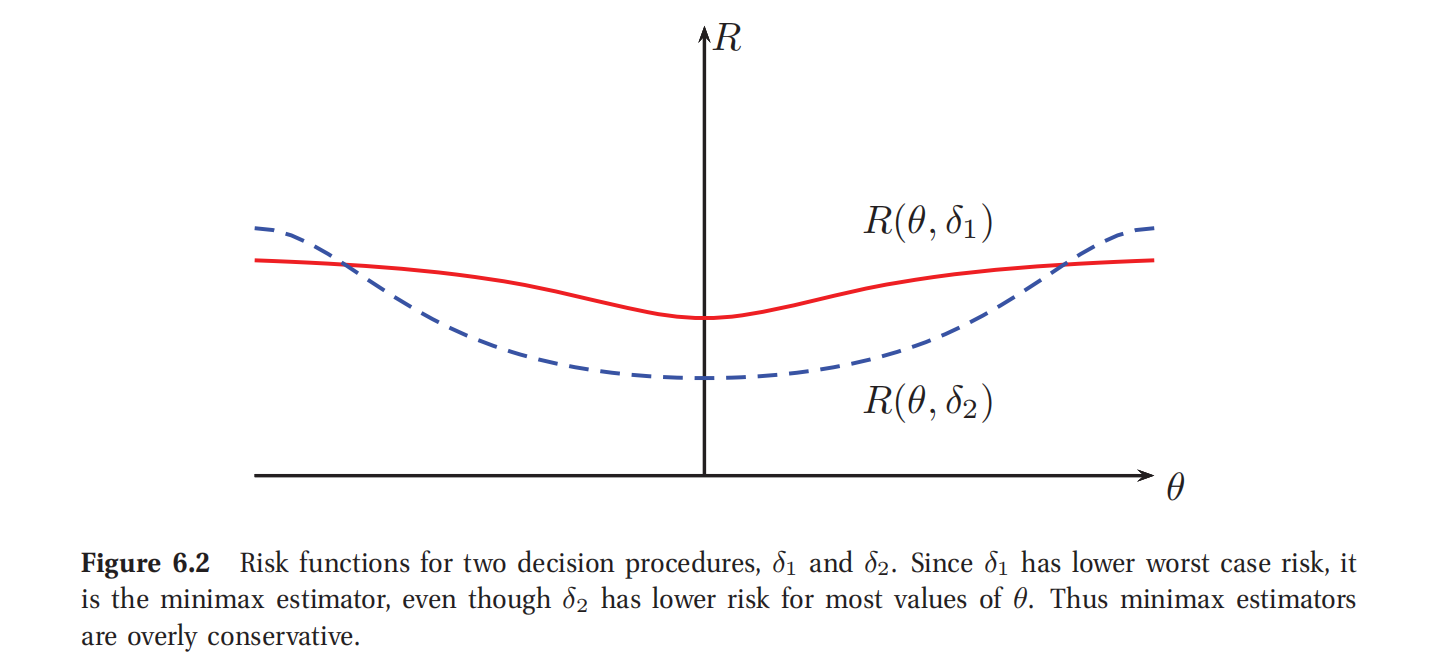
此处参考原书图6.2

要最小化全局期望(overall expectation),只要将每个x项最小化就可以了,所以我们的决策规则就是要挑选:

$\delta_B (x)=\arg\min_{a\in A} \rho(a|x) $(6.17)
证明完毕.

定理6.32 (Wald,1950)

每个可接受的决策规则都是某种程度上的贝叶斯决策规则,对应着某些可能还不适当的先验分布.
这就表明,对频率论风险函数最小化的最佳方法就是贝叶斯方法!更多信息参考(Bernardo and Smith 1994, p448).

6.3.2 最小最大风险(Minimax risk)

当然咯,很多频率论者不喜欢贝叶斯风险,因为这需要选择一个先验(虽然这只是对估计器的评估中要用到,并不影响估计器的构建).所以另外一种方法就如下所示.定义一个估计器的最大风险如下所示:

$R_{max}(\delta )\stackrel{△}{=}{\max }_{{\theta }^{\ast }}R({\theta }^{\ast },\delta )$(6.18)

最小最大规则(minimax rule)就是将最大风险最小化:
${\delta }_{MM}\stackrel{△}{=}\arg {\min }_{\delta }{R}_{max}(\delta )$(6.19)

例如图6.2中,很明显在所有的${\theta }^{\ast }$值上,${\delta }_1$有比${\delta }_2$更低的最差情况风险(lower worst-case risk),所以就是最小最大估计器(关于如何计算一个具体模型的风险函数的解释可以参考本书6.3.3.1).

最小最大估计器有一定的吸引力.可惜,计算过程可难咯.而且这些函数还都很悲观(pessimistic).实际上,所有的最小最大估计器都是等价于在最不利先验下的贝叶斯估计器.在大多数统计情境中(不包括博弈论情境),假设自然充满敌意并不是一个很合理的假设.

6.3.3 可容许的估计器(Admissible estimators)

频率论决策理论的基本问题就是要知道真实分布$p(\ast |{\theta }^{\ast })$才能去评估风险.可是有的估计器可能不管${\theta }^{\ast }$是什么值,都会比其他的一些估计器更差.比如说,如果对于所有的$\theta \in \Theta$,都有$R(\theta ,{\delta }_1)<R(\theta ,{\delta }_2)$,那么就说${\delta }_1$支配了${\delta }_2$.如果不等关系对于某个$\theta$来说严格成立,就说这种支配关系是严格的.如果一个估计器不被另外的估计器所支配,就说这个估计器是可容许的(Admissible).

6.3.3.1 样例

这个例子基于(Bernardo and smith 1994).这个问题是去估计一个正态分布的均值.假设数据样本抽样自一个正态分布$x_i\sim N({\theta }^{\ast },{\sigma }^2=1)$,然后使用平方损失函数(quadratic loss)$L(\theta ,\hat{\theta })=(\theta -\hat{\theta }{)}^2$.这时候对应的风险函数就是均方误差(MSE).估计器$\hat{\theta }(x)=\delta (x)$也就是一些可能的决策规则,如下所示:

• ${\delta }_1(x)=\bar{x}$,这个是样本均值
• ${\delta }_2(x)=\tilde{x}$,这个是样本中位数
• ${\delta }_3(x)={\theta }_0$,这个是某个固定值
• ${\delta }_k(x)$,这个是在先验$N(\theta |{\theta }_0,{\sigma }^2/k)$下的后验均值:
  ${\delta }_k(x)=\frac{N}{N+k}\bar{x}+\frac{k}{N+k}{\theta }_0=w\bar{x}+(1-w){\theta }_0$(6.20)

对${\delta }_k$可以设置一个弱先验$k=1$,以及一个更强的先验$k=5$.先验均值是某个固定值${\theta }_0$.然后假设${\sigma }^2$已知.(这样${\delta }_3(x)$就和${\delta }_k(x)$一样了,后者有一个无穷强先验$k=\infty$.)

接下来就以解析形式来推导风险函数了.(在这个样例中可以这么做,是因为已经知道了真实参数${\theta }^{\ast }$.)在本书6.4.4,会看到均方误差(MES)可以拆解成平方偏差(squared bias)加上方差(variance)的形式:
$MSE(\hat{\theta }(\ast )|pthet{a}^{\ast }=var[\hat{\theta }]+bia{s}^2(\hat{\theta })$(6.21)

样本均值是没有偏差的(unbiased),所以其风险函数为:
$MSE(\delta_1|\theta^*) =var[\bar x]=\frac{\sigma^2}{N} $(6.22)

此处参考原书图6.3

样本中位数也是无偏差的.很明显其方差大约就是$\pi /(2N)$,所以有:

$MSE({\delta }_2|{\theta }^{\ast })=\frac{\pi }{2N}$(6.23)

对于固定值的${\delta }_3(x)={\theta }_0$,方差是0,所以有:

$MSE({\delta }_3|{\theta }^{\ast })=({\theta }^{\ast }-{\theta }_0{)}^2$(6.24)

最后是后验均值,如下所示:

$$\begin{array}{rlr}MSE({\delta }_k|{\theta }^{\ast })& =\mathrm{E}[(w\bar{x}+(1-w){\theta }_0-{\theta }^{\ast }{)}^2]& \text{(6.25)}\\ & =\mathrm{E}[(w(\bar{x}-{\theta }^{\ast })+(1-w)({\theta }_0-{\theta }^{\ast }){)}^2]& \text{(6.26)}\\ & =w^2\frac{{\sigma }^2}{N}+(1-w{)}^2({\theta }_0-{\theta }^{\ast }{)}^2& \text{(6.27)}\\ & =\frac{1}{(N+k{)}^2}(N{\sigma }^2+k^2({\theta }_0-{\theta }^{\ast }{)}^2)& \text{(6.28)}\end{array}$$

图6.3中所示是在 N ∈ { 5 , 20 } N\in \{5,20\} N∈{5,20}范围内的上面几个函数的图像.可以看出总体上最佳的估计器都是依赖${\theta }^{\ast }$值的那几个,可是${\theta }^{\ast }$还是未知的.如果${\theta }^{\ast }$很接近${\theta }_0$,那么${\delta }_3$(实际上就是预测的${\theta }_0$)就是最好的了.如果${\theta }^{\ast }$在${\theta }_0$范围内有一定波动,那么后验均值,结合了对${\theta }_0$的猜测和数据所反映的信息,就是最好的.如果${\theta }^{\ast }$远离${\theta }_0$,那么最大似然估计(MLE)就是最好的.这也一点都不让人意外:假设先验均值敏感,小规模的收缩(shrinkage)是通常期望的(使用一个弱先验的后验均值).

令人意外的是对于任意的${\theta }_0$值,决策规则${\delta }_2$(样本中位数)的风险函数总是比${\delta }_1$(样本均值)的风险函数更大.也就是说,样本中位数对于这个问题来说是一个不可容许估计器(inadmissible estimator)(这个问题是假设数据抽样自一个正态分布).

可是在实践中,样本中位数其实往往比样本均值更好,因为对于异常值不敏感,更健壮.参考(Minka 2000d)可知,如果假设数据来自于比高斯分布(正态分布)更重尾(heavier tails)的拉普拉斯分布(Laplace distribution),那么样本中位数就是贝叶斯估计器(Bayes estimator)(使用平方损失函数(squared loss)).更一般地,可以对数据使用各种灵活的模型来构建健壮的估计器,比如混合模型,或者本书14.7.2会讲到的非参数化密度估计器(non-parametric density estimators),然后再去计算后验均值或者中位数.

6.3.3.2 斯坦因悖论(Stein’s paradox)*

加入有N个独立同分布(iid)随机变量服从正态分布,即$X_i\sim N({\theta }_i,1)$,然后想要估计${\theta }_i$.很明显估计器应该用最大似然估计(MLE)这时候就是设${\hat{\theta }}_i=x_i$.结果表明:$N\ge 4$的时候,这是一个不可容许估计器(inadmissible estimator).

怎么证明?构建一个更好的估计器就可以了.比如吉姆斯-斯坦因估计器(James-Stein estimator)就可以,定义如下所示:

${\hat{\theta }}_i=\hat{B}\bar{x}+(1-\hat{B})(x_i-\bar{x})$(6.29)

上式中的$\bar{x}=\frac{1}{N}{\sum }_{i=1}^N{x}_i$,而$0<B<1$是某个调节常数.这个估计其会将${\theta }_i$朝向全局均值进行收缩(shrink).(在本书5.6.2使用经验贝叶斯方法推导过这个估计器.)

很明显,当$N\ge 4$的时候,这个收缩估计器比最大似然估计(MLE,也就是样本均值)有更低的频率风险(均方误差MSE).这就叫做斯坦因悖论(Stein’s paradox).为啥说这是个悖论呢?这就解释一下.假如${\theta }_i$是某个学生i的真实智商值(IQ),而$X_i$是其测试分数.为啥用全局均值来估计特定的${\theta }_i$,用其他学生的分数去估计另一个学生的分数?利用不同范畴的东西还可以制造更加荒诞的自相矛盾的例子,比如加入${\theta }_1$是我的智商,而${\theta }_2$是温哥华平均降雨量,这有毛线关系?

这个悖论的解决方案如下所述.如果你的目标只是估计${\theta }_i$,那么用$x_i$来估计就已经是最好的选择了,可是如果你的目的是估计整个向量$\theta$,而且你还要用平方误差(squared error)作为你的损失函数,那么那个收缩估计器就更好.为了更好理解,假设我们要从一个单一样本$x\sim N(\theta ,I)$来估计$||\theta |{|}_2^2$.最简单的估计就是$||x|{|}_2^2$,不过会遇到上面的问题,因为:

$\mathrm{E}[||x|{|}_2^2]=\mathrm{E}[{\sum }_i{x}_i^2]={\sum }_{i=1}^N(1+{\theta }_i^2)=N+||\theta |{|}_2^2$(6.30)

结果就需要增加更多信息来降低风险,而这些增加的信息可能甚至来自于一些不相关的信息源,然后估计就会收缩到全局均值上面了.在本书5.6.2对此给出过贝叶斯理论的解释,更多细节也可以参考(Efron and Morris 1975).

6.3.3.3 可容许性远远不够(Admissibility is not enough)

从前文来看,似乎很明显我们应该在可容许估计器范围内来搜索好的估计器.但实际上远不止构建可容许估计器这么简单,比如接下来这个例子就能看出.

定理 6.3.3

设有正态分布$X\sim N(\theta ,1)$,在平方误差下对$\theta$进行估计.设${\delta }_1(x)={\theta }_0$是一个独立于数据的常量.这是一个可容许估计器(admissible estimator).

证明:用反证法,假设结论不成立,存在另外一个估计器${\delta }_2$有更小风险,所以有$R({\theta }^{\ast },{\delta }_2)\le R({\theta }^{\ast },{\delta }_1)$,对于某些${\theta }^{\ast }$不等关系严格成立.设真实参数为${\theta }^{\ast }={\theta }_0$.则$R({\theta }^{\ast },{\delta }_1)=0$,并且有:

$R({\theta }^{\ast },{\delta }_2)=\int ({\delta }_2(x)-{\theta }_0{)}^{2}p(x|{\theta }_0)dx$(6.31)

由于对于所有的${\theta }^{\ast }$都有$0\le R({\theta }^{\ast },{\delta }_2)\le R({\theta }^{\ast },{\delta }_1)$,而$R({\theta }_0,{\delta }_1)=0$,所以则有$R({\theta }_0,{\delta }_2)=0,{\delta }_2(x)={\theta }_0={\delta }_1(x)$.这就表明了${\delta }_2$只有和${\delta }_1$相等的情况下才能避免在某一点${\theta }_0$处有更高风险.也就是说不能有其他的估计器${\delta }_2$能严格提供更低的风险.所以${\delta }_1$是可容许的.证明完毕

6.4 估计器的理想性质

由于频率论方法不能提供一种自动选择最佳估计器的方法,我们就得自己想出其他启发式的办法来进行选择.在本节,就讲一下我们希望估计器所具有的一些性质.不过很不幸,我们会发现这些性质不能够同时满足.

6.4.1 连续估计器(Consistent estimators)

连续估计器,就是随着取样规模趋近于无穷大,最终能够恢复出生成数据的真实参数的估计器,也就是随着$|D|\to \infty$,$\hat{\theta }(D)\to {\theta }^{\ast }$(这里的箭头指的是概率收敛的意思).当然了,这个概念要有意义,就需要保证数据确实是来自某个具有参数${\theta }^{\ast }$的特定模型,而现实中这种情况很少见的.不过从理论上来说这还是个很有用的性质.

最大似然估计(MLE)就是一个连续估计器.直观理解就是因为将似然函数最大化其实就等价于将散度$KL(p(\ast |{\theta }^{\ast })||p(\ast |\hat{\theta }))$最小化,其中的$p(\ast |{\theta }^{\ast })$是真实分布,而$p(\ast |\hat{\theta })$是估计的.很明显当且仅当$\hat{\theta }={\theta }^{\ast }$的时候才有0散度(KL divergence).

6.4.2 无偏差估计器(Unbiased estimators)

估计器的偏差(bias)定义如下:

$bias(\hat{\theta }(\ast ))={\mathrm{E}}_{p(D|{\theta }_{\ast })}[\hat{\theta }(D)-{\theta }_{\ast }]$(6.32)

上式中的${\theta }_{\ast }$就是真实的参数值.如果偏差为0,就说这个估计器无偏差.这意味着取样分布的中心正好就是真实参数.例如对于高斯分布均值的最大似然估计(MLE)就是无偏差的:

$\mathrm{bias}(\hat{\mu })=\mathbb{E}\left[\overline{x}\right]-\mu =\mathbb{E}\left[\frac{1}{N}{\sum }_{i=1}^N{x}_i\right]-\mu =\frac{N\mu }{N}-\mu =0$

不过对高斯分布方差${\hat{\sigma }}^2$的最大似然估计(MLE)就不是对${\sigma }^2$的无偏估计.实际上可以发现(参考练习6.3):

$\mathrm{E}[{\hat{\sigma }}^2]=\frac{N-1}{N}{\sigma }^2$(6.34)

不过下面这个估计器就是一个无偏差估计器:

${\hat{\sigma }}_{N-1}^2=\frac{N}{N-1}{\hat{\sigma }}^2=\frac{1}{N-1}{\sum }_{i=1}^N(x_i-\bar{x}{)}^2$(6.35)

对上式,可以证明有:

$\mathrm{E}[{\hat{\sigma }}_{N-1}^2]=\mathrm{E}[\frac{N}{N-1}{\sigma }^2]=\frac{N}{N-1}\frac{N-1}{N}{\sigma }^2={\sigma }^2$(6.36)

在MATLAB中,$var(X)$返回的就是,${\hat{\sigma }}_{N-1}^2$而$var(X,1)$返回的是最大似然估计(MLE)${\sigma }^2$.对于足够大规模的N,这点区别就可以忽略了.

虽然最大似然估计(MLE)可能有时候有偏差,不过总会逐渐无偏差.(这也是最大似然估计(MLE)是连续估计器的必要条件.)

虽然无偏听上去好像是个很理想的性质,但也不总是好事,更多细节可以参考本书6.4.4以及(Lindley 1972)的相关讨论.

6.4.3 最小方差估计器

直观来看,好像让估计器尽量无偏差是很合理的(不过后面我们会看到事实并非如此简单).不过只是无偏还不够用.比如我们想要从集合 D = { x 1 , . . , x N } D=\{x_1,..,x_N\} D={x1​,..,xN​}估计一个高斯均值.最开始对第一个数据点用这个估计器的时候$\hat{\theta }(D)=x_1$,这时候还是无偏估计,但逐渐就会比经验均值$\bar{x}$(这也是无偏的)更远离真实的${\theta }_{\ast }$.所以一个估计器的方差也很重要.

很自然的问题:方差能到多大?有一个著名的结论,叫做克莱默-饶下界(Cramer-Rao lower bound)为任意的无偏估计器的方差提供了下界.具体来说如下所示:

定理6.4.1 (克莱默-饶 不等式)

设 $X_1,..,X_n\sim p(X|{\theta }_0)$,而$\hat{\theta }=\hat{\theta }(x_1,..,x_n)$是一个对参数${\theta }_0$的无偏估计器.然后在对$p(X|{\theta }_0)$的各种平滑假设下,有:

$var[\hat{\theta }]\ge \frac{1}{nI({\theta }_0)}$(6.37)

其中的$I({\theta }_0)$是费舍信息矩阵(Fisher information matrix)(参考本书6.2.2).

对此的证明可以参考(Rice 1995, p275).
可以证明最大似然估计(MLE)能达到克莱默-饶下界,因此对于任意无偏估计器都会有渐进的最小方差.所以说最大似然估计(MLE)是渐进最优(asymptotically optimal)的.

6.4.4 偏差-方差权衡

使用无偏估计看上去是个好主意,实际并非如此简单.比如用一个二次损失函数为例.如上文所述,对应的风险函数是均方误差(MSE).然后我们能推出一个对均方误差(MSE)的有用分解.(所有期望和方差都是关于真实分布$p(D|{\theta }^{\ast })$,但为了表达简洁,这里就把多余的条件都舍掉了.)设$\hat{\theta }=\hat{\theta }(D)$表示这个估计,然后$\bar{\theta }=\mathrm{E}[\hat{\theta }]$表示的是估计的期望值(变化Ｄ来进行估计)．然后就有：

$\begin{array}{rl}\mathbb{E}\left[(\hat{\theta }-{\theta }^{\ast }{)}^2\right]& =\mathbb{E}\left[{\left[(\hat{\theta }-\overline{\theta })+(\overline{\theta }-{\theta }^{\ast })\right]}^2\right]\\ & \begin{array}{rl}=& \mathbb{E}\left[{\left(\hat{\theta }-\overline{\theta }\right)}^2\right]+2(\overline{\theta }-{\theta }^{\ast })\mathbb{E}\left[\hat{\theta }-\overline{\theta }\right]+(\overline{\theta }-{\theta }^{\ast }{)}^2\end{array}\\ & =\mathbb{E}\left[{\left(\hat{\theta }-\overline{\theta }\right)}^2\right]+(\overline{\theta }-{\theta }^{\ast }{)}^2\\ & =\mathrm{var}\left[\hat{\theta }\right]+{\mathrm{bias}}^2(\hat{\theta })\end{array}$

用文字表达就是：

$MSE=variance+bia{s}^2$(6.42)重要公式

这也就是偏差－方差之间的权衡（bias-variance tradeoff），可以参考(Geman et al. 1992)．这就意味着假设我们的目标是要最小化平方误差，那么选择一个有偏差估计器也可能是可取的，只要能够降低方差．

6.4.4.1 样例:估计高斯均值

然后举个例子吧，基于(Hoff 2009, p79).假如要从$x=(x_1,..,x_N)$估计高斯均值.架设数据采样自一个正态分布$x_i\sim N({\theta }^{\ast }=1,{\sigma }^2)$.很明显可以用最大似然估计(MLE).这样估计器偏差为0,方差为:

$var[\bar{x}|{\theta }^{\ast }]=\frac{{\sigma }^2}{N}$(6.43)

不过也可以使用最大后验估计(MAP estimate).在本书4.6.1中,我们已经遇到过使用正态分布$N({\theta }_0,{\sigma }^2/K_0)$先验的最大后验估计为:

$\tilde{x}\stackrel{△}{=}\frac{N}{N+k_0}\bar{x}+\frac{k_0}{N+k_0}{\theta }_0=w\bar{x}+(1-w){\theta }_0$(6.44)

其中$0\le w\le 1$控制了我们对最大似然估计(MLE)相比先验的信任程度.(这也是后验均值,因为高斯分布的均值和众数相等.)偏差和方差为:

$\begin{array}{rcl}\mathbb{E}\left[\tilde{x}\right]-{\theta }^{\ast }& =& w{\theta }_0+(1-w){\theta }_0-{\theta }^{\ast }=(1-w)({\theta }_0-{\theta }^{\ast })\\ \mathrm{var}\left[\tilde{x}\right]& =& w^2\frac{{\sigma }^2}{N}\end{array}$

此处参考原书图6.4

虽然最大后验估计有偏差(设 w<1),但方差更低.

假设先验有些错误,所以使用${\theta }_0=0$,而真实的${\theta }^{\ast }=1$.如图6.4(a)所示,可以看到对$k_0>0$的最大后验估计的抽样分布是偏离于真实值的,但方差比最大似然估计(MLE)的更低(也就是更窄).

如图6.4(b)所示是$mse(\tilde{x})/mse(\bar{x})$对 N 的函数曲线.可见最大后验估计(MAP)比最大似然估计(MLE)有更低的均方误差(MSE),尤其是样本规模小的时候,比如 k 0 ∈ { 1 , 2 } k_0\in \{1,2\} k0​∈{1,2}.$k_0=0$的情况对应的就是最大似然估计(MLE),而$k_0=3$对应的就是强先验,这就会影响性能了,因为先验均值是错的.很明显,对先验强度的调整很重要,后面会讲到.

6.4.4.2 样例:岭回归(ridge regression)

在偏差方差之间进行权衡的另外一个重要例子就是岭回归(ridge regression),我们会在本书7.5讲到.简单来说,对应的就是在高斯先验$p(w)=N(w|0,{\lambda }^{-1}I$下对线性回归(linear regression)的最大后验估计(MAP).零均值先验使得先验的权值很小,也就降低了过拟合的概率;精度项$\lambda$控制了先验的强度.设置$\lambda =0$就是最大似然估计(MLE);使用$\lambda >0$就得到了一个有偏差估计.要展示方差的效果,可以考虑一个简单的例子.比如图6.5左边的就是每个拟合曲线的投图,右边的是平均的拟合曲线.很明显随着归一化强度的增加,方差降低了,但是偏差增大了.

此处参考原书图6.5

6.4.4.3 对于分类的偏差-方差权衡

如果使用0-1损失函数,而不是用平方损失,上面的分析就不适合了,因为频率论的风险函数不再能表达成平方偏差加上方差的形式了.实际上可以发现(参考练习7.2(Hastie et al. 2009)):偏差和方差是以相乘方式结合起来的(combine multiplicatively).如果估计结果处于决策边界的正确一侧,偏差就是负的,然后降低方差就可以降低误分类率.但如果估计位于决策边界的错误一侧,那么偏差就是正的,就得增加方差(Friedman 1997a).这就表明对于分类来说,偏差方差权衡没多大用.最好还是关注到期望损失(expected loss)上,而不是直接关注偏差和方差.可以使用交叉验证来估计期望损失,具体会在本书6.5.3中讲到.

6.5 经验风险最小化(Empirical risk minimization)

频率论决策方法难以避免的一个基本问题就是不能计算出风险函数,因为要知道真实数据分布才行.(作为对比,贝叶斯后验期望损失就总能计算出来,因为条件是在数据上的,而不是真实参数${\theta }^{\ast }$.)不过也有个办法能避免这个问题,也就是要预测已观测量,而不是估计隐藏变量或者隐藏参数.也就是不以$L(\theta ,\delta (D))$的形式来找损失函数(其中的$\theta$是未知的真实参数,而$\delta (D)$是估计器),而是以$L(y,\delta (x))$形式来找损失函数,其中的y是未知的真实响应变量(response),而$\delta (x)$是对给定的输入特征x做出的预测.这样一来,频率论的风险函数就是:

$R(p_{\ast },\delta \stackrel{△}{=}{\mathrm{E}}_{(x,y)\sim p_{\ast }}[L(y,\delta (x)]={\sum }_x{\sum }_{y}L(y,\delta (x))p_{\ast }(x,y)$(6.47)

上式中的$p_{\ast }$表示的是真实的自然分布.当然这个分布是未知的,不过可以使用一个经验分布来近似,这个经验分布是通过训练及数据来得到:

$p_{\ast }(x,y)\approx p_{emp}(x,y)\stackrel{△}{=}\frac{1}{N}{\sum }_{i]1}^N{\delta }_{x_i}(x){\delta }_{y_i}(y)$(6.48)

然后可以定义经验风险(empirical risk):

$R_{emp}(D,D)\stackrel{△}{=}R(P_{emp},\delta =\frac{1}{N}{\sum }_{i=1}^{N}L(y_i,\delta (x_i))$(6.49)

在0-1损失函数的情况下,上面的$L(y,\delta (x))=I(y\ne \delta (x))$,上面这个经验风险就成了误分类率(misclassification rate)了.在平方误差损失函数的情况下,上式中的$L(y,\delta (x))=(y-\delta (x){)}^2$,这就成了均方误差(mean squared error).然后定义经验风险最小化(empirical risk minimization, 缩写为ERM),就是找到一个能使经验风险最小化的决策过程(通常都是分类规则):

${\delta }_{ERM}(D)=\arg {\min }_{\delta }{R}_{emp}(D,\delta )$(6.50)

在无监督学习的情况下,可以去掉所有带y的项目,然后将$L(y,\delta (x))$替换成$L(x,\delta (x))$,比如,设$L(x,\delta (x))=||x-\delta (x)|{|}_2^2$,衡量的是重建误差(reconstruction error).然后使用$\delta (x)=decode(encode(x))$定义决策规则,就类似向量量化(vector quantization,参考本书11.4.2.6)和主成分分析(principal component analysis,缩写为PCA,本书12.2).最后就得到了经验风险函数的定义形式如下:

$R_{emp}(D,\delta )=\frac{1}{N}{\sum }_{i=1}^{N}L(x_i,\delta (x_i))$(6.51)

当然了,总还可以设置$\delta (x)=x$来最小化风险,所以对于解码编码来说,某些瓶颈都很关键.

6.5.1 规范化风险最小化(Regularized risk minimization)

要注意,如果对"自然分布"的先验严格等于经验分布,那么贝叶斯风险就和经验风险相等了(Minka 2001b):

$\mathrm{E}[R(p_{\ast },\delta )|p_{\ast }=p_{emp}]=R_{emp}(D,\delta )$(6.52)

因此最小化经验风险,就可能导致过拟合.所以通常都得为目标函数增加一个复杂度惩罚函数(complexity penalty):

$R"(D,\delta )=R_{emp}(D,\delta )+\lambda C(\delta )$(6.53)

上式中的$C(\delta )$衡量的是预测函数$\delta (x)$的复杂度,而$\lambda$控制的是复杂度惩罚的程度.这个方法就叫做规范风险最小化(regularized risk minimization,缩写为RRM).要注意如果损失函数是对数似然函数的负数,那么规范化项(regularizer)就是负的对数先验,这也就等价于最大后验估计(MAP).

规范化风险最小化(RRM)有两个关键问题:如何衡量复杂度,以及如何挑选$\lambda$.对于线性模型来说,可以用其自由度定义成复杂度,具体细节参考本书7.5.3.更多的通用模型,可以使用VC维度(VC dimension),参考本书6.5.4.要挑选$\lambda$,可以使用在6.5.2中要讲到的方法.

6.5.2 结构风险最小化

规范化风险最小化原则表明,对于给定的复杂度惩罚函数(complexity penalty),可以使用下面的公式来拟合模型:

${\hat{\delta }}_{\lambda }=\arg {\min }_{\delta }[R_{emp}(D,\delta )+\lambda C(\delta )]$(6.54)

可是要怎么选择$\lambda$?不能使用训练集,因为这会低估真实风险,也就是所谓的训练误差优化(optimism of the training erro)问题.或者也可以使用下面的规则,也就是结构风险最小化(structural risk minimization)原则(Vapnik 1998):

$\hat\lambda =\arg\min_{\lambda} \hat R(\hat \delta _{\lambda}) $(6.55)

上式中的$\hat{R}(\delta )$是对风险的估计.有两种广泛应用的估计:交叉验证,以及风险理论上界约束.接下来两种都讲一下.

6.5.3 使用交叉验证估计风险函数

可以利用一个验证集来估计某个估计器的风险.如果没有单独的验证集,可以使用交叉验证(cross validation,缩写为CV),在本书1.4.8中已经简单讲过了.更确切来说,交叉验证定义如下.设训练集中有$N=|D|$个数据.将第k份数据表达为$D_k$,而其他的所有数据就表示为$D_{-k}$.(在分层交叉验证(stratified CV)中,如果类标签是离散的,就选择让每份数据规模都基本相等.)然后设F是一个学习算法或者拟合函数,使用数据集D,并且模型索引为m(这个可以使离散索引,比如多项式指数,也可以是连续的,比如规范化强度等等),然后返回的就是参数向量:

${\hat{\theta }}_m=F(D,m)$(6.56)

最后,设P是一个预测函数,接受一个输入特征和一个参数向量,然后返回一个预测:

$\hat{y}=P(x,\hat{\theta })=f(x,\hat{\theta })$(6.57)

这样就形成了一个拟合-预测循环(fit-predict cycle):

$f_m(x,D)=P(x,F(D,m))$(6.58)

对$f_m$的风险函数的K折交叉验证估计的定义为:

$R(m,D,K)\overset{\triangle}{=} \frac{1}{N}\sum^N_{k=1}\sum_{i\in D_k}L(y_i, P(x_i,F(D_{-k},m))) $(6.59)

然后就可以对每一份数据都调用运行一次拟合算法.设$f_m^k(x)=P(x,F(D_{-k},m))$是我们要对出去验证集k之外所有几何训练得到的函数.然后就可以把交叉验证估计改写成下面的形式:

$R(m,D,K)=\frac{1}{N}{\sum }_{k=1}^N{\sum }_{i\in D_k}L(y_i,f_m^{-i}(x_i))=\frac{1}{N}{\sum }_{i=1}^{N}L(y_i,f_m^{-i}(x_i))$(6.60)

上式中的$k(i)是所用的验证集所在折数(份数),而i是用作验证的数据.也就是说,我们使用一个不包含$x_i$的数据训练出的模型来预测$y_i$.

如果K=N,这个方法就成了留一交叉验证(leave one out cross validation,缩写为 LOOCV).这时候估计的风险就成了:

$R(m,D,N)=\frac{1}{N}{\sum }_{i=1}^{N}L(y_i,f_m^{-i}(x_i))$(6.61)

上式中的$f_m^{-i}(x_i)=P(x,F(D_{-i},m))$ .这需要对模型进行N次拟合,其中$f_m^{-i}$时候用到的是第i个训练样例.很幸运的是,有的模型分类和损失函数(比如线性模型和平方损失函数)可以只拟合一次,然后以解析方式每次去除掉第i个训练样本的效果.这样就叫做通用交叉验证(generalized cross validation,缩写为GCV).

6.5.3.1 样例:使用交叉验证来为岭回归选择参数$\lambda$

举个例子,比如要为一个惩罚线性回归挑选$l_2$规范项强度.可以用下面的规则:

λ ^ = arg ⁡ min ⁡ λ ∈ { λ m i n , λ m a x } R ( λ , D t r a i n , K ) \hat\lambda =\arg \min _{\lambda \in\{\lambda_{min},\lambda_{max}\}} R(\lambda,D_{train},K) λ^=argminλ∈{λmin​,λmax​}​R(λ,Dtrain​,K)(6.62)

其中的$[{\lambda }_{min},{\lambda }_{max}]$是一个有限区间,我们在这个范围内搜索$\lambda$的值,而$ R(\lambda,D_{train},K)$是使用$\lambda$之后对风险函数的K折交叉验证估计,如下所示:

$R(\lambda ,D_{train},K)=\frac{1}{D_{train}}{\sum }_{k=1}^K{\sum }_{i\in D_k}L(y_i,f_{\lambda }^k(x_i))$(6.63)

上式中的$f_{\lambda }^k(x)=x^T{\hat{w}}_{\lambda }(D_{-k})$是对除K折外数据所训练得到的预测函数,而${\hat{w}}_{\lambda }(D)=\arg {\min }_{w}NLL(w,D)+\lambda ||w|{|}_2^2$是最大后验估计(MAP).图6.6(b)所示为交叉验证估计的风险函数与KaTeX parse error: Undefined control sequence: \lamba at position 6: \log(\̲l̲a̲m̲b̲a̲)关系图像,其中的损失函数使用的是平方误差.

当进行分类的时候,通常用0-1损失函数.这时候可以在对$w_{\lambda }m$估计的经验风险上优化一个凸上界约束(convex upper bound),但我们优化了风险函数本身(对其使用交叉验证估计)来估计$\lambda$.估计$\lambda$的时候可以使用不光滑的0-1损失函数,因为这是在整个(一维)空间上使用满立法进行搜索.

当调节参数不仅一两个的时候,这个方法就不灵了.这时候可以使用经验贝叶斯,经验贝叶斯方法允许使用基于梯度的优化方法来替代蛮力查找,就可以优化大量的超参数了.这部分参考本书5.6.

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-m1q2NI32-1692517744407)(C:/Users/dell/AppData/Roaming/Typora/typora-user-images/image-20230820154709985.png)]

此处查看原书图6.6

6.5.3.2 单标准差规则(The one standard error rule)

上面的过程都是估计风险函数,但并没有给出对不确定度的衡量.在频率论中,对一个估计的不确定度的标准衡量是均值标准差,定义如下:

$se=\frac{\hat{\sigma }}{\sqrt{N}}=\sqrt{\frac{{\hat{\sigma }}^2}{N}}$(6.64)

上式中的${\hat{\sigma }}^2$是对损失函数方差的估计:

${\hat{\sigma }}^2=\frac{1}{N}{\sum }_{i=1}^N(L_i-\bar{L}{)}^2,L_i=L(y_i,f_m^{k(i)}(x_i)),\bar{L}=\frac{1}{N}{\sum }_{i=1}^N{L}_i$(6.65)

要注意这里的$\sigma$衡量的是样本空间$L_i$的内在变异性,而标准差(se)衡量的是对均值$\bar{L}$的不确定度.

对一个模型集合使用交叉验证来计算这些模型估计风险的均值和标准差.从这些有噪音估计中选择模型的一个常用的启发手段是选一个对应最简单模型的值,这个模型的风险不能超过最佳模型风险的单个标准差,这就叫单标准差规则(one standard error rule)(Hastie et al. 2001, p216).例如图6.6中,就能看到这个启发式方法并没有选择曲线上的最低点,而是选择偏右一点的点,因为那个点对应了更强规范化模型(more heavily regularized model),而经验性能本质上是一样的.

6.5.3.3 非概率无监督学习中模型选择的交叉验证(CV for model selection in non-probabilistic unsupervised learning)

如果我们进行无监督学习,就必须使用一个损失函数来衡量重建误差(reconstruction error),比如$L(x,\delta (x))=||x-\delta (x)|{|}^2$等等损失函数.这里的$\delta (x)$是某种解码编码机制(encode-decode scheme).不过我们不能使用交叉验证来确定这个$\delta$的复杂度(complexity),正如本书11.5.2所述.这是因为更复杂的模型会更少压缩数据,而降低了失真(distortion).所以要么使用概率模型,要么就用其他的启发式模型.

6.5.4 使用统计学习理论的风险上界(Upper bounding the risk using statistical learning theory)*

交叉验证的根本问题是速度太慢,因为必须对模型进行多次拟合.这就使得我们更希望计算泛化误差(generalization error)的解析近似或者上下界.这个问题是统计学习理论(statistical learning theory,缩写为SLT)的研究范围.具体来说,统计学习理论(SLT)所做的是对任意数据分布$p_{\ast }$来建立其风险函数$R(p_{\ast },h)$的边界约束,$h\in H$是假设,$R_{emp}(D,h)$是经验风险(empirical risk),取样规模$N=|D|$,H就是假设空间规模.

首先考虑假设空间有限的情况,也就是有固定的$(H)=|H|$.也就是说,要从一个有限的列表中选择一个模型或者假设,而不是优化实数值参数.这样就可以证明有下面的结论了.

定理 6.5.1

对于任意数据分布$p_{\ast }$,以及任意从$p_{\ast }$中取样得到的规模为N的数据集D,则我们估计的误差率(errir rate)超过错误率(wrong)$ϵ$的概率的上界为(这也就是最坏的情况):

$P({\max }_{h\in H}|R_{emp}(D,h)-R(p_{\ast },h)|>ϵ)\le 2dim(H)e^{-2N{ϵ}^2}$(6.66)

证明. 要证明这个,需要两个有用的结论.首先是霍夫丁不等式(Hoeffding’s inequality),说的是如果有N个伯努利分布,$X_1,...,X_N\sim Ber(\theta )$,对于任意的$ϵ>0$,则有:

$P(|\bar{x}-\theta |>ϵ)\le 2e^{-2N{ϵ}^2}$(6.67)

上式中的$\bar{x}=\frac{1}{N}{\sum }_{i=1}^N{x}_i$.
第二个结论是联合约束(union bound),说得是如果$A_1,...,A_d$是一系列事件集合,那么有$P(U_{i=1}^d{A}_i)\le {\sum }_{i=1}^{d}P(A_i)$.

最后为了表述简洁,设$R(h)=R(h,p_{\ast })$表示真实风险函数(true risk),而${\hat{R}}_N(h)=R_{emp}(D,h)$是经验风险函数(empirical risk).

利用上面的结论,就得到了:

$$\begin{array}{rlr}P(\underset{h\in H}{\max }|{\hat{R}}_N(h)-R(h)|>ϵ)& =P(U_{h\in H}|{\hat{R}}_N(h)-R(h)|>ϵ)& \text{(6.68)}\\ & \le \sum _{h\in H}P(|{\hat{R}}_N(h)-R(h)|>ϵ)& \text{(6.69)}\\ & \le \sum _{h\in H}2e^{-2N{ϵ}^2}=2dim(H)e^{-2N{ϵ}^2}& \text{(6.70)}\end{array}$$

这个上界的约束条件标明训练误差的优化会随着$dim(H)$提高而提高,但又随着$N=|D|$而降低,正如我们所料.

如果假设空间H是无穷的,比如说是实数值参数了,那就不能使用$dim(H)=|H|$了.这时候要使用VC维度(Vapnik-Chervonenkis ,缩写为VC).具体细节参考(Vapnik 1998).

回到理论上来看,统计学习背后的关键思想其实很简单.假如要找一个低经验风险的模型.如果假设空间H相对于数据规模来说非常大,那么我们很幸运,得到的数据就碰巧能用我们选中的函数建模.不过这并不意味着这样的一个函数就有很低的泛化误差.但如果假设类别的规模特别有限,或者训练及规模超级大,那我们可能就不能那么幸运了,所以具有低经验风险才能证明真正有低风险.

要注意对训练误差的优化并不一定就随着模型复杂度的提高而改善,但会随着搜索的不同模型数目而增加.

统计学习理论相比交叉验证来说,有一个优势,就是风险函数的上界约束比交叉验证算起来更快.缺点就是很多有用模型都很难算出VC维度,而且上界通常也可能很松散(参考 Kaariainen and Langford 2005).

可以通过加入学习程序的复杂度计算来扩展统计学习理论.这个领域就叫做计算学习理论(computationa learning theory,缩写为COLT).大多数这类研究关注的都是当h是二分类,而损失函数为0-1损失的情况.如果观察到了一个低经验风险的情况,那么架设样本空间就适当地小,然后就可以说这个估计函数是可能近似正确的(probably approximately correct,缩写为PAC).如果使用多项式规模复杂度的算法能够找到一个可能近似正确(PAC)的函数,就说这个假设空间是有效PAC可学习的(efficiently PAC-learnable).更多内容参考(Kearns and Vazirani 1994).

6.5.5 代理损失函数(Surrogate loss functions)

在经验误差最小化(ERM)/规范误差最小化(RRM)框架中最小化损失函数并不总是很简单.例如可能要优化曲线所覆盖的面积(AUC)或者F1分数.或者更简单的情况,在分类里面需要最小化0-1损失函数.可很不幸的是0-1风险函数是非光滑的,所以很难去优化.替代方法就是用最大似然估计替代,因为对数似然函数是个光滑凸函数,上界就是0-1风险函数,下面就来将这个.

考虑二项逻辑回归,设 y i ∈ { − 1 , 1 } y_i\in \{-1,1\} yi​∈{−1,1}.然后设我们的决策函数计算量对数比值:

$f(x_i)=\log \frac{p(y=1|x_i,w)}{p(y=-1|x_i,w)}=w^T{x}_i={\eta }_i$(6.71)

然后对应的输出标签上的概率分布就是:

$p(y_i|x_i,w)=sigm(y_i,{\eta }_i)$(6.72)

接下来定义对数损失函数(log-loss)为:

$L_{nll}(y,\eta )=-\log p(y|x,w)=\log (1+e^{-u\eta })$(6.73)

此处查看原书图6.7

很明显,最小化平均对数损失函数就等价于最大化似然函数.

接下来设要计算最大概率标签,也就是等价于使用如果${\eta }_i<0$,则$\hat{y}=-1$,如果$\eta \ge 0$,则$\hat{y}=+1$.这样函数的0-1损失函数就是:

$L_{01}(y,\eta )=I(y\ne \hat{y})=I(y\eta <0)$(6.74)

图6.7所示的就是这两个不同的损失函数,很明显负对数似然函数(NLL)就是在0-1损失函数的上界上.
对数损失是代理损失函数(surrogate loss function)的一个例子.另外一个是铰链损失函数(hinge loss):

$L_{hinge}(y,\eta )=\max (0,1-y\eta )$(6.75)

如图6.7所示,这个函数看着像是门的铰链,因此得名.这个损失函数一种流行的分类方法的基础,这种流行方法就是支持向量机(support vector machine,缩写为SVM),在本书14.5会讲到.

代理损失函数通常是选凸上界的函数,因为凸函数容易最小化.更多信息参考(Bartlett et al. 2006).

6.6 频率论统计学的缺陷(Pathologies of frequentist statistics)*

说服一个聪明人去接受频率论统计学在实践中的应用是很困难的,但如果用似然函数和贝叶斯定理之类的方法来讲就容易接受了.— George Box, 1962.

频率论统计学有各种各样怪异又难缠的缺陷.本节部分就是讲一个例子来简单展示一下,更多细节参考(Lindley 1972; Lindley and Phillips 1976; Lindley 1982; Berger 1985; Jaynes 2003; Minka 1999).

6.6.1 置信区间的反直觉行为

置信区间(confidence interval)就是一个区间,是从估计器的抽样分布中推导出来的(在贝叶斯理论统计学中,置信区间是从一个参数的后验中推导出来的,参考本书5.2.2).具体来说,对于某个参数$\theta$的频率论的置信区间定义如下(相当反直觉不自然反人类!):
$C_{\alpha }^{\prime }(\theta )=(l,u):P(l(\tilde{D})\le \theta \le u(\tilde{D})|\tilde{D}\sim \theta )=1-\alpha$(6.76)

也就是说,如果我们从$\theta$中取样假设的未来数据$\tilde{D}$,然后就有$(l(\tilde{D}),u(\tilde{D}))$就是参数$\theta$在这个$1-\alpha$比例内所在的置信区间.

在贝叶斯统计学里面,我们的条件是建立在已知上的,也就是已经观测到的数据D,而在未知参数$\theta$上取平均,.在频率论统计里,正好相反,我们将条件建立在未知上,即真实参数值$\theta$,取平均却是在假设的未来数据集$\tilde{D}$上.

这样对置信区间的定义是很违背直觉的,会带来很多怪异结果.比如下面这个例子来自(Berger 1985, p11).设要从$D=(x_1,x_2)$中取两个区间:

$p(x|\theta )=\{\begin{array}{ll}0.5& \text{ if }x=\theta \\ 0.5& \text{ if }x=\theta +1\\ 0& \text{ otherwise}\end{array}$(6.77)

如果$\theta =39$,那就期待下面每个区间的出现概率都是0.25:

$(39,39),(39,40),(40,39),(40,40)$(6.78)

设$m=\min (x_1,x_2)$,然后定义下面的置信区间:

$[l(D),u(D)]=[m,m]$(6.79)

从上面的抽样就得到了:

$[39,39],[39,39],[39,39],[40,40]$(6.80)

因此等式6.79是一个75%的置信区间(CI),因为39有75%的概率被包含在这些区间中.可是如果$D=(39,40)$,$p(\theta =39|D)=1.0$,就知道$\theta$ 必须是39了,虽然事实上对此只有75%的置信度.

再举个例子.设要估计一个伯努利分布的参数$\theta$.设其取样均值为:$\bar{x}=\frac{1}{N}{\sum }_{i=1}^N{x}_i$.最大似然估计(MLE)就是$\hat{\theta }=\bar{x}$.对一个伯努利分布参数的近似95%置信区间就是$\bar{x}\pm 1.96\sqrt{\bar{x}(1-\bar{x})/N}$(这个也叫瓦尔德区间,Wald interval,是来自对二项分布的高斯估计,可以和等式3.27相对照.)然后有一个单次试验,其中$N=1,x_1=0$.这样最大似然估计(MLE)就是0,过拟合了,可以参考本书3.3.4.1.可是这时候的95%置信区间也还是(0,0),看着更差.可能是因为之前用了高斯分布估计了真实样本分布,或者可能是因为样本规模太小,又或者就是真实参数太极端.不过实际上即便规模很大的N或者不极端的参数下,瓦尔德区间(Wald interval)效果也不好(Brown et al. 2001).

6.6.2 P值(p-values)是祸害

假设我们想要决定是否接受某个基准模型(baseline model,称其为零假设(null hypothesis).需要先定义某个决策规则.在频率统计学中,标准做法是计算一个叫做P值(p-values)的量,定义是观测到跟实际观测规模相当或更大的某个测试统计(test statistic)$f(D)$(比如卡方分布统计等)的概率(在零假设条件下):

$pvalue(D)\stackrel{△}{=}P(f(\tilde{D})\ge f(D)|\tilde{D}\sim H_0)$(6.81)

这个量依赖于取样分布的尾部面积概率(tail area probability);下面是一个例子.

给定一个p值,我们定义如下的决策规则:当且仅当p值小于某个阈值,比如$\alpha =0.05$的时候我们才拒绝零假设.如果拒绝了,就说观测测试统计和预期测试统计之间的差异在$\alpha$程度上统计学显著(statistically significant).这个方法也叫做零假设显著性检验(null hypothesis significance testing,缩写为NHST).

这个过程保证了我们期望的第一类误差率(假阳性)最大为$\alpha$.有时候就有人将这解释为频率论假设检验很保守,因为很不容易意外拒绝零假设.但实际上正好相反:因为这个方法值考虑了对零假设的拒绝,所以不论样本规模多大,也从来不收集对零假设有利的证据.因此,P值总是倾向于夸大反对零假设的证据,容易引发误判(very “trigger happy”).

一般来说,P值和我们真正关心的量之间差别巨大,我们真正关心的是给定数据后零假设的后验概率$p(H_0|D)$.具体来说,Sellke 等(2001)一篇文章中表明即便P值小到0.05,$H_0$的后验概率还是可能高达至少30%甚至更高.所以频率论者常说有充分证据表明了一个不能用零假设解释的效应,而贝叶斯主义者就常常会有更保守的判断.比如,P值曾被用来证明超感官知觉(extra-sensory perception,缩写为ESP)是真实的(Wagenmakers et al. 2011),虽然大家明知道那就是扯.因此某些医学杂志早就禁止使用P值了((Matthews 1998)).

P值的另外一个问题是其计算依赖于停止收集数据的决策,即便这些决策对你已经观测到的数据并无影响.比如加入我抛了硬币n=12次,然后观测到了s=9次人头朝上,f=3次背面朝上,则n=s+f.这时候n是固定的,但s和f都是随机的,所以相关的抽样分布就是二项分布:

$Bin(s|n,\theta )=\left(\begin{array}{c}n\\ s\end{array}\right){\theta }^s(1-\theta {)}^{n-s}$(6.82)

设零假设就是硬币没有作弊,即$\theta =0.5$,这个$\theta$是人头朝上的概率.这样使用检验统计$t(s)=s$得到的单边p值(one-sided p-value)就是:

$p_1=P(S\ge 9|H_0)={\sum }_{s=9}^{12}Bin(s|12,0.5)={\sum }_{s=9}^{12}\left(\begin{array}{c}12\\ s\end{array}\right)0.5^{12}=0.073$(6.83)

双边P值(two-sided p-value)就是:

$p_2={\sum }_{s=9}^{12}Bin(s|12,0.5)+{\sum }_{s=0}^{3}Bin(s|12,0.5)=0.073+0.073=0.146$(6.84)

这两种情况中,P之都比神奇的5%阈值要大很多,所以频率论就不会拒绝零假设了.

然后设想我告诉你我一直扔硬币,直到我观测到了$f=3$次人头朝下为止.这时候f是固定的,而n和s是随机的.所以这时候概率模型就成了负二项分布(negative binomial distribution,):

$NegBinom(s|f,\theta )=\left(\begin{array}{c}s+f-1\\ f-1\end{array}\right){\theta }^s(1-\theta {)}^f$(6.85)
上式中的f=n-s.

要注意这个分布中依赖于$\theta$的项目和等式6.82与6.85中的是一样的,所以在$\theta$上的后验在两种情况下也都是一样的.不过对同样数据的两种解释给出了不同的P值.具体来说就是在负二项分布情况下的p值是:

$p_3=P(S\ge 9|H_0)={\sum }_{s=9}^{\infty }\left(\begin{array}{c}s+3-1\\ 3-1\end{array}\right)(1/2{)}^s(1/2{)}^3=0.0327$(6.86)

这P值是3%,这样好像很明显硬币被做了手脚了!当然这很荒诞了,因为数据都是一样的,明显对硬币的推测也应该一样才对.不论如何也都是随机选择的实验协议.最重要的应该是试验结果,而不是对使用哪种试验方式的人为判断.

虽然这看上去有点像数学上的弯弯绕,但实际应用中也是有很大影响的.比如由于停止规则(stopping rule)影响到P值的计算,这就意味着频率论这往往倾向于推迟终结试验,甚至即便已经有明显结论了也是如此,至少这会严重影响他们的统计分析.如果试验成本很高而且对人有害,使用频率论和P值就明显是祸害.所以毫不意外,美国食品药品管理局(FDA)在对新药的测试中,都明确支持了贝叶斯方法了,因为贝叶斯方法不会受停止规则的影响.

6.6.3 似然性原则

频率论方法出现很多问题的根源所在就是违背了似然性原则(likelihood principle),这个原则是说推测应该建立在观测数据的似然率上,而不是建立在没观测到的假设未来数据上.贝叶斯方法明显满足这个原则,所以也就不会有频率论所遇到的那么多问题了.

Birnbaum 1962年提出了一个支持似然性原则的有力证据,其文章表明这个原则自觉遵循了两个更简单的原则.第一个就是充分原则(sufficiency principle),说的是一个充分统计应该包含了和未知参数相关的所有信息(定义即证明).第二个是弱条件原则(weak conditionality),说的是推论应该基于已经发生的事件,而不是可能发生的时间.要推导出这个,可以考虑Berger 1985年的一个例子.加入我们要分析一种物质,可以把它发到纽约或者加利福尼亚的实验室.这两个实验室都挺好,所以就用公平硬币假设.如果人头朝上,就选加州哪个实验室.当测试这个物质的结果回来的时候,会不会考虑硬币本来也可能背面朝上所以本来也可能应该送到纽约的实验室呢?大多数人会说因为硬币背面朝上没发生所以纽约的实验室与此无关.这就是一个弱条件的例子.给定了这个原则之后,就能发现所有推论都应该基于被观测到的现象上,而这对于标准频率论过程来说是恒定的.关于似然性原则的更多细节参考Berger and Wolpert 1988.

6.6.4 为啥大家不都选贝叶斯?

上文已经表明,频率论统计有种种缺陷,而贝叶斯方法却没有,那有人可能就会问:"为啥大家不都选贝叶斯?"1986年有一个频率论统计学家Bradley Efron还就以此为标题写过一篇文章.他这篇文章不长,但是很值得读一读.下面是他文章的开头部分:

标题的这个问题被提出至少两次了.第一次是拉普拉斯(Laplace)曾经问过这个问题,他曾经是一个贝叶斯主义者,完全赞同贝叶斯公式来推断问题,十九世纪的大多数科学家也纷纷认同.这其中包含高斯(Gauss),而高斯的很多统计学方面的研究都是以频率论形式阐述的.
第二次出现这个问题是关于贝叶斯合理性的争论.以Savage和 de Finetti为首的现代统计学家,对选中贝叶斯方法给出了很多高级的有力的理论证据.这个工作的副产物是频率论者眼中的术语不一致冲突.
尽管如此,并不是所有人都是贝叶斯主义者.在当前(1986年)统计学终于开始广泛用于科研报道中了,而实际上二十世纪的统计学主要还是非贝叶斯的.不过Lindley(1975)预测这一情况会在21世纪发生变化.

时间会检验Lindley说的是不是对的…

练习略

也可能背面朝上所以本来也可能应该送到纽约的实验室呢?大多数人会说因为硬币背面朝上没发生所以纽约的实验室与此无关.这就是一个弱条件的例子.给定了这个原则之后,就能发现所有推论都应该基于被观测到的现象上,而这对于标准频率论过程来说是恒定的.关于似然性原则的更多细节参考Berger and Wolpert 1988.

6.6.4 为啥大家不都选贝叶斯?

上文已经表明,频率论统计有种种缺陷,而贝叶斯方法却没有,那有人可能就会问:"为啥大家不都选贝叶斯?"1986年有一个频率论统计学家Bradley Efron还就以此为标题写过一篇文章.他这篇文章不长,但是很值得读一读.下面是他文章的开头部分:

标题的这个问题被提出至少两次了.第一次是拉普拉斯(Laplace)曾经问过这个问题,他曾经是一个贝叶斯主义者,完全赞同贝叶斯公式来推断问题,十九世纪的大多数科学家也纷纷认同.这其中包含高斯(Gauss),而高斯的很多统计学方面的研究都是以频率论形式阐述的.
第二次出现这个问题是关于贝叶斯合理性的争论.以Savage和 de Finetti为首的现代统计学家,对选中贝叶斯方法给出了很多高级的有力的理论证据.这个工作的副产物是频率论者眼中的术语不一致冲突.
尽管如此,并不是所有人都是贝叶斯主义者.在当前(1986年)统计学终于开始广泛用于科研报道中了,而实际上二十世纪的统计学主要还是非贝叶斯的.不过Lindley(1975)预测这一情况会在21世纪发生变化.

时间会检验Lindley说的是不是对的…

练习略