LDA降维

还记得在PCA中是怎样做的吗？简单来说，是将数据映射到方差比较大的方向上，最后用数学公式推导出矩阵的前TopN的特征向量，这里的方差可以理解为数据内部的离散程度。而LDA不同于PCA的是它是一种有监督的降维方法。下面举一个小例子来直观的说明PCA和LDA的不同降维方法。

例子

如下图所示为两类数据集:

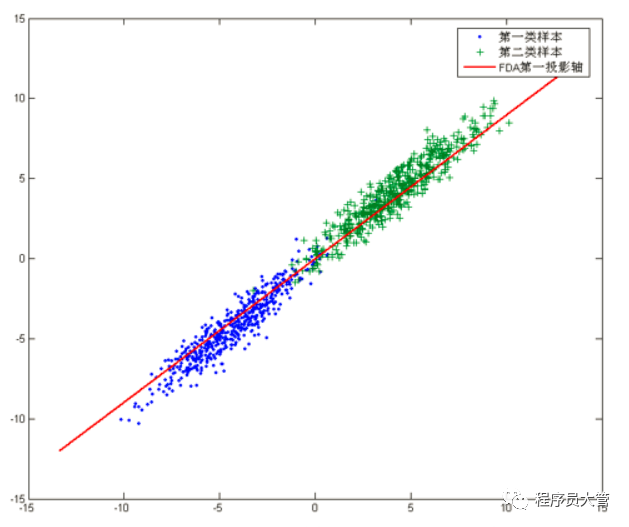
PCA是将数据投影到方差最大的几个相互正交的方向上，以期待保留最多的样本信息。样本的方差越大表示样本的多样性越好。x轴和y轴都不是最理想的投影，故上图中PCA会将数据投影在红色的轴上。

如下图所示数据集:

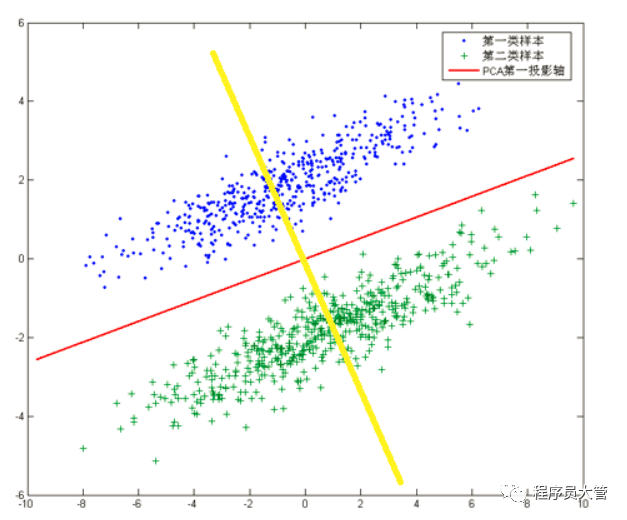
若根据PCA进行降维，将会把数据映射到红色直线上，这样做投影确实方差最大，但是这样做投影之后两类数据样本将混合在一起，将不再线性可分，甚至是不可分的。上面的这个数据集如果使用LDA降维，找出的投影方向就是黄色直线所在的方向，这样的方法在降维之后，可以很大程度上保证了数据的线性可分的。

LDA降维

从上述例子中可以看到，LDA可以用来对数据分类进行处理。为了说明白LDA的来龙去脉，还是以最简单的二分类问题为例。

假设有C1和C2两个样本数据集，其均值分别为:

$\begin{array}{rl}{\mu }_1& =\frac{1}{N_1}\sum _{x\in C_1}x\\ & \\ {\mu }_2& =\frac{1}{N_2}\sum _{x\in C_2}x\end{array}$

投影之后的类间距离为:
$$\mathrm{D}(C_1,C_2)=||\widetilde{{\mu }_1}-\widetilde{{\mu }_2}|{|}_2^2$$

其中成和或为两个类中心在方向上的投影向量

$$\begin{array}{l}\widetilde{{\mu }_1}={\omega }^T{\mu }_1\\ \widetilde{{\mu }_2}={\omega }^T{\mu }_2\end{array}$$

将上述两式合并，求最大间距可以表示为:

$\{\begin{array}{cc}{\max }_{\omega }||{\omega }^T({\mu }_1-{\mu }_2)|{|}_2^2& \\ & \\ s.t.& {\omega }^T\omega =1\end{array}$

当 ω 方向与(μ1-μ2)一致的时候，该距离达到最大值。从所举的例子图中也能看出，我LDA的期望是使得两个类间的距离最大，类内的距离最小。

由于不同的类别是在同一个数据集中，所以类内距离也可以定义为不同类的方差之和。故可以定义LDA的目标函数为:

${\max }_{\omega }J(\omega )=\frac{{\Vert {\omega }^{\mathrm{T}}\left({\mu }_1-{\mu }_2\right)\Vert }_2^2}{D_1+D_{\text{’}2}}$

其中D1和D2分别为两个类的类内距离，分别为:

$\begin{array}{c}{D}_1=\sum _{x\in C_1}{\omega }^T(x-{\mu }_1)(x-{\mu }_1{)}^T\omega \\ D_2=\sum _{x\in C_2}{\omega }^T(x-{\mu }_2)(x-{\mu }_2{)}^T\omega \end{array}$

将D1和D2分别代入，J(ω)可以表示为:

$J(\omega )=\frac{{\omega }^{\mathrm{T}}\left({\mu }_1-{\mu }_2\right)({\mu }_1-{\mu }_2{)}^{\mathrm{T}}\mathbf{\omega }}{{\sum }_{x\in C_l}{\mathbf{\omega }}^{\mathrm{T}}\left(x-{\mu }_i\right)(x-\mathbf{\mu }{)}^{\mathrm{T}}\mathbf{\varrho }}$

为了简化上述公式，这里定义类间距离散度SB和类内距离散度SW分别为:

$\begin{array}{rl}{S}_B& =({\mu }_1-{\mu }_2)({\mu }_1-{\mu }_2{)}^T\\ S_w& =\sum _{x\in C_i}(x-{\mu }_i)(x-{\mu }_i{)}^T\end{array}$

故可以将式子简化为:

$J(\omega )=\frac{{\omega }^{\mathrm{T}}{S}_B\omega }{{\omega }^{\mathrm{T}}{S}_w\omega }$

下面使用烂大街而有效的方法最大化J(ω)，对ω求偏导，并令其为0,得到：

$({\mathbf{\omega }}^{\mathrm{T}}{\mathbf{S}}_w\mathbf{\omega }){\mathbf{S}}_B\mathbf{\omega }=({\mathbf{\omega }}^{\mathrm{T}}{\mathbf{S}}_B\mathbf{\omega }){\mathbf{S}}_W\mathbf{\omega }$

下面对公式稍作变化，就可以发现一个令人惊讶的结果:

$S_B\omega=\frac{(\omega^{TS_w\omega)}{(\omega}TS_B\omega)}S_w\omega $

将Sw乘到左边:

$\begin{array}{rl}{S}_w^{-1}{S}_B\omega & =\frac{({\omega }^T{S}_w\omega )}{({\omega }^T{S}_B\omega )}\omega \\ & \\ S_w^{-1}{S}_B\omega & =\lambda \omega \end{array}$

我们居然把目标函数变成了求矩阵的特征值，而投影的方向就是这个特征值对应的特征向量。故对于二分类问题在不考虑投影长度的情况下，我们只要求得样本的均值和类内方差就可以计算出投影方向。

回顾PCA的过程，是不是和LDA很相似呢，但是其原理却不一样，对于无监督学习使用PCA，有监督学习使用LDA。
本的均值和类内方差就可以计算出投影方向。

回顾PCA的过程，是不是和LDA很相似呢，但是其原理却不一样，对于无监督学习使用PCA，有监督学习使用LDA。