目录
算法思想:
- 创建一个path线性表,记录源点到各点的最短路径。path[i]记录的是源点到顶点i的最短路径中,到达i的上一个顶点。若为-1,则不存在路径。
- 创建一个dist线性表,记录源点到各点的当前最短距离。dist[i]记录的是源点到顶点i的最短距离,若不存在则记为INT_MAX。
- 创建一个vist线性表,记录各个顶点是否已经在最短路径里,并将所有顶点的记录初始化为false。
- 在dist里挑选一个最短距离且目前还不在最短路径里的顶点,被挑选完的顶点在vist里的记录改为true。
- 在每次挑选完最短距离后,将本次的最短距离顶点作为距离刷新点,刷新源点到各个顶点的距离。
- 重复上述操作,直到所有顶点的path记录均被操作过(可能会修改,也可能保持-1)
具体代码实现:
#include<iostream>
#include<vector>
#include<queue>
#include<stack>
using namespace std;
class dirctedEdge {
public:
dirctedEdge(int v, int w, double weight) {
this->v = v;
this->w = w;
this->weight = weight;
}
int getWeight() {
return this->weight;
}
int getStartPoint(int w) {
if (w == this->w)
return this->v;
else
return this->w;
}
int getEndPoint(int v) {
if (v == this->v)
return this->w;
else
return this->v;
}
private:
int v;//边的起点
int w;//边的终点
double weight;//边的权重
};
class cmp {
public:
cmp() {};
bool operator () (int &a, int &b) {
return a > b;
}
};
class Graph {
public:
Graph(int v) {
this->V = v;
this->E = 0;
for (int i = 0; i < v; i++) {
vector<dirctedEdge> e;
this->vde.push_back(e);
}
}
void addEdge(int v, int w, double weight) {
dirctedEdge de(v, w, weight);
this->vde[v].push_back(de);
this->E += 1;
}
int getMinPoint(vector<int>& dist, vector<bool>& vist) {
int i = 0;
int minW;
int min = INT_MAX;
while (i < this->V){
if (!vist[i]) {
if (min > dist[i]) {
min = dist[i];
minW = i;
}
}
i++;
}
return minW;
}
vector<int> Dijkstra(int v, int w) {
//构建最短路径树path:存储源点v到图中其他点的最短路径
//path[i]记录的是源点到顶点i的最短路径中,到达i的上一个顶点。若为-1,则不存在路径
vector<int> path(this->V, -1);//默认初始源点跟其他顶点都不存在路径
path[v] = v;//源点到本身的最短路径就是本身
//创建一个容器,存储源点到其他各点的距离,初始为无穷大,默认两点间不存在路径
vector<int> dist(this->V, INT_MAX);
dist[v] = 0;//源点到本身的路径权值为0
//创建一个容器,记录各点的访问状态
vector<bool> vist(this->V, false);
vist[v] = true;
for (auto e : this->vde[v]) {
dist[e.getEndPoint(v)] = e.getWeight();//初始化源点能直接到达的顶点路径权值
path[e.getEndPoint(v)] = v;//到达该点的最短路径权值目前就是源点
}
int mw;
do {
mw = getMinPoint(dist, vist);
vist[mw] = true;
//把本次的最短点作为中转点,刷新源点v到其他各点的距离
for (auto e : this->vde[mw]) {
if (dist[e.getEndPoint(mw)] == -1 || dist[e.getEndPoint(mw)] > dist[mw] + e.getWeight()) {
dist[e.getEndPoint(mw)] = dist[mw] + e.getWeight();
path[e.getEndPoint(mw)] = mw;//修改源点到该点的最短路径树
}
}
} while (mw != w);
return path;
}
void printPath(vector<int>& path, int v, int w) {
stack<int> spath;
if (path[w] == -1) {
cout << "源点" << v << "跟点" << w << "之间不存在路径!" << endl;
return;
}
while (w != v) {
spath.push(w);
w = path[w];
}spath.push(v);
while (!spath.empty()) {
cout << spath.top();
if (spath.size() != 1) {
cout << "->";
}
spath.pop();
}cout << endl;
}
private:
int V;//图的顶点数
int E;//图的边数
vector<vector<dirctedEdge>> vde;//图中每个顶点的边
};
int main()
{
Graph g(7);
g.addEdge(0, 1, 4);
g.addEdge(0, 2, 6);
g.addEdge(0, 3, 6);
g.addEdge(1, 2, 1);
g.addEdge(3, 2, 2);
g.addEdge(3, 5, 5);
g.addEdge(2, 5, 4);
g.addEdge(1, 4, 7);
g.addEdge(2, 4, 6);
g.addEdge(5, 4, 1);
g.addEdge(5, 6, 8);
g.addEdge(4, 6, 6);
int v, w;
cout << "请输入您想查询的源点和终点:";
cin >> v >> w;
vector<int> path = g.Dijkstra(v, w);
g.printPath(path, v, w);
system("pause");
return 0;
}构建的图及运行结果:
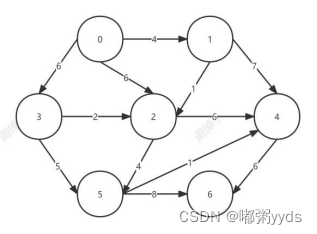
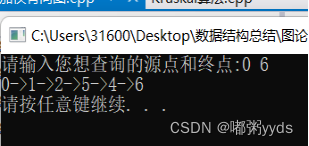





















 570
570











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








