目录
1.引子
通常,对图像进行多次卷积运算后,特征图的尺寸会不断缩小。不论是语义分割、检测还是三维重建等模型,都需要将提取到的高层特征进行放大,此时就需要对feature map进行上采样(由特征点热图得到预测图)。
转置卷积 在语义分割或者对抗神经网络(GAN)中比较常见,其主要作用就是做上采样(UpSampling)。经常被称反卷积,逆卷积。但在主流的深度学习框架之中,如Tensorflow,Pytorch,Kreas中的函数名都是conv_transpose,都是表示转置卷积。因为本质上说,转置卷积并不是卷积操作的逆运算。
所以我们一定要记住其正确的名称--转置卷积。
2.普通卷积
首先来回顾下普通的卷积操作吧。
普通的卷积操作可以说是很简单,就是卷积核大小的窗口在原始输入图像的一步步挪动,通过加权计算得到结果。
下图以stride=1,padding=1,kernel_size=3为例,假设输入特征图大小是4x4的(假设输入输出都是单通道),通过卷积后得到的特征图大小为2x2。一般使用卷积的情况中,要么特征图变小(stride > 1),要么保持不变(stride = 1),
当然也可以通过四周padding让特征图变大但没有意义。下图对padding进行扩充就可以让输入输出特征图大小相同。
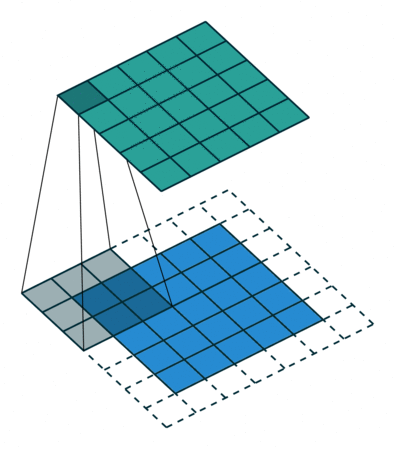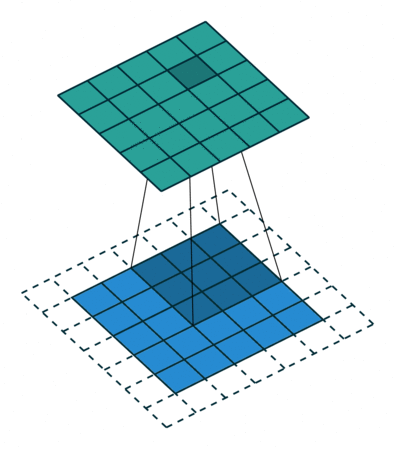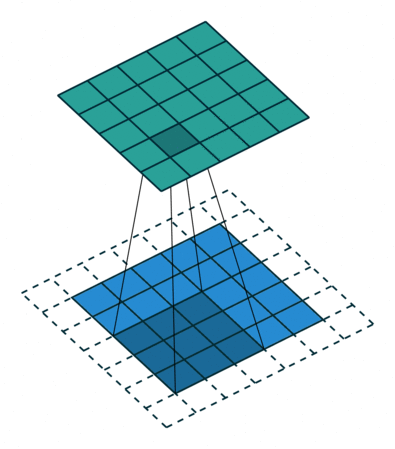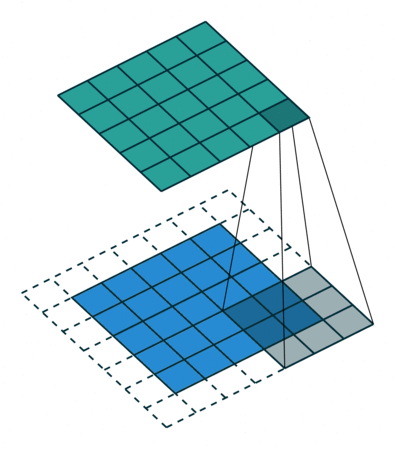
但是实际在计算机中计算的时候,并不是像这样一个位置一个位置的进行滑动计算,因为这样的效率太低了。计算机会将卷积核转换成等效的矩阵,将输入转换为向量。通过输入向量和卷积核矩阵的相乘获得输出向量。输出的向量经过整形便可得到我们的二维输出特征。
具体转化过程可以示例如下。
对于一个输入大小为的图像,卷积核大小为
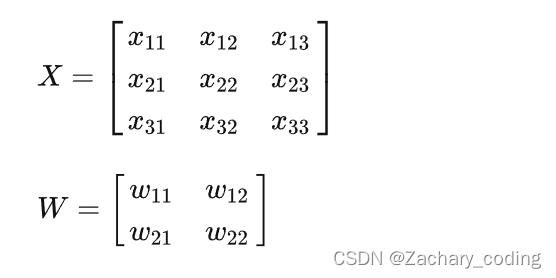
计算机在操作时会将卷积核表示为稀疏矩阵。
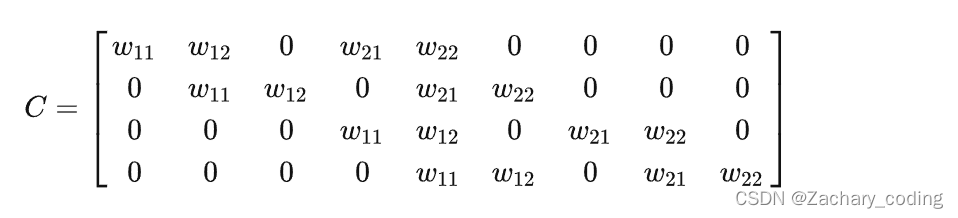
那具体是如何表示为稀疏矩阵的呢,可以想象在输入矩阵中每次移动的卷积核大小的小窗口,将其周围都填充为0后,再将其转变为一个行向量。
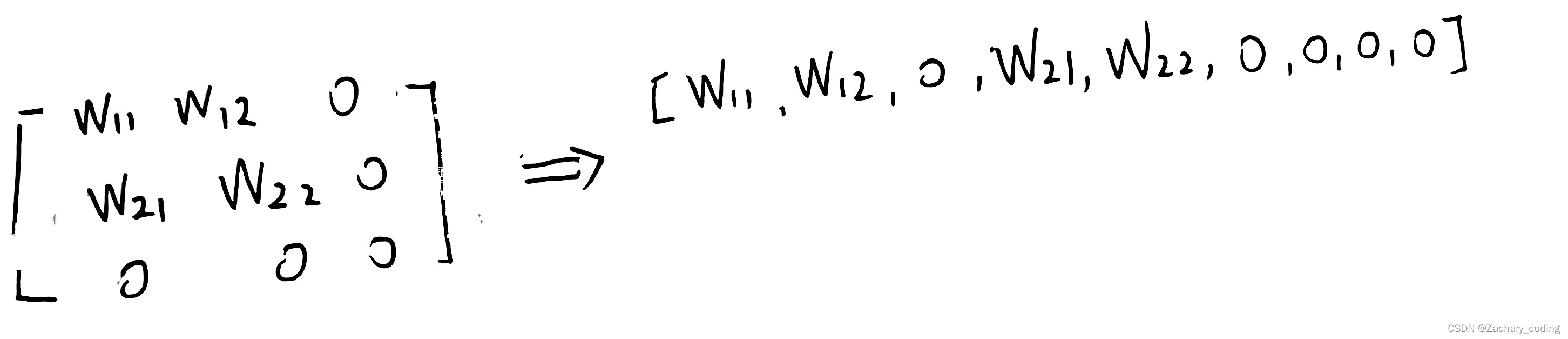
将所有的窗口进行操作后就可以变成稀疏矩阵。
将输入 展开为列向量:
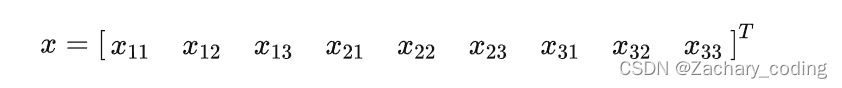
则卷积操作可以表示为
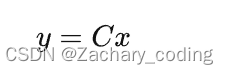
3.转置卷积
3.1与普通卷积的不同
以认为标准卷积操作实际上就是建立了一个 多对一的映射关系。
转置卷积而言,我们实际上是想建立一个逆向操作,即 一对多的映射关系。这样才可以实现图像的放大,从而完成上采样。那这里你可能要问了,不是说不是逆操作吗,你是不是骗人?
我当然没有,因为从信息论的角度看,卷积是不可逆的.所以这里说的并不是从output矩阵和kernel矩阵计算出原始的input矩阵.而是计算出一个保持了位置性关系的矩阵.简单来说,对于同一个卷积核,经过转置卷积操作之后并不能恢复到原始的数值,保留的只有原始的形状。
3.2转置卷积具体运算操作
3.2.1stride=1的情况:
如上面普通卷积的运算过程所示。
所谓转置卷积就是将中的输入输出互换:

即由原来的的输入
,经过转置卷积可以得到
的列向量
,此时的
数值上已经和原来不同,只是在形状上一致。ze
考虑上文的二维卷积的矩阵 :
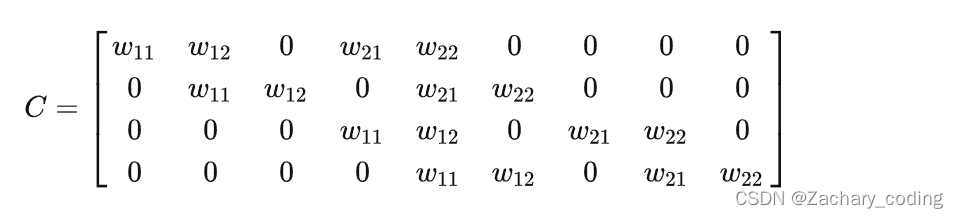
令转置卷积输入为
,对应向量
(注意这里的输入y与普通卷积的输出y没有关系,这里是转置卷积的独立操作,也就是通过同样的输入和卷积核来得到输出形状变大的结果)
则转置卷积结果为
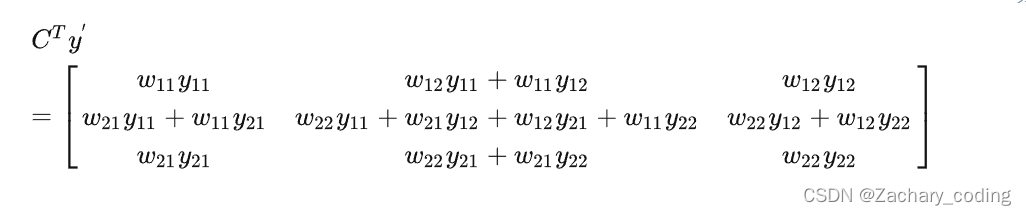
这等价于输入padding = 1的输入

和水平和竖直方向镜像翻转的卷积核
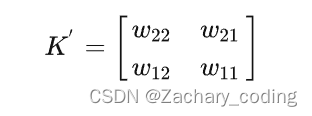
之间进行普通卷积的结果。
可以用一个动图更形象的表示,(此处动图与上面所举例子不同,但可以做个参考)
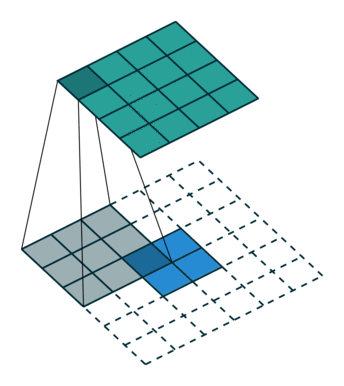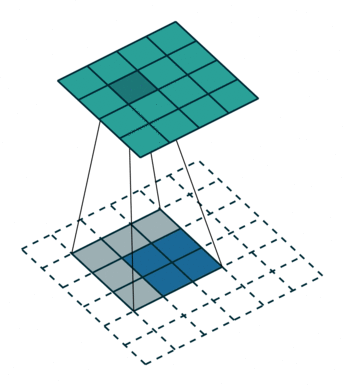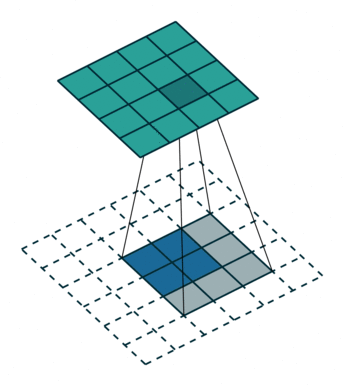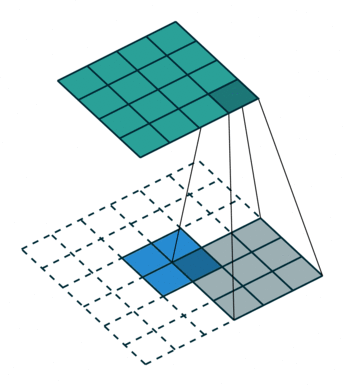
从中可以看出直接卷积我们是用一个“小窗户”去看一个“大世界”,而转置卷积是用一个“大窗户”的一部分去看“小世界”。
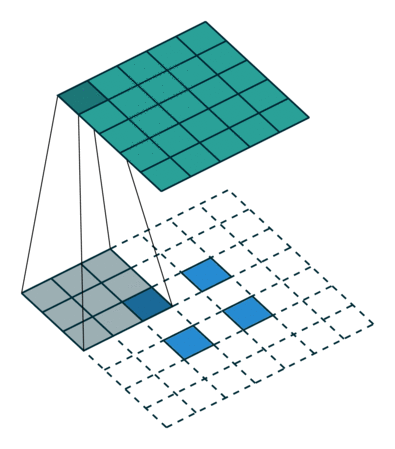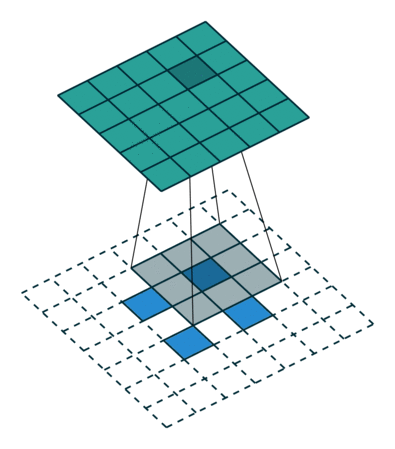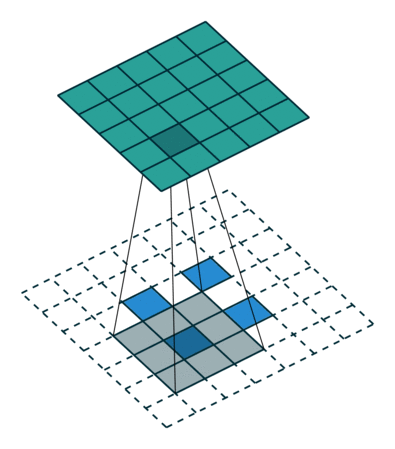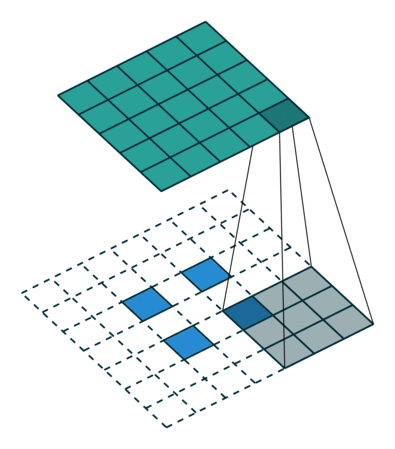
3.2.1stride>1的情况:

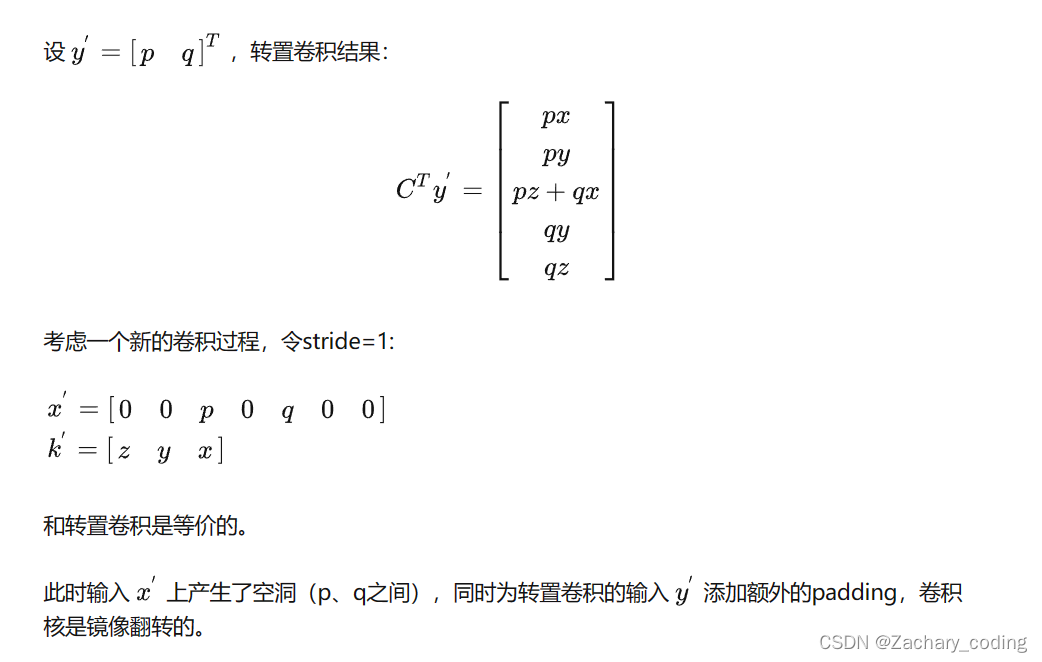
对于输入为的图像,卷积核大小为
,stride-2,padding=0,普通卷积卷积后输出大小为
的矩阵。
设卷积核为
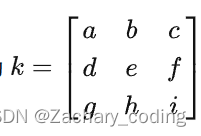
设输入则转置卷积结果为
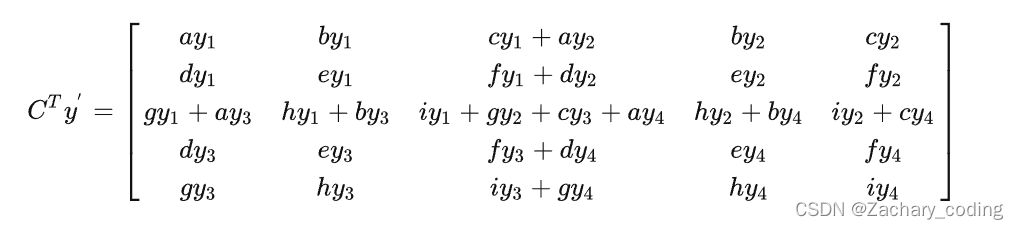
同样等价于输入添加空洞,额外padding,卷积核水平竖直翻转的普通卷积:

对应的图像如下
3.3转置卷积公式计算归纳
设步长stride为s,填充padding=1,卷积核大小kernal_size=k
转置卷积的运算步骤可以归为以下几步:
在输入特征图元素间填充s-1行、列0
在输入特征图四周填充k-p-1行、列0
将卷积核参数上下、左右翻转
做正常卷积运算(填充0,步距1)
转置卷积操作后特征图的大小可以通过如下公式计算:
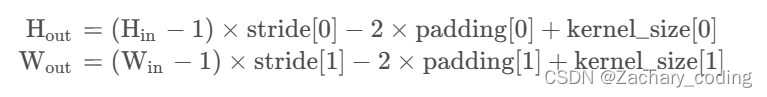






















 3150
3150











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








