链式前向星与邻接表对比

本文图片及数据

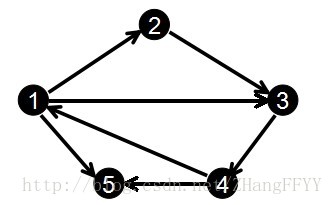
对于这样一张有向图：

输入边的顺序如下：
1 2
2 3
3 4
1 3
4 1
1 5
4 5

对于邻接表来说是这样的：
1 -> 2 -> 3 -> 5
2 -> 3
3 -> 4
4 -> 1 -> 5
5 ->^

对于链式前向星来说是这样的：

edge[0].to = 2; edge[0].next = -1; head[1] = 0;
edge[1].to = 3; edge[1].next = -1; head[2] = 1;
edge[2].to = 4; edge[2],next = -1; head[3] = 2;
edge[3].to = 3; edge[3].next = 0; head[1] = 3;
edge[4].to = 1; edge[4].next = -1; head[4] = 4;
edge[5].to = 5; edge[5].next = 3; head[1] = 5;
edge[6].to = 5; edge[6].next = 4; head[4] = 6;

（以起点为1举例）:
head[1] = 5 （以1为起点的第一条边的位置） -> edge[5].to = 5 （终点） -> edge[5].next = 3（同一起点下一条边的位置） ->edge[3].to = 3（第二条边的终点） -> edge[3].next = 0 -> edge[0].to = 2(第三条边的终点） ->edge[0].next = -1 （没下一条边）

简化来说就是：
1 -> 5 -> 3 -> 2
可以看到链式前向星和邻接表除了顺序不一样，其他的可以说是一样的。

看一下链式前向星的代码：

const int maxn = 10005;   //点的最大个数

int head[maxn], cnt=0;//head用来表示以i为起点的第一条边存储的位置，cnt读入边的计数器

struct Edge
{
    int next; //同一起点的上一条边的储存位置
    int to; //第i条边的终点
    int w; //第i条边权重
};
Edge edge[maxn];

void add(int u,int v,int w)  //读入边
{
    edge[cnt].w = w;
    edge[cnt].to = v;
    edge[cnt].next = head[u];
    head[u] = cnt++;
}

void read()  //遍历所有边
{
    for(int i=0; i<=n; i++)
        for(int j=head[i]; j！=-1; j=edge[j].next)
}

我觉得链式前向星和邻接表的思想是一样的，区别就是：邻接表是用链表实现的，可以动态的增加边，
而链式前向星是用结构体数组实现的，是静态的，需要一开始知道数据范围，开好数组大小。
相比之下，邻接表灵活，链式前向星好写。

如有理解不对的地方，希望可以告诉我。