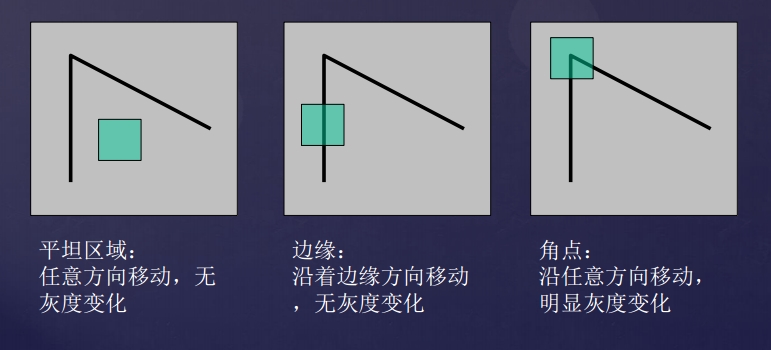
好的点特征如图1所示,在角点处,图像上的一个小窗口沿任何方向移动,窗口内的图像都有明显的灰度变化,因此角点是好的点特征。
图1
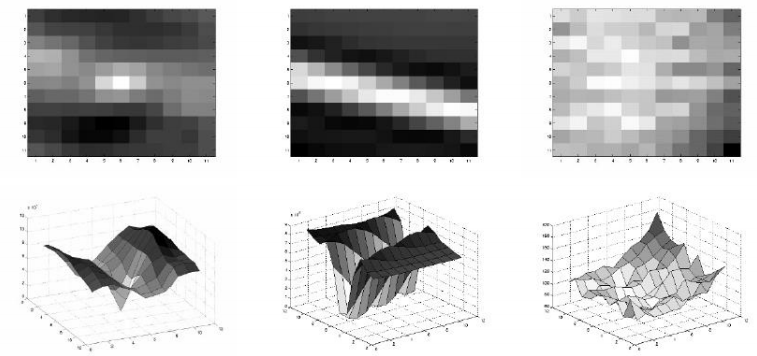
那么,我们要怎样识别角点呢?由图2可以看出,角点具有类似图2中的第一列所展示的性质:
图2
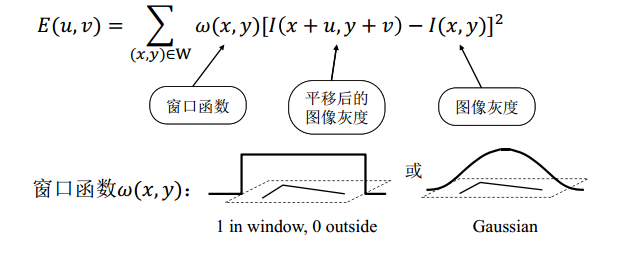
假设窗口W发生位置偏移(u,v);比较偏移前后窗口中每一个像素点的灰度变化值;使用灰度误差平方和来构造一个误差函数E(u,v),其中的窗口函数是用来滤波的。
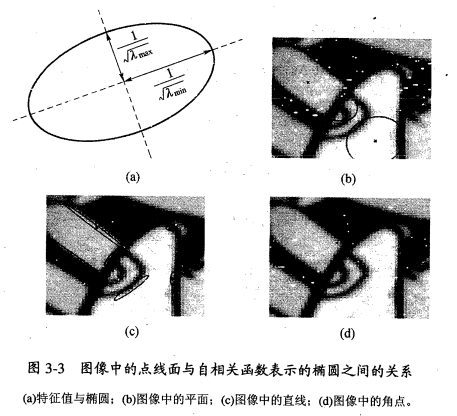
H称为自相关矩阵, λmax和λmin是自相关矩阵的特征值。其中E(u,v)是一个二次型函数,二次型函数的本质就是一个椭圆,椭圆的扁率和尺寸是由H的特征λmax和λmin值λmax和λmin决定的,椭圆的方向由H的特征向量决定。图3-3表示的是点线面与椭圆的关系,其中(d)图中的椭圆跑哪去了,我也不知道。因为图是从扫描版的PDF中截取的,有点模糊。
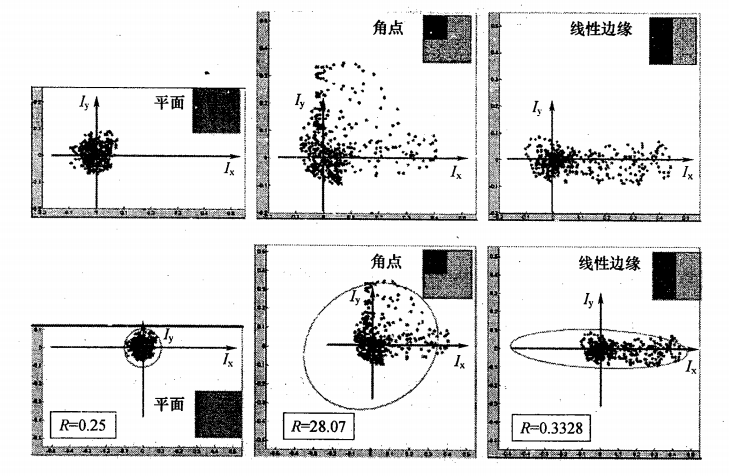
下面这幅图是王永明等在《图像局部不变性特征与描述》一书中阐述椭圆与点线面的关系用的。第一行是不同典型图像的灰度梯度分布图,第二行是对梯度分别的椭圆拟合。不过有一点没有明白,如果按照哈里斯的理论线性边缘时,R不应该为负值的吗?那王永明的这幅图中的R代表什么含义啊到底?为什么线性边缘时,R=0.3328?搞不懂啊搞不懂!!!
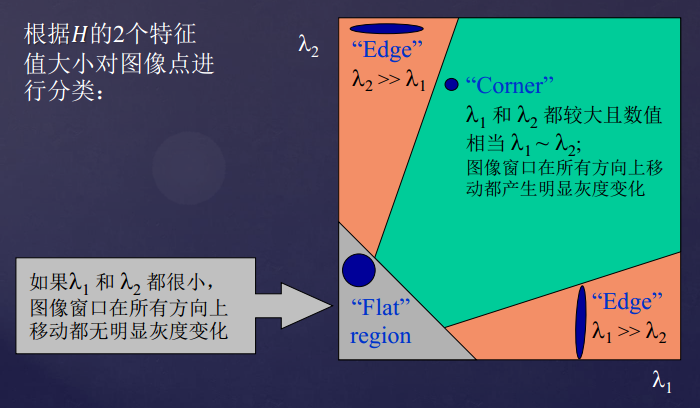
正如图3所示,只有当两者都比较大,并且大小相当时对应点才为角点,两者都非常小时为平坦区域;一大一小时为边界。
图3
在1988年,哈里斯在其论文《A combined corner and edge detector》里给出了更有效的角点响应函数
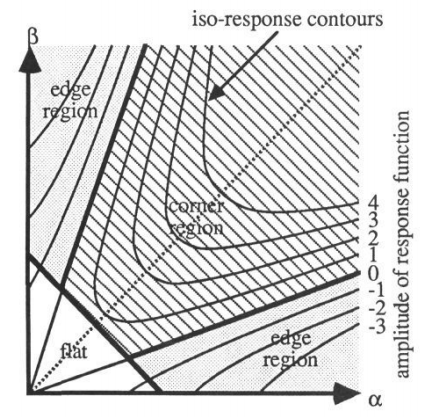
R为正值时,检测到的是角点;R为负时检测到的是边;R很小时检测到的是平坦区域,由此也就有了更便于计算的数学公式。哈老先生对此做的图如下:
下面是对Harris算法的Matlab实现,源码参考自http://blog.csdn.net/aflyeagle/article/details/5116799
个人对一些地方做了修改说明。
运行环境windows8.1+Matlab R2013b
%%%Prewitt Operator Corner Detection.m
%%%时间优化--相邻像素用取差的方法求Harris角点
%%
clear;
Image = imread('884.jpg'); % 读取图像
Image = im2uint8(rgb2gray(Image));
dx = [-1 0 1;-1 0 1;-1 0 1]; %dx:横向Prewitt差分模版
Ix2 = filter2(dx,Image).^2;
Iy2 = filter2(dx',Image).^2;
Ixy = filter2(dx,Image).*filter2(dx',Image);
%生成 9*9高斯窗口。窗口越大,探测到的角点越少。
h= fspecial('gaussian',9,2);
A = filter2(h,Ix2); % 用高斯窗口差分Ix2得到A
B = filter2(h,Iy2);
C = filter2(h,Ixy);
nrow = size(Image,1);
ncol = size(Image,2);
Corner = zeros(nrow,ncol); %zeros用来产生一个全零矩阵,故矩阵Corner用来保存候选角点位置,初值全零,值为1的点是角点
%参数t:点(i,j)八邻域的“相似度”参数,只有中心点与邻域其他八个点的像素值之差在
%(-t,+t)之间,才确认它们为相似点,相似点不在候选角点之列
t=20;
%我并没有全部检测图像每个点,而是除去了边界上boundary个像素,也就是从第8行第8列开始遍历。
%因为我们感兴趣的角点并不出现在边界上
%个人觉得这一部分是的主要目的是找出可能是角点的点,缩小范围,加快运算速度。
%具体思想是如果中心点(i,j)周围8个点中有7、8个点灰度值与之相似,那么该中心点应该处于平坦区域,不可能为角点,
%如果中心点(i,j)周围只有1个点或者没有点与之相似,那么该中心点也不可能为角点。
boundary=8;
for i=boundary:nrow-boundary+1
for j=boundary:ncol-boundary+1
nlike=0; %相似点个数
if Image(i-1,j-1)>Image(i,j)-t && Image(i-1,j-1)<Image(i,j)+t
nlike=nlike+1;
end
if Image(i-1,j)>Image(i,j)-t && Image(i-1,j)<Image(i,j)+t
nlike=nlike+1;
end
if Image(i-1,j+1)>Image(i,j)-t && Image(i-1,j+1)<Image(i,j)+t
nlike=nlike+1;
end
if Image(i,j-1)>Image(i,j)-t && Image(i,j-1)<Image(i,j)+t
nlike=nlike+1;
end
if Image(i,j+1)>Image(i,j)-t && Image(i,j+1)<Image(i,j)+t
nlike=nlike+1;
end
if Image(i+1,j-1)>Image(i,j)-t && Image(i+1,j-1)<Image(i,j)+t
nlike=nlike+1;
end
if Image(i+1,j)>Image(i,j)-t && Image(i+1,j)<Image(i,j)+t
nlike=nlike+1;
end
if Image(i+1,j+1)>Image(i,j)-t && Image(i+1,j+1)<Image(i,j)+t
nlike=nlike+1;
end
if nlike>=2 && nlike<=6
Corner(i,j)=1;%如果周围有2~6个相似点,那(i,j)就是角点
end;
end;
end;
CRF = zeros(nrow,ncol); % CRF用来保存角点响应函数值,初值全零
CRFmax = 0; % 图像中角点响应函数的最大值,作阈值之用
k=0.05;
% 计算CRF
%工程上常用CRF(i,j) =det(M)/trace(M)计算CRF,那么此时应该将下面第105行的
%比例系数k设置大一些,k=0.1对采集的这几幅图像来说是一个比较合理的经验值
for i = boundary:nrow-boundary+1
for j = boundary:ncol-boundary+1
if Corner(i,j)==1 %只关注候选点
M = [A(i,j) C(i,j);
C(i,j) B(i,j)];
CRF(i,j) = det(M)-k*(trace(M))^2;
if CRF(i,j) > CRFmax
CRFmax = CRF(i,j);
end;
end
end;
end;
%CRFmax
count = 0; % 用来记录角点的个数
t=0.01;
% 下面通过一个3*3的窗口来判断当前位置是否为角点
for i = boundary:nrow-boundary+1
for j = boundary:ncol-boundary+1
if Corner(i,j)==1 %只关注候选点的八邻域
if CRF(i,j) > t*CRFmax && CRF(i,j) >CRF(i-1,j-1) ......%?????为什么要CRF(i,j) > t*CRFmax啊?求大神告知
&& CRF(i,j) > CRF(i-1,j) && CRF(i,j) > CRF(i-1,j+1) ......
&& CRF(i,j) > CRF(i,j-1) && CRF(i,j) > CRF(i,j+1) ......
&& CRF(i,j) > CRF(i+1,j-1) && CRF(i,j) > CRF(i+1,j)......
&& CRF(i,j) > CRF(i+1,j+1)
count=count+1;%这个是角点,count加1
else % 如果当前位置(i,j)不是角点,则在Corner(i,j)中删除对该候选角点的记录
Corner(i,j) = 0;
end;
end;
end;
end;
% disp('角点个数');
% disp(count)
figure,imshow(Image); % display Intensity Image
hold on;
% toc(t1)
for i=boundary:nrow-boundary+1
for j=boundary:ncol-boundary+1
column_ave=0;
row_ave=0;
k=0;
if Corner(i,j)==1
for x=i-3:i+3 %7*7邻域
for y=j-3:j+3
if Corner(x,y)==1
% 用算数平均数作为角点坐标,如果改用几何平均数求点的平均坐标,对角点的提取意义不大
row_ave=row_ave+x;
column_ave=column_ave+y;
k=k+1;
end
end
end
end
if k>0 %周围不止一个角点
plot( column_ave/k,row_ave/k ,'g.');
end
end;
end;
采用国际会议中心的图片进行实验,效果如下:
原图:
标记效果图:
为了验证Harris的旋转不变性,将原图旋转后实验效果如下:








 本文详细介绍了Harris角点检测算法的工作原理及其在图像处理中的应用。通过对图像进行预处理并运用数学公式计算角点响应函数,该算法能够准确识别图像中的角点特征。此外,还提供了Matlab实现代码及实验结果分析。
本文详细介绍了Harris角点检测算法的工作原理及其在图像处理中的应用。通过对图像进行预处理并运用数学公式计算角点响应函数,该算法能够准确识别图像中的角点特征。此外,还提供了Matlab实现代码及实验结果分析。
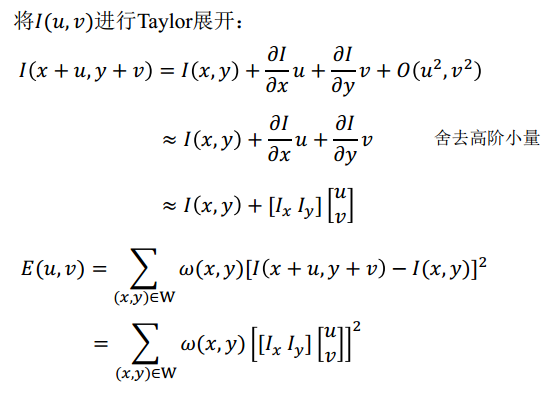
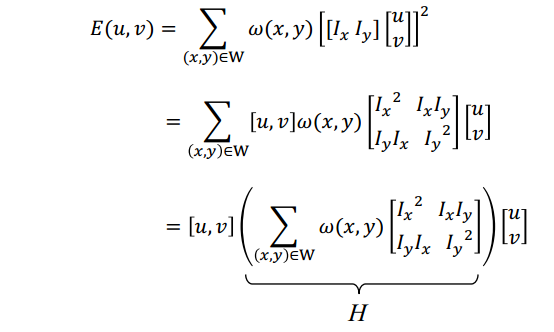
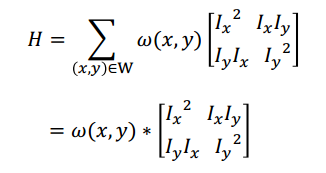
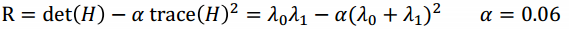




















 384
384

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








