C++求平面最近点对

引入

题目很好理解：给你N个点，求其中距离最近的一对点（之间的距离）。

很显然可以枚举，时间复杂度$\Theta \left({N}^{2} \right)$

如果数据强一点（N=100000什么的），显然枚举直接挂掉，那么要怎么办呢？
这里就要用到分治（当然是二分）了，时间复杂度$\Theta \left(N{{log}_{2}N}\right)$

Ps.以前几乎没做过分治，一来就碰到求最近点对这种题，我当时也看了1小时的题解才大概明白，当然我相信这篇博客一定能让你明白的~

算法

怎么分

首先，我们随便来几个点：

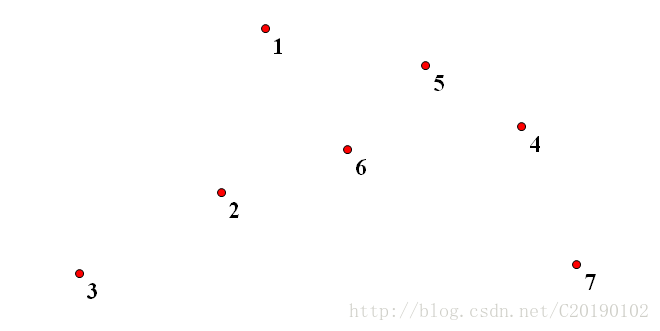
然后，将他们按x坐标排个序，方便找x坐标在中间的点，即编号为N/2的点。否则，例如上图，编号N/2（即3）的点根本不在中间。
排序过后编号所对应的点就不同了，也可以理解为点的编号不同了，即：

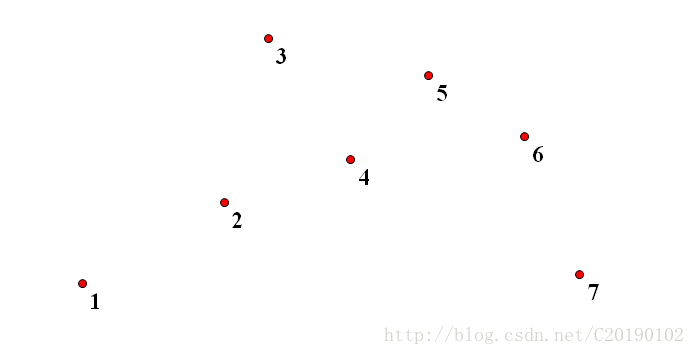
这样一来，想找x坐标中间的点就是N/2了（虽然不能整除，但没有问题）。
然后就可以直接由编号在中间的点二分了：

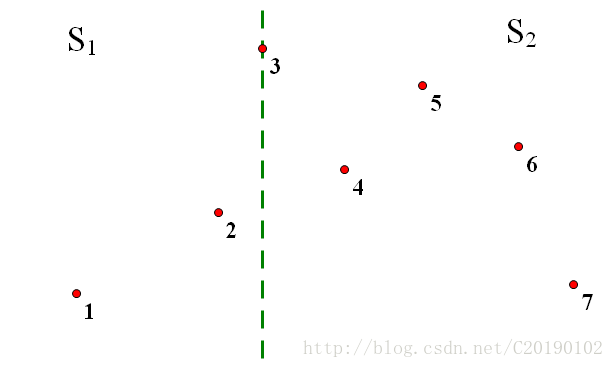
在S1里面重复上述的操作（排序就不用了），直到只有1个点时，返回极大值（点对不可能只有一个点），有两个点时，返回这两点的距离，很好理解。
然后再在S2里重复一次。
（这里的分治有递归的思想，实在无法理解的小伙伴自己多想想吧~我也没有什么办法讲得更详细了……）

怎么合

在得到S1和S2的答案后（当你递归到S1只有1个或2个点，S2也只有1个或2个点时，就需要从S1和S2的答案得到整体的答案了），首先想到：答案有可能是$min(Ans_{S_{1}},Ans_{S_{2}})$，这样就是算左右区间中更小的答案。

但是，这只是ans中的两个点都在一侧（S1或S2）的情况，但是ans有可能一个点在S1中，一个点在S2，这就是这道题最最最恶心的一个地方了

Ps.接下来的一切极其烧脑，做好准备吧骚年

设$d=min(Ans_{S_{1}},Ans_{S_{2}})$，则距离有可能小于d的两个点P1,P2只有可能在下图中的黑色直线之间：
图1
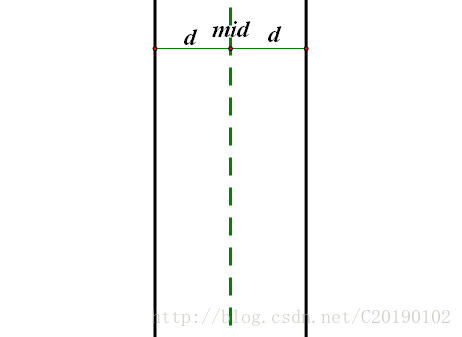
那我就要问（当时这个问题我想了好久，真的不明白）了：为什么不是在这个黑色直线之间呢？
图2
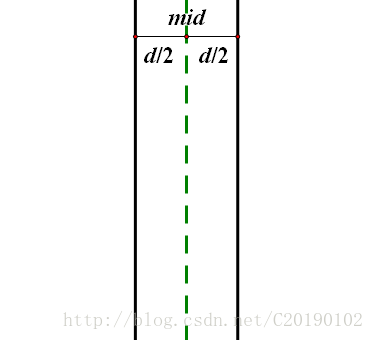
事实上，P1和P2两个点可以是这样的：
图3
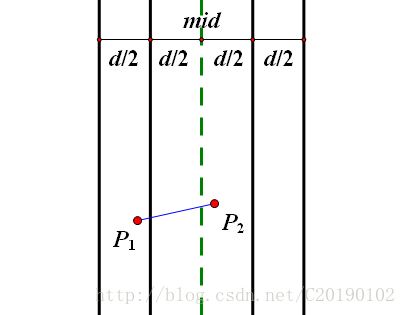
显然P1和P2的距离是小于d的，但P1并不在图2的范围内

好了，所以还需要把x坐标在 $mid_x-d$ 到 $mid_x+d$ 的点给挑出来。

然后怎么办？一个一个地枚举吗？还是不行，这样最坏的情况下可能会枚举到${(\frac{N}{2})}^2$个点（这个你可以不用知道为什么，只需要知道这样很耗时就行了）

所以我们还需要优化一下，网上很多人说，对于点P1，和它的距离小于d的最多只有6个点，但我完全不懂，所以这里就不这样了。我们可以用这一条优化：先将之前说的范围中的点挑出来后，按y坐标从小到大排序，然后两个循环枚举，但是，对于第二个点j，只要从第一个点i+1开始枚举即可。然后，当点j与点i的距离大于了d时，就不用再枚举j了（再枚举j的y坐标只会更大，与i的距离也会更大）。

算法就是这样了。

代码

见【分治】【二分】POJ 3714 Raid