Matrix Operations
这些函数操作的实现里面,我没有用一个Class抽象矩阵之后,再做操作实现.
关键还是希望减少阅读"困难".
如果你看到这篇笔记贴,希望不管感兴趣哪种操作实现,都可以很快的从Python内置数据结构入手,不用关心抽象.把注意力都集中在算法实现上面.
目前很多只是算法实现,还有时间复杂度高的值得优化的地方...
但是能用...
特比特别注意,这里有些函数实现的时候,我调用了,transpose这个转置的实现.
因为数学领域里面,总是喜欢用列向量 column vector,然后实际上Python实现的时候是很不方面对列向量做计算的.于是我有时候会使用转置,使之变成行向量,来进行计算会方便的多.
当你遇到坑爹又装逼的矩阵运算的表怕,一切都是纸老虎!
目前实现的主要矩阵操作:
Transpose +Determinant + Adjugate+ Inverse + Gram-Schimidt +LUP decomnposition + QR decomposition
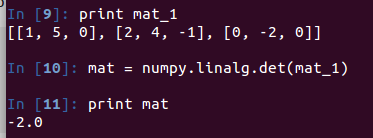
Determinant : 行列式求值
对于行列式求值,我实现了一个函数determinant(),用来求给定行列式的.
def determinant(self, matrix) :
row = len(matrix)
col = len(matrix[0])
if row == 1 :
return matrix
elif row == 2 :
return matrix[0][0]*matrix[1][1] - matrix[1][0] * matrix[0][1]
ret_val = 0
for i in range(0, col) :
tmp_mat = [[0 for x in range(0, col-1)] for y in range(0, row-1)]
for m in range(0, row-1) :
n = 0
while n < col-1 :
if n < i :
tmp_mat[m][n] = matrix[m+1][n]
else :
tmp_mat[m][n] = matrix[m+1][n+1]
n += 1
ret_val += ((-1)**(i)) * matrix[0][i] * \
self.determinant(tmp_mat)
return ret_valPython 的numpy模块有内嵌的行列式求值函数det()
Dot Product:点积
骚年啊!醒醒啊!你肿么可以把点积和内积弄混!!!
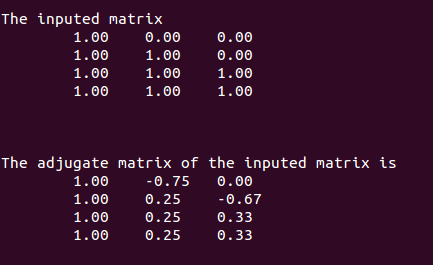
The Gram-Schimidt Process : 正交化
这里有一篇关于讨论Gram-Schimidt的文章,我觉得蛮好的:
http://cavern.uark.edu/~arnold/4353/CGSMGS.pdf
老实说,这里被坑了好久...看到一个资料上面
http://www.math.iit.edu/~fass/477577_Chapter_4.pdf
MIT的lecture
提供了一下算法.但是又没讲请促.我还以为q*是求伴随矩阵.坑我好久...我还去写了伴随矩阵的实现,
简直气愤...别看下面这个实现.越看越不相信自己...建议可以看我的Python实现...
我自己根据公式给出的Python实现:
def gram_schimidt(self, A) :
if A is None :
return
A_T = self.transpose(A)
row = len(A_T)
col = len(A_T[0])
V = [[0 for i in range(0, col)] for j in range(0, row)]
for i in range(0, row) :
tmp_mat = [0 for x in range(0, col)]
for j in range(0, col) :
tmp = A_T[i][j]
for k in range(0, i) :
factor = (1.0*self.dot_product(A_T[i], V[k])) / \
self.dot_product(V[k], V[k])
tmp -= factor*V[k][j]
V[i][j] = tmp
V = self.transpose(V)
return V
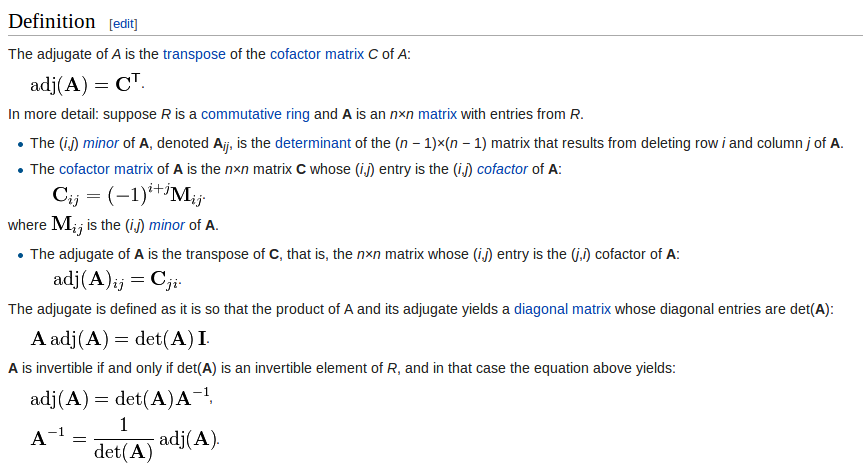
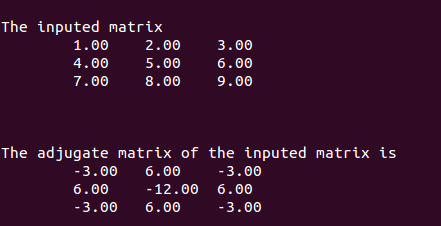
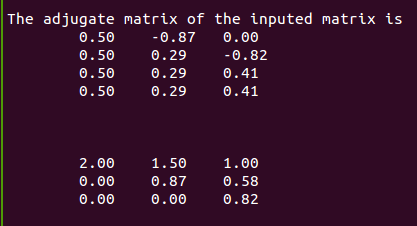
Adjugate:伴随矩阵
测试结果:
Inverse : 矩阵求逆
基于行列变换去做矩阵求逆
这里我实现了函数inverse(matrix),用来求解,给定参数matrix
最后我测试的时候让逆矩阵和原来的矩阵做矩阵乘法.最后得到单位矩阵.经检验,求逆算法是正确的.
def inverse(self, mat) :
if mat is None :
return
# make sure that this matrix that you inputed is invertible
if self.determinant(mat) == 0 :
print "ATTENTION! The determinant of matrix is ZERO"
print "This matrix is uninvertible"
return
row = len(mat)
col = len(mat[0])
#matrix = copy.copy(mat)
matrix = copy.deepcopy(mat)
# matrix = [[0 for i in range(0, col)] for j in range(0, row)]
# for i in range(0, row) :
# for j in range(0, col) :
# matrix[i][j] = mat[i][j]
for i in range(0, row) :
for j in range(0, col) :
if i == j :
matrix[i] += [1]
else :
matrix[i] += [0]
row = len(matrix)
col = len(matrix[0])
for i in range(0, row) :
if matrix[i][i] is 0 :
for k in range(i+1, row) :
if matrix[k][i] is not 0 :
break
if k is not i+1 :
for j in range(0, col) :
matrix[i][j], matrix[k][j] = matrix[k][j], matrix[i][j]
for k in range(i+1, row) :
if matrix[k][i] is not 0 :
times = (1.0*matrix[k][i])/matrix[i][i]
for j in range(i, col) :
matrix[k][j] /= times
matrix[k][j] -= matrix[i][j]
for i in range(0, row) :
for j in range(i+1, col/2) :
if matrix[i][j] is not 0 :
times = matrix[i][j]/matrix[j][j]
for k in range(j, col) :
matrix[i][k] -= times * matrix[j][k]
for i in range(0, row) :
times = matrix[i][i]
for j in range(0, col) :
matrix[i][j] /= times
output = [[0 for i in range(0, col/2)] for j in range(0, row)]
for i in range(0, row) :
for j in range(0, col/2) :
output[i][j] = matrix[i][j+col/2]
return output
QR decomposition :
这个在我原来看来装逼度很高的矩阵分解也就是个纸老虎
首先对其进行Gram-schimidt正交化处理,然后就简答鸟,看下面这个运算demo
向量组v由正交化过程求得,然后每个列向量除以自己的模值即可得到矩阵Q
利用Q是正交阵的特点,求得R矩阵
哥们儿,别忘记鸟,计算机求解的都是数值解,数值解不一定等于解析解~!
def qr_decomposition(self, A) :
if A is None :
return
orthogonal_mat = self.transpose(self.gram_schimidt(A))
row = len(orthogonal_mat)
col = len(orthogonal_mat[0])
Q = [[0 for i in range(0, col)] for j in range(0, row)]
for i in range(0, row) :
mag = self.magnitude(orthogonal_mat[i])
for j in range(0, col) :
Q[i][j] = orthogonal_mat[i][j]/mag
R = self.multiply(Q, A)
Q = self.transpose(Q)
return (Q, R)
关于LUP的理论分析去看CLRS吧.... 这里仅贴出自己的实现.
终于~ LUP不再那么神乎其神...


Eigen value and eigen vector :
看这里:
http://blog.csdn.net/cinmyheart/article/details/44086369
---------------
Python 实现:
"""
Programmer : EOF
Code date : 2015.02.28
Code file : matrix.py
Code description :
@transpose : return a matrix @A_T which is tranposed matrix of @A
@lu_decomposition : return matrix @L and @U which are decomposed from matrix @A
@plu_decomposition : return matrix @P, @L and @U which are decomposed from matrix @A
"""
import copy
import numpy
class mat() :
def transpose(self, A) :
row = len(A)
col = len(A[0])
A_T = [[0 for i in range(0, row)] for j in range(0, col)]
for i in range(0, row) :
for j in range(0, col) :
A_T[j][i] = A[i][j]
return A_T
def add(self, A, B) :
if A is None or B is None :
return
row_A = len(A)
col_A = len(A[0])
row_B = len(B)
col_B = len(B[0])
if row_A != row_B or col_A != col_B :
print "Are you kidding me? The matrixes that you inputed ",\
"have different size. It's illegal to add these matries together"
return
output = [[0 for i in range(0, col_A)] for j in range(0, row_A)]
for i in range(0, row_A) :
for j in range(0, col_A) :
output[i][j] = A[i][j] + B[i][j]
return output
def sub(self, A, B) :
if A is None or B is None :
return
row_A = len(A)
col_A = len(A[0])
row_B = len(B)
col_B = len(B[0])
if row_A != row_B or col_A != col_B :
print "Are you kidding me? The matrixes that you inputed ",\
"have different size. It's illegal to sub these matries together"
return
output = [[0 for i in range(0, col_A)] for j in range(0, row_A)]
for i in range(0, row_A) :
for j in range(0, col_A) :
output[i][j] = A[i][j] - B[i][j]
return output
def multiply(self, A, B) :
if A is None or B is None :
return
if len(A[0]) is not len(B) :
print "The size of the two inputed matrix is illegally ",\
"to do multiplication in matrix"
return
row_A = len(A)
col_A = len(A[0])
col_B = len(B[0])
output = [[0 for i in range(0, col_B)] for j in range(0, row_A)]
for i in range(0, row_A) :
for j in range(0, col_B) :
sum_val = 0
for k in range(0, col_A) :
sum_val += A[i][k] * B[k][j]
output[i][j] = sum_val
return output
def dot_product(self, A, B) :
if A is None or B is None :
return
len_A = len(A)
len_B = len(B)
if len_A != len_B :
print "It's Illegal to do dot product with the two matrixes",
"which have different size"
return
sum_val = 0
for i in range(0, len_A) :
sum_val += A[i]*B[i]
return sum_val
def magnitude(self, A) :
ret_val = self.dot_product(A, A)
return numpy.sqrt(ret_val)
def gram_schimidt(self, A) :
if A is None :
return
A_T = self.transpose(A)
row = len(A_T)
col = len(A_T[0])
V = [[0 for i in range(0, col)] for j in range(0, row)]
for i in range(0, row) :
tmp_mat = [0 for x in range(0, col)]
for j in range(0, col) :
tmp = A_T[i][j]
for k in range(0, i) :
factor = (1.0*self.dot_product(A_T[i], V[k])) / \
self.dot_product(V[k], V[k])
tmp -= factor*V[k][j]
V[i][j] = tmp
V = self.transpose(V)
return V
def adjugate(self, A) :
row = len(A)
col = len(A[0])
output = [[0 for x in range(0, col)] for y in range(0, row)]
for i in range(0, row) :
for j in range(0, col) :
tmp_mat = [[0 for x in range(0, col-1)] for y in range(0, row-1)]
for m in range(0, row) :
for n in range(0, col) :
if m < i and n < j :
tmp_mat[m][n] = A[m][n]
elif m > i and n < j :
tmp_mat[m-1][n] = A[m][n]
elif m < i and n > j :
tmp_mat[m][n-1] = A[m][n]
elif m > i and n > j :
tmp_mat[m-1][n-1] = A[m][n]
det_val = self.determinant(tmp_mat)
det_val *= (-1)**(i+j)
output[i][j] = det_val
output = self.transpose(output)
return output
def qr_decomposition(self, A) :
if A is None :
return
orthogonal_mat = self.transpose(self.gram_schimidt(A))
row = len(orthogonal_mat)
col = len(orthogonal_mat[0])
Q = [[0 for i in range(0, col)] for j in range(0, row)]
for i in range(0, row) :
mag = self.magnitude(orthogonal_mat[i])
for j in range(0, col) :
Q[i][j] = orthogonal_mat[i][j]/mag
R = self.multiply(Q, A)
Q = self.transpose(Q)
return (Q, R)
def lup_solve(self, L, U, pi, b) :
n = len(self.L)
x = [0 for i in range(0, n)]
y = [0 for i in range(0, n)]
for i in range(0, n) :
tmp = 0
for j in range(0, i-1) :
tmp += L[i][j] * y[j]
y[i] = b[ pi[i] ] - tmp
for i in range(n-1, -1, -1) :
tmp = 0
for j in range(i+1, n) :
tmp += U[i][j] * x[j]
x[i] = (y[i] - tmp)/u[i][i]
return x
def lu_decomposition(self, A) :
n = len(A)
a = A
self.L = [[0 for i in range(0, n)] for j in range(0, n)]
self.U = [[0 for i in range(0, n)] for j in range(0, n)]
for k in range(0, n) :
self.U[k][k] = a[k][k]
for i in range(k+1, n) :
self.L[i][k] = a[i][k]/self.U[k][k]
self.U[k][i] = a[k][i]
for i in range(k+1, n) :
for j in range(k+1, n) :
a[i][j] = a[i][j] - self.L[i][k]*self.U[k][j]
return (self.L, self.U)
def lup_decomposition(self, A) :
n = len(A)
a = A
pi = [i for i in range(0, n)]
for k in range(0, n) :
p = 0
for i in range(k, n) :
if abs(a[i][k]) > p :
p = abs(a[i][k])
k_prime = i
if p is 0 :
print "singular matrix"
return
pi[k], pi[k_prime] = pi[k_prime], pi[k]
for i in range(0, n) :
a[k][i], a[k_prime][i] = a[k_prime][i], a[k][i]
for i in range(k+1, n) :
a[i][k] /= (a[k][k] * 1.0)
for j in range(k+1, n) :
a[i][j] -= a[i][k] * a[k][j]
self.P = [[ 0 for i in range(0, len(pi))] for j in range(0, len(pi))]
for i in range(0, len(pi)) :
self.P[i][ pi[i] ] = 1
self.L = [[0 for i in range(0, n)] for j in range(0, n)]
self.U = [[0 for i in range(0, n)] for j in range(0, n)]
row = len(self.L)
col = len(self.L[0])
for i in range(0, row) :
for j in range(0, col) :
if j < i :
self.L[i][j] = a[i][j]
elif j == i :
self.L[i][j] = 1
self.U[i][j] = a[i][j]
else :
self.U[i][j] = a[i][j]
return (self.P, self.L, self.U)
def determinant(self, matrix) :
row = len(matrix)
col = len(matrix[0])
if row == 1 :
return matrix
elif row == 2 :
return matrix[0][0]*matrix[1][1] - matrix[1][0] * matrix[0][1]
ret_val = 0
for i in range(0, col) :
tmp_mat = [[0 for x in range(0, col-1)] for y in range(0, row-1)]
for m in range(0, row-1) :
n = 0
while n < col-1 :
if n < i :
tmp_mat[m][n] = matrix[m+1][n]
else :
tmp_mat[m][n] = matrix[m+1][n+1]
n += 1
ret_val += ((-1)**(i)) * matrix[0][i] * \
self.determinant(tmp_mat)
return ret_val
def inverse(self, mat) :
if mat is None :
return
# make sure that this matrix that you inputed is invertible
if self.determinant(mat) == 0 :
print "ATTENTION! The determinant of matrix is ZERO"
print "This matrix is uninvertible"
return
row = len(mat)
col = len(mat[0])
#matrix = copy.copy(mat)
matrix = copy.deepcopy(mat)
# matrix = [[0 for i in range(0, col)] for j in range(0, row)]
# for i in range(0, row) :
# for j in range(0, col) :
# matrix[i][j] = mat[i][j]
for i in range(0, row) :
for j in range(0, col) :
if i == j :
matrix[i] += [1]
else :
matrix[i] += [0]
row = len(matrix)
col = len(matrix[0])
for i in range(0, row) :
if matrix[i][i] is 0 :
for k in range(i+1, row) :
if matrix[k][i] is not 0 :
break
if k is not i+1 :
for j in range(0, col) :
matrix[i][j], matrix[k][j] = matrix[k][j], matrix[i][j]
for k in range(i+1, row) :
if matrix[k][i] is not 0 :
times = (1.0*matrix[k][i])/matrix[i][i]
for j in range(i, col) :
matrix[k][j] /= times
matrix[k][j] -= matrix[i][j]
for i in range(0, row) :
for j in range(i+1, col/2) :
if matrix[i][j] is not 0 :
times = matrix[i][j]/matrix[j][j]
for k in range(j, col) :
matrix[i][k] -= times * matrix[j][k]
for i in range(0, row) :
times = matrix[i][i]
for j in range(0, col) :
matrix[i][j] /= times
output = [[0 for i in range(0, col/2)] for j in range(0, row)]
for i in range(0, row) :
for j in range(0, col/2) :
output[i][j] = matrix[i][j+col/2]
return output
def eig(self, A) :
if A is None :
return
tmp_mat = copy.deepcopy(A)
for i in range(0, 20) :
(Q, R) = self.qr_decomposition(tmp_mat)
tmp_mat = self.multiply(R, Q)
row = len(tmp_mat)
col = len(tmp_mat[0])
for i in range(0, row) :
for j in range(0, col) :
if i != j :
tmp_mat[i][j] = 0
eig_vec = self.inverse(self.sub(A, tmp_mat))
return (tmp_mat, eig_vec)
def show(self, matrix) :
if matrix is None :
return
row = len(matrix)
col = len(matrix[0])
for i in range(0, row) :
for j in range(0, col) :
print "\t%1.2f" % matrix[i][j],
print
print "\n\n"
#-----------------for testing------------------------------------
#matrix = [[2,3,1,5], [6,13,5,19], [2,19,10,23],[4,10,11,31]]
matrix = [[2,0,2,0.6], [3,3,4,-2], [5,5,4,2], [-1,-2,3.4,-1]]
m = mat()
print "The determinant of matrix @mat_1 :"
mat_1 = [[1, 0, 0], [0, 2, 0], [0, 0, 3]]
m.show(mat_1)
print m.determinant(mat_1)
print "The determinant of matrix @mat_2 :"
mat_2 = [[1, 5, 0], [2, 4, -1], [0, -2, 0]]
m.show(mat_2)
print m.determinant(mat_2)
print "The input matrix is \n"
m.show(matrix)
print "After transpose\n"
m.show(m.transpose(matrix))
(P, L, U) = m.lup_decomposition(matrix)
print "After PLU decomposition, we got matrixes"
print "P:"
m.show(P)
print "L:"
m.show(L)
print "U:"
m.show(U)
inv_mat = m.inverse(matrix)
print "The inverse matrix of the inputed matrix is "
m.show(inv_mat)
print "Output"
m.show(m.multiply(inv_mat, matrix))
mat_1 = [[1,2,3],[4,5,6],[7,8,9]]
print "The inputed matrix"
m.show(mat_1)
print "The adjugate matrix of the inputed matrix is "
m.show(m.adjugate(mat_1))
mat_1 = [[1,0,0],[1,1,0],[1,1,1],[1,1,1]]
print "The inputed matrix"
m.show(mat_1)
print "The gram chimidt matrix of the inputed matrix is "
m.show(m.gram_schimidt(mat_1))
print "The inputed matrix"
m.show(mat_1)
print "The adjugate matrix of the inputed matrix is "
(Q, R) = m.qr_decomposition(mat_1)
m.show(Q)
m.show(R)
#mat_1 = [[2, 3], [3, -6]]
mat_1 = [[2, 1], [1, 2]]
print "The inputed matrix"
m.show(mat_1)
print "The eig value matrix of the inputed matrix is "
(eig_val, eig_vector) = m.eig(mat_1)
m.show(eig_val)
m.show(eig_vector)
waiting for updates ... ...
2015.02.28 更新了行列式求值的实现.determinant()
2015.03.01 更新了矩阵求逆的实现.inverse()
2015.03.03 更新了矩阵求伴随矩阵的实现adjugate()
2015.03.05 更新了矩阵Gram-Schimit()正交化的实现.
2015.03.05 更新了矩阵的QR分解的实现
2015.03.05 更新了矩阵的特征值和特征向量的实现eig()
再美好也经不住遗忘,再悲伤也抵不过时光
摄于二零一五年大年初二





































 3319
3319

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








