从零实现3D图像引擎：(10)Hello3DWorld

1. 数学分析

前面我们已经把预先想到的可能会用到的数学工具都封装好了，从这篇开始，应该很少出现一大篇都是数学推导的了，终于看见光明了，这次我们将开始第一个3D程序的编写，所以题目就叫Hello3DWorld吧。

 

0) 3D程序的本质

很多书都会先介绍“3D流水线”的词，但其实明白3D程序的人一下子就知道这是什么，而不了解的人看了这个词也没有意义。其实我也觉得没什么特殊意义，因为所有计算机程序都是一个一个流程执行下来的，不全都是某某流水线么。简单来说，3D流水线就是，从在计算机中表示三维世界的数据，到绘制到计算机2D屏幕上的整个过程。

 

3D流水线的子过程有很多，都列出来只能让人更迷惑，还是举个例子说个简单的情况吧：

(1) 首先，你的3D游戏什么也没有，只有一个空空的世界，它除了有X,Y,Z三个坐标以外，什么也没有。

(2) 你的手里有一个金字塔，如果在计算机中表示，则金字塔有自己的一套X,Y,Z坐标系，还有金字塔的四个尖端(顶点)在金字塔坐标系中的坐标。

(3) 你需要把金字塔放在游戏世界中，于是需要建立一个关系——金字塔坐标系中的原点，在游戏世界中的坐标是什么。

(4) 一旦这个关系找到了，就可以把金字塔的所有顶点都移动到游戏世界中去。

(5) 东西都放好了，怎么显示这个3D世界呢？不妨以我们自己来做例子，我们生活在三维世界中，我们看到的东西，就是要显示的东西。所以在游戏世界中，我们也需要一个类似眼睛的东西，我们管它叫另外一个名字——相机。

(6) 相机在游戏世界中，就好象我们人在现实世界中。人的位置不同、看的方向不同，那么眼睛里的景色也不同。所以，在游戏世界里，我们要给这个相机设置坐标，还有它的朝向，这样才能确定看到什么景色。

(7) 现在相机所看的是一个锥形的3D世界，锥形的尖的位置就是相机的坐标，锥形的底面积随着相机朝向的方向越来越大。

(8) 最后，我们把这个锥体内的景色都投影到一个2D平面上，并放在计算机屏幕上显示。

 

下面来对上面说的步骤分开详细说明。

 

 

1) 物体局部坐标->世界坐标

一张图足以说明：

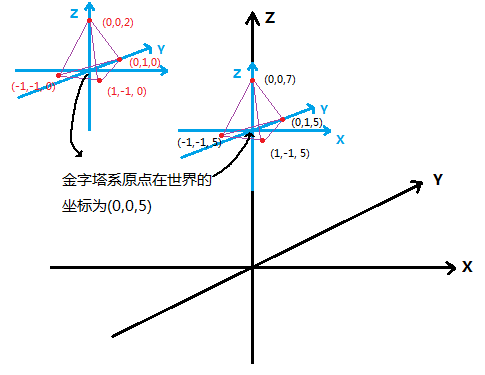
我们只要把物体的顶点的坐标的X,Y,Z都加上物体系原点在世界系下的坐标(0,0,5)，就可以得到物体的各顶点在世界系下的坐标了。

 

 

2) 世界坐标->相机坐标

下图展示了上面所说的视景椎体和相机在游戏世界中的作用，注意该图是俯视2D图，方便理解。还有这个物体和上图的金字塔不是一回事，这是一个普遍的物体和相机，坐标都是很随意的，没有上面的那么特殊。

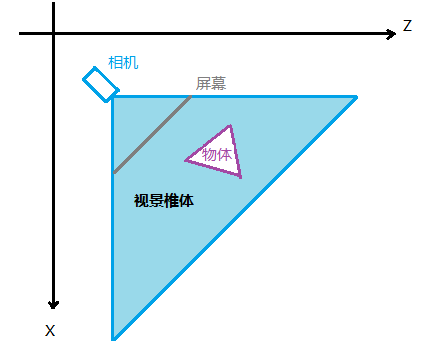
如上图，其实对于画在计算机屏幕上的目的而言，只有视景椎体内(屏幕后面的其实也没有用)的物体我们才关心，而且我们也实际上不关心物体在世界中的坐标，而只关心物体透视在屏幕上是什么坐标。这就引出了相机坐标系的概念，为了方便透视的运算，我们将建立相机坐标系，其中原点就是相机的位置，相机的朝向固定为正Z轴的方向，如下图：

这样，我们在做透视投影时如果知道了物体在相机坐标系下的坐标，透视运算将会非常的容易，这个下面会说到，现在我们先把物体挪过来吧。如下图所示，需要做两步操作：

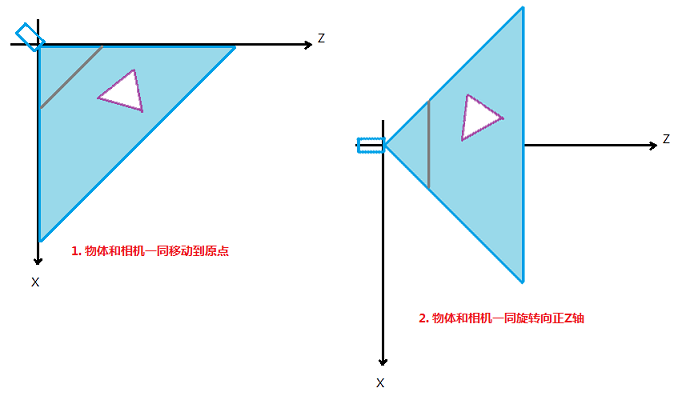
经过上述两部，物体的坐标就从世界坐标系转化到了相机坐标系中。这里要注意，我是将物体和相机一起移动到原点，这是因为要保持相机视景椎体内的景色不变，在相机移动到原点之后，相机在相机系的坐标就是(0,0,0)，朝向就是正Z轴，所以对相机不需要运算。需要运算的只有物体的顶点坐标，要算两次，一次是平移，一次是旋转。

 

(1) 物体平移到相机系

很显然，相机移动了多少，物体就移动了多少。所以我们要求一个(dx, dy, dz)，使得相机的坐标和这个(dx, dy, dz)相加为(0, 0, 0)，这样，我们只需要把物体的坐标与这个(dx, dy, dz)相加，也就能求得物体在相机系下的坐标了。

我们设相机在世界系下的坐标为(cx, cy, cz)，那么(dx, dy, dz)是多少呢？还用我说么。。。当然是(-cx, -cy, -cz)了。

所以，我们只要把物体在世界系下的坐标wx, wy, wz，分别减去相机在世界系下的坐标cx, cy, cz就好了，OK完成。

 

(2) 物体随相机旋转

说到这里有点郁闷，因为之前没有介绍向量与矩阵的转化和矩阵的几何意义，但在这个小节来做这个完整的推导只能让人更迷惑，所以对旋转矩阵的推导就作为下一篇的内容吧，这里先给出结果：

物体绕X、Y、Z轴分别旋转的变换矩阵：

R_x(theta) =

1 0 0

0 cos(theta) sin(theta)

0 -sin(theta) cos(theta)

 

R_y(theta) =

cos(theta) 0 -sin(theta)

0 1 0

sin(theta) 0 cos(theta)

 

R_z(theta) =

cos(theta) sin(theta) 0

-sin(theta) cos(theta) 0

0 0 1

 

只要用一个点向量乘以这个变换矩阵，得到的结果向量就是绕对应轴旋转theta度后的点向量了。

 

要注意的是，上面的矩阵都是物体旋转的矩阵，可是我们现在已知的是相机的朝向，所以在把物体转到相机系的过程中，物体顶点绕各个轴旋转的角度是和现在已知的相机朝向相反的，所以物体世界坐标->相机坐标的旋转过程要使用-theta代入到上面的矩阵中去才是正确的。

 

3) 透视投影

经过上面的操作，现在只差一步了，把视景椎体中的物体顶点透视投影到屏幕2D平面上来。其实特别简单，如下图：

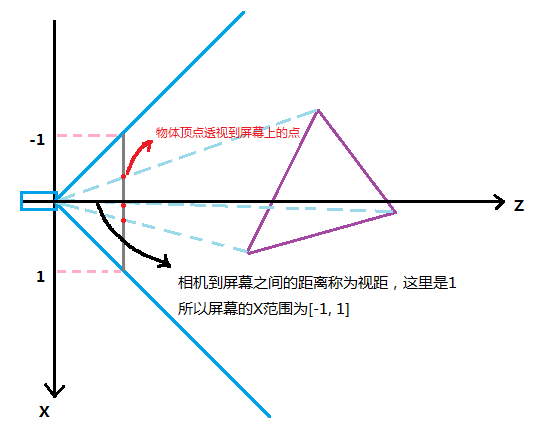
这里又是个俯视2D图，可以清楚的看到这个三角形的三个顶点是如何透视投影到屏幕上的。

下面的图则表明了透视后的点的X坐标怎么算：

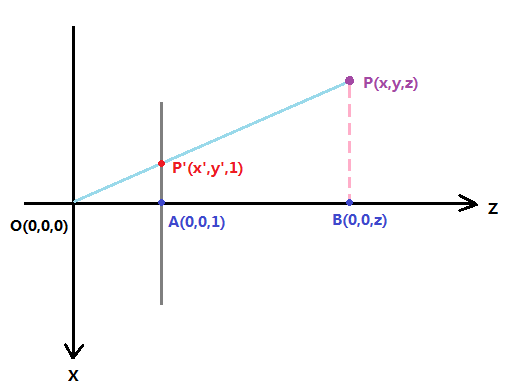
点P就是物体的某一个顶点，因为这个图是沿Y轴负方向俯视下来的，所以Y坐标在这里都无法显示，但因为Y与X的推导原理相同，所以只看这里的X，我们就可以得到结论。

投影后的点为P'，所以所求的x'就是线段AP，根据相似三角形的原理，可以非常容易得出：

AP' : BP = OA : OB

所以AP' = OA * BP / OB

好了，我们把坐标代进来吧：

x' = 视距 * x / z

如果我们将视距设置为1，那么x' = x / z，简单吧，而且整个视野内的物体的X坐标都将在[-1 , 1]这个范围内。

同理，y' = y / z。

 

4) 屏幕变换

就差最后一步了，我们现在x的范围是[-1, 1]，y的范围也是[-1, 1]，但是计算机屏幕的分辨率是800 * 600 (随便举个例子)，怎么转换呢？

先把负数去掉吧，我们给X和Y坐标都先加个1，于是范围就变成了[0, 2]了。

离终点很近了，我们再把X坐标乘以400，范围不就是[0, 800]了么。OK，X坐标解决了。

现在是Y坐标，你想把它乘以600？那你就想错了。还记得我们的相机拍下了什么吗？我们的相机拍出的照片是正方形的，但是现在你要把他完整的放在一个4:3的屏幕上，那里面的人不就被压扁了么？

 

这就和CCTV是一个道理，现在大家电视机都是16:9的，他还非要放4:3的视频源，现在看新闻，主持人全都是胖子了。

我们不能像他们一样愚蠢(开玩笑啦，CCTV也有自己的苦衷)，所以我们要让Y坐标也放大400，这样的图像才是还原的照片。但是问题就来了，现在我们的图像是800 * 800，怎么显示在800 * 600的屏幕上呢？

 

中国移动给了我们一个好答案——剪卡！如果SIM卡装不进去IPHONE，我们就把它剪了。

那么我们不要上面的100和下面的100了，～～OK，这不就变成800 * 600了么。

看下图一看便知～：

其实有更好的方法解决这个问题，就是给相机分别定义垂直、水平的视野，这样投影屏幕就有了宽高比的概念，这个我想以后在封装相机操作的时候再优化了，现在我们先用这种最易理解的方式来吧:)

 

 

 

2. 代码实现

1) 首先，我们定义几个数据结构用来表示我们的金字塔。

我们都知道3D物体在计算机中是用一个个多边形来表示的，其实所说的多边形就是三角形，每个三角形都有三个顶点，但是如果用这些三角形来表示金字塔的的话，就是4个面×每个面的3个顶点，一共是12个顶点，然而实际呢？一个金字塔就只有4个顶点和4个三角形，这些三角形有共用顶点的情况存在，所以我们定义一个顶点数组来保存这4个顶点，并且每个三角形都有一个长度为3的整型数组来保存它自己的三个顶点的索引。

typedef struct POLY_TYPE // 多边形(三角形)，通过顶点列表和索引描述 { POINT4D_PTR VertexList; // 顶点列表的指针 int VertexIndexs[3]; // 顶点在列表中的索引 } POLY, *POLY_PTR;

 

对于物体，需要保存组成该物体的POLY(三角形)的数组，还需要物体原点在世界系下的坐标：

typedef struct OBJECT_TYPE // 物体 { POINT4D WorldPos; // 世界坐标 int VertexCount; // 顶点数 POINT4D VertexListLocal[OBJECT_MAX_VERTICES]; // 物体顶点局部坐标数组 POINT4D VertexListTrans[OBJECT_MAX_VERTICES]; // 物体顶点变换后坐标数组 int PolyCount; // 多边形数 POLY PolyList[OBJECT_MAX_POLYS]; // 多边形数组 } OBJECT, *OBJECT_PTR;

您会发现我用了两个数组，我希望永远保留一份物体在执行变换前的局部顶点数据，如果只存一份的话，变换后将会覆盖掉，那么我们就无法根据最初的状态来执行其他变换了。

 

这里我还用了一个简单的相机结构来保存相机的世界坐标和朝向：

typedef struct CAMERA_TYPE // 相机 { POINT4D WorldPos; // 相机在世界的坐标 double AngelX, AngelY, AngleZ; // 相机的朝向，使用绕X,Y,Z轴分别转多少度来表示 } CAMERA, *CAMERA_PTR;

 

 

2) 现在写上面分析中介绍的那3步的三个函数，有了理论基础，实现总是那么随意而又简单：

void _CPPYIN_3DLib::ObjectWorldTransform(OBJECT_PTR obj) // 物体世界变换，使用VertexListLocal作为顶点数据源，顶点变换结果存放在VertexListTrans中 { for (int i = 0; i < obj->VertexCount; ++i) { VectorAdd(&(obj->VertexListLocal[i]), &(obj->WorldPos), &(obj->VertexListTrans[i])); } } void _CPPYIN_3DLib::ObjectCameraTransform(OBJECT_PTR obj, CAMERA_PTR camera) // 物体相机变换，使用VertexListTrans作为顶点数据源，顶点变换结果更新在VertexListTrans中 { // 先根据相机坐标平移物体，创建相机平移矩阵，再求逆获得物体的平移矩阵 MATRIX4X4 cameraMoveMatrix, objMoveMatrix; BuildMoveMatrix(&(camera->WorldPos), &cameraMoveMatrix); MatrixInverse(&cameraMoveMatrix, &objMoveMatrix); // 创建物体在相机变换中的旋转矩阵，其实就是物体旋转矩阵，但因为是相对于相机的，所以角度取负 MATRIX4X4 objRotateXMatrix = { 1, 0, 0, 0, 0, FastCos(-camera->AngelX), FastSin(-camera->AngelX), 0, 0, -FastSin(-camera->AngelX), FastCos(-camera->AngelX), 0, 0, 0, 0, 1 }; MATRIX4X4 objRotateYMatrix = { FastCos(-camera->AngelY), 0, -FastSin(-camera->AngelY), 0, 0, 1, 0, 0, FastSin(-camera->AngelY), 0, FastCos(-camera->AngelY), 0, 0, 0, 0, 1 }; MATRIX4X4 objRotateZMatrix = { FastCos(-camera->AngleZ), FastSin(-camera->AngleZ), 0, 0, -FastSin(-camera->AngleZ), FastCos(-camera->AngleZ), 0, 0, 0, 0, 1, 0, 0, 0, 0, 1 }; // 将这4个矩阵相乘合并为相机变换矩阵mt MATRIX4X4 m1, m2, mt; MatrixMul(&objMoveMatrix, &objRotateYMatrix, &m1); MatrixMul(&m1, &objRotateXMatrix, &m2); MatrixMul(&m2, &objRotateZMatrix, &mt); // 执行物体变换 ObjectTransform(obj, &mt, RENDER_TRANSFORM_TRANS, 0); } void _CPPYIN_3DLib::ObjectProjectTransform(OBJECT_PTR obj) // 透视变换，将3D坐标透视为2D坐标，结果为x取值为(-1,1)，Y取值为(-1, 1) { for (int i = 0; i < obj->VertexCount; ++i) { obj->VertexListTrans[i].x = obj->VertexListTrans[i].x / obj->VertexListTrans[i].z; obj->VertexListTrans[i].y = obj->VertexListTrans[i].y / obj->VertexListTrans[i].z; } }

 

 

3) 一个金字塔旋转的DEMO

有了上面的函数，我们可以构建一个金字塔，放置一个相机。先定义它们的数据存储：

POINT4D g_VertexList[4]; // 顶点数组 POLY g_Poly[4]; // 平面数组 OBJECT g_Obj; // 金字塔 CAMERA g_Camera; // 相机 int g_ObjRatationAngelZ = 0; // 金字塔旋转的角度，逐渐增加

 

在游戏初始化时，把他们的值设置好：

// 设置局部坐标 POINT4D v1 = { 0, 1, 0, 1 }; POINT4D v2 = { -1, -1, 0, 1 }; POINT4D v3 = { 1, -1, 0, 1 }; POINT4D v4 = { 0, 0, 2, 1 }; g_VertexList[0] = v1; g_VertexList[1] = v2; g_VertexList[2] = v3; g_VertexList[3] = v4; g_Poly[0].VertexList = g_VertexList; g_Poly[0].VertexIndexs[0] = 0; g_Poly[0].VertexIndexs[1] = 1; g_Poly[0].VertexIndexs[2] = 2; g_Poly[1].VertexList = g_VertexList; g_Poly[1].VertexIndexs[0] = 3; g_Poly[1].VertexIndexs[1] = 1; g_Poly[1].VertexIndexs[2] = 2; g_Poly[2].VertexList = g_VertexList; g_Poly[2].VertexIndexs[0] = 0; g_Poly[2].VertexIndexs[1] = 3; g_Poly[2].VertexIndexs[2] = 2; g_Poly[3].VertexList = g_VertexList; g_Poly[3].VertexIndexs[0] = 0; g_Poly[3].VertexIndexs[1] = 1; g_Poly[3].VertexIndexs[2] = 3; // 设置物体属性 g_Obj.PolyCount = 4; g_Obj.PolyList[0] = g_Poly[0]; g_Obj.PolyList[1] = g_Poly[1]; g_Obj.PolyList[2] = g_Poly[2]; g_Obj.PolyList[3] = g_Poly[3]; g_Obj.VertexCount = 4; g_Obj.VertexListLocal[0] = g_VertexList[0]; g_Obj.VertexListLocal[1] = g_VertexList[1]; g_Obj.VertexListLocal[2] = g_VertexList[2]; g_Obj.VertexListLocal[3] = g_VertexList[3]; POINT4D wp = { 0, 0, 5, 1 }; g_Obj.WorldPos = wp; // 设置相机 POINT4D cwp = { 0, 0, -1, 1 }; g_Camera.WorldPos = cwp; g_Camera.AngelX = 0; g_Camera.AngelY = 0; g_Camera.AngleZ = 0;

 

在游戏核心逻辑的地方，每次把角度转1度，当到了360度时，再变成0度，然后进行3个变换，生成屏幕坐标系下的4个顶点：

// 世界变换 ObjectWorldTransform(&g_Obj); // 每次旋转一下物体 ++g_ObjRatationAngelZ; if (g_ObjRatationAngelZ >= 360) g_ObjRatationAngelZ = 0; MATRIX4X4 objRotateZMatrix = { FastCos(g_ObjRatationAngelZ), FastSin(g_ObjRatationAngelZ), 0, 0, -FastSin(g_ObjRatationAngelZ), FastCos(g_ObjRatationAngelZ), 0, 0, 0, 0, 1, 0, 0, 0, 0, 1 }; ObjectTransform(&g_Obj, &objRotateZMatrix, RENDER_TRANSFORM_TRANS, 0); // 相机变换 ObjectCameraTransform(&g_Obj, &g_Camera); // 投影变换 ObjectProjectTransform(&g_Obj); // 放大到屏幕上 for (int i = 0; i < 4; ++i) { g_Obj.VertexListTrans[i].x *= SCREEN_WIDTH; g_Obj.VertexListTrans[i].x += (SCREEN_WIDTH / 2); g_Obj.VertexListTrans[i].y *= SCREEN_WIDTH; g_Obj.VertexListTrans[i].y += (SCREEN_WIDTH / 2) - 100; }

 

最后，把这4个点用之前我们写的Bresenham光栅化直线函数画出直线。这里我通过修改以前的函数写了一个画虚线的函数，然后把背面的三根直线画成了虚线：

// 绘制物体 DWORD color = ARGB(0,255,0,255); DrawLine(g_Obj.VertexListTrans[0].x, g_Obj.VertexListTrans[0].y, g_Obj.VertexListTrans[1].x, g_Obj.VertexListTrans[1].y, color); DrawLine(g_Obj.VertexListTrans[1].x, g_Obj.VertexListTrans[1].y, g_Obj.VertexListTrans[2].x, g_Obj.VertexListTrans[2].y, color); DrawLine(g_Obj.VertexListTrans[2].x, g_Obj.VertexListTrans[2].y, g_Obj.VertexListTrans[0].x, g_Obj.VertexListTrans[0].y, color); DrawVirtualLine(g_Obj.VertexListTrans[0].x, g_Obj.VertexListTrans[0].y, g_Obj.VertexListTrans[3].x, g_Obj.VertexListTrans[3].y, color, 5); DrawVirtualLine(g_Obj.VertexListTrans[1].x, g_Obj.VertexListTrans[1].y, g_Obj.VertexListTrans[3].x, g_Obj.VertexListTrans[3].y, color, 5); DrawVirtualLine(g_Obj.VertexListTrans[2].x, g_Obj.VertexListTrans[2].y, g_Obj.VertexListTrans[3].x, g_Obj.VertexListTrans[3].y, color, 5);

 OK，都完成了。

 

 

3. 源码下载

这次的DEMO截图如下：

 

完整项目下载地址：>>点击进入下载页<<

 

 

4. 补充内容

我们有太多的东西没有做了，主要有几个方面：

1) 从文件中读取3D数据，而不是我们手动来写。比如从3ds max的.3ds中读入数据。

2) 将世界中不在视景椎体中的物体移除掉，不对他们进行变换，浪费计算。

3) 视景椎体中太远和太近的东西，我们也不要。

4) 一半在椎体中，一半在锥体外的物体，我们要进行裁剪。

5) 我们的相机过于简单了，而且还有Gimbol lock问题，不过这个DEMO中可以达到要求了。

6) 光照处理

7) 消除背面没用的多边形

8) 贴图

……

太多了。

但不要着急，我们已经看到了第一个收获，一个可以随意修改的半成品线框渲染引擎和一个示例。