从零开始重写KOK1(万王之王1) —— (3)优化玩家移动与精确8方向朝向

0. 回顾与分析

在第1篇文章中，我们是对移动目标与玩家坐标做差，然后按照各个方向的可能性进行if判断，来决定人物的方向，在第一篇的DEMO中，可以发现，只有当人物正好在正斜方(45度的4个斜方向，或者说是n*pi/4时)，人物才会斜着站，否则都是上下左右4个方向的朝向。

 

对人物的移动方面，我们是x没达到目标则加上RunSpeed，y也如此。这样的结果是，人物斜着走将会非常快。

 

所以我们优化代码以达到两个目的：

(1)人物的朝向是将一个圆分成16份，每个方向占两份，使人物朝向正确的角度。

(2)人物的RunSpeed应当对应向量，让玩家在朝任意方向走时，移动速度是一致的。

 

首先是截图和下载地址，这个和上篇文章是相同的：

 

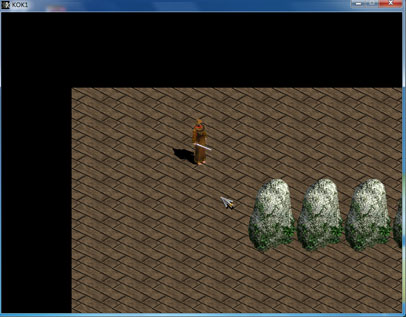
直接可运行版本下载：>>点击进入下载页<<

 

1. 优化玩家朝向

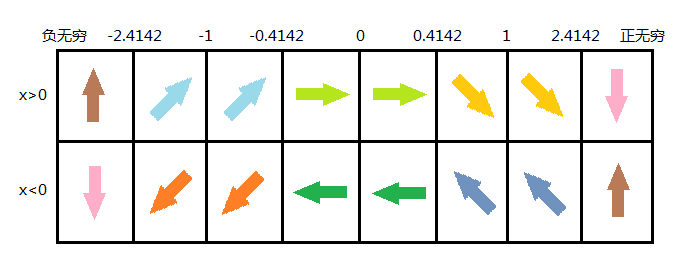
首先画个图，来想象一下，什么情况应该朝哪个方向：

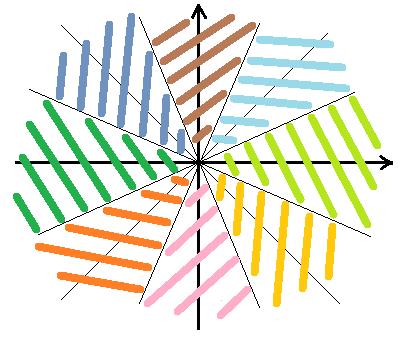
每个颜色代表一个方向，玩家在相同颜色的区域内应该朝向相应的方向。在这个图中轴x的正方向是0，从正方向延逆时针旋转到x轴的负方向的弧度为pi，从x轴的正方向延顺时针旋转到x轴的负方向的弧度为-pi。但要注意到，在游戏中，y轴的正方向是向下的，将y轴方向颠倒，把弧度注释在图上即如下图：

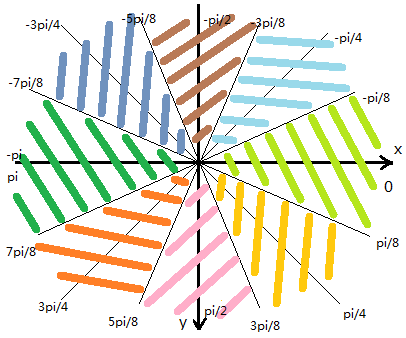
好了，那么如何在已知玩家当前坐标与目的坐标的情况下，求得玩家应该朝向哪呢？

 

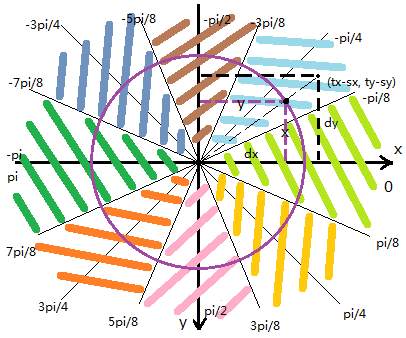
我们首先要将我玩家至于上图直角坐标系的(0,0)坐标处，根据几何平移变换，假设玩家坐标为sx,sy，目的坐标为tx,ty，那么当玩家平移至(0,0)处时，目的坐标则为(tx-sx, ty-sy)，我们简写为(dx, dy)，如图：

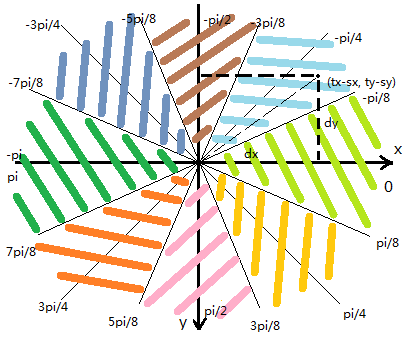
我们把原点与目的点连上，则形成了一个直角三角形。这时应该可以恍然大悟了，我们现在已知dy和dx，即已知tan的值。那么我们就可以根据某个目标点求tan，根据其值来了解他们落在上面哪个颜色之中。

 

在高中，我们还需要查表才知道某个角度的tan，现在我们有calc(计算器)，则可以直接求出上面这些关键角度的tan值，如下：

tan 0 = 0

tan pi/8 = 0.4142

tan pi/4 = 1

tan 3pi/8 = 2.4142

tan pi/2 = 无穷

tan 5pi/8 = -2.4142

tan 3pi/4 = -1

tan 7pi/8 = -0.4142

tan pi = 0

并且根据sin(a) = -sin(-a)和cos(a) = cos(-a)和tan(a) = sin(a) / cos(a)，我们得知tan(a) = -tan(-a)。

所以在上面的表的相对的负弧度的值取相反数即可。

 

通过分析上面的值，可以发现一个有意思的事——同一个tan值对应两个角度。这两个角度关于原点对称。这虽然使问题稍微麻烦了点，但也不难解决，只需要在求得tan之后，再比较dx是大于0还是小于0，就可以最终确定方向了。

 

总结一些这些值，我们将它们按域划分，如图：

因此，方向计算完成，c++实现代码如下：

int dx = TargetX - MapX; int dy = TargetY - MapY; double tg; if (dx == 0) { if (dy > 0) { Direction = 0; } else { Direction = 4; } } else { tg = (double)dy / dx; if (tg <= -2.4142) { Direction = dx > 0 ? 4 : 0; } else if (tg > -2.4142 && tg < -0.4142) { Direction = dx > 0 ? 5 : 1; } else if (tg >= -0.4142 && tg <= 0.4142) { Direction = dx > 0 ? 6 : 2; } else if (tg > 0.4142 && tg <2.4142) { Direction = dx > 0 ? 7 : 3; } else // tg >= 2.4142 { Direction = dx > 0 ? 0 : 4; } }

 

2. 优化移动速度

因为玩家的移动能力是一定的，为RunSpeed，那么反应在刚才的坐标变换图中可以画出在任意方向下的移动能力就是个圆，如下图：

由此可知该圆的半径为RunSpeed，我们要求出图上的x和y，这个x和y就是玩家在本帧应当移动的距离，而不是第一篇文章我们写死的RunSpeed本身。求x和y的问题也可以转换成一个三角形问题，如下图：

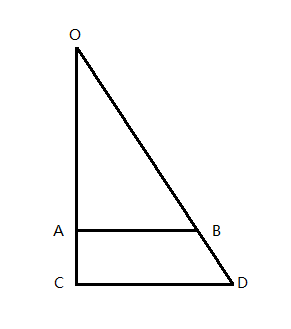
转换成几何问题的说法就是：已知OC、CD、OB，求OA、AB。

我们可以使用毕达哥拉斯定理求出OD。

然后根据某定理(实在忘了名称了)，可知OA:OC = OB:OD = AB:CD，可以求出OA和AB。

c++代码如下：

int x, y; double alpha = sqrt((double)dx * dx + dy * dy) / RunSpeed; x = dx / alpha; y = dy / alpha; if (abs(TargetX - (MapX + x)) < abs(x)) { MapX = TargetX; } else { MapX += x; } if (abs(TargetY - (MapY + y)) < abs(y)) { MapY = TargetY; } else { MapY += y; }

 

到此对玩家移动和方向的优化就完成了。

 

项目代码下载地址：>>点击进入下载页<<