不记得当初是怎么学概率论和数理统计的了。最近总是遇到一个小问题,想不通为什么样本方差的无偏估计量是要除以N-1的。
上Wiki找了一下,
Estimating variance
Suppose X1, ..., Xn are independent and identically distributed random variables with expectation μ and variance σ? Let
be the "sample average", and let
be a "sample variance". Then S?is a "biased estimator" of σ?because
Note that when a transformation is applied to an unbiased estimator, the result is not necessarily itself an unbiased estimate of its corresponding population statistic. That is, for a non-linear functionf and an unbiased estimator U of a parameter p, f(U) is usually not an unbiased estimator of f(p). For example the square root of the unbiased estimator of the population variance is not an unbiased estimator of the population standard deviation.
Bias is not the only consideration when choosing a statistic, however. Bias refers to the central tendency of the sampling distribution of a statistic, but the variance of the sampling distribution can also be an important consideration. Specifically, statistics with smaller sampling variances will yield greater statistical power. For example, while S?above is more biased than the traditional sample calculation
S?has a lower estimation variability than S?sub>sample because the denominator dividing the sum of squares is larger in the calculation of S? resulting in a smaller scale of final values, and therefore lower estimation variability, than that of S?sub>sample. Practically, this demonstrates that for some applications (where the amount of bias can be equated between groups/conditions) it is possible that a biased estimator can prove to be a more powerful, and therefore useful, statistic.
自由度(degree of freedom, df)是指当以样本的统计量来估计总体的参数时,样本中独立或能自由变化的数据的个数称为该统计量的自由度。
例如,在估计总体的平均数时,样本中的n个数全部加起来,其中任何一个数都和其他数据相独立,从其中抽出任何一个数都不影响其他数据(这也是随机抽样所要求的)。因此一组数据中每一个数据都是独立的,所以自由度就是估计总体参数时独立数据的数目,而平均数是根据n个独立数据来估计的,因此自由度为n。
但是为什么用样本估计总体的方差时,方差的自由度就是(n-1)?
s2= å(X-m)2/n
从此公式我们可以看出总体的方差是由各数据与总体平均数的差值求出来的,因此必须将m固定后才可以求总体的方差。因此,由于m被固定,它就不能独立自由变化,也就是方差受到总体平均数的限制,少了一个自由变化的机会,因此要从n里减掉一个。
假设一个样本有两个数值,X1=10,X2=20,我们现在要用这个样本估计总体的方差,则样本的平均数是:
Xm=å X/n=(10+20)/2=15
现在假设我们已知Xm=15,X1=10,根据公式Xm=å X/n,则有:
X2=2Xm-X1=2×15-10=20
由此我们可以知道在有两个数据样本中,当平均数的值和其中一个数据的值已知时,另一个数据的值就不能自由变化了,因此这个样本的自由度就减少一个,变成了(n-1)。依此类推:在一组数据中,当其平均数和前面的数据都已知时,最后一个数据就被固定而不能独立变化了,因此这个样本能够独立自由变化的数目就是(n-1)个.








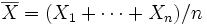
















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








