梯度下降算法学习笔记
内容来自于斯坦福大学《机器学习与数据挖掘公开课》。
介于算法中用到了许多线性代数的知识。所以我感觉有必要先对线性代数的基础知识做一个回顾和梳理。
1基础概念和记号
线性代数对于线性方程组可以提供一种简便的表达和操作方式,例如对于如下的方程组:
4x1-5x2=13
-2x1+3x2=-9
可以简单的表示成下面的方式:
X也是一个矩阵,为(x1,x2)T,当然你可以看成一个列向量。
1.1基本记号
用A ∈表示一个矩阵A,有m行,n列,并且每一个矩阵元素都是实数。
用x ∈ , 表示一个n维向量. 通常是一个列向量. 如果要表示一个行向量的话,通常是以列向量的转置(后面加T)来表示。
1.2向量的内积和外积
根据课内的定义,如果形式如xT y,或者yT x,则表示为内积,结果为一个实数,表示的是:,如果形式为xyT,则表示的为外积:
。
1.3矩阵-向量的乘法
给定一个矩阵A ∈ Rm×n,以及一个向量x ∈ Rn,他们乘积为一个向量y = Ax ∈ Rm。也即如下的表示:
如果A为行表示的矩阵(即表示为),则y的表示为:
相对的,如果A为列表示的矩阵,则y的表示为:
即:y看成A的列的线性组合,每一列都乘以一个系数并相加,系数由x得到。
同理,
yT=xT*A表示为:
yT是A的行的线性组合,每一行都乘以一个系数并相加,系数由x得到。
1.4矩阵-矩阵的乘法
同样有两种表示方式:
第一种:A表示为行,B表示为列
第二种,A表示为列,B表示为行:
本质上是一样的,只是表示方式不同罢了。
1.5矩阵的梯度运算(这是老师自定义的)
定义函数f,是从m x n矩阵到实数的一个映射,那么对于f在A上的梯度的定义如下:
这里我的理解是,f(A)=关于A中的元素的表达式,是一个实数,然后所谓的对于A的梯度即是和A同样规模的矩阵,矩阵中的每一个元素就是f(A)针对原来的元素的求导。
1.6其他概念
因为篇幅原因,所以不在这里继续赘述,其他需要的概念还有单位矩阵、对角线矩阵、矩阵转置、对称矩阵(AT=A)、反对称矩阵(A=-AT)、矩阵的迹、向量的模、线性无关、矩阵的秩、满秩矩阵、矩阵的逆(当且仅当矩阵满秩时可逆)、正交矩阵、矩阵的列空间(值域)、行列式、特征向量与特征值……
2用到的公式
在课程中用到了许多公式,罗列一下。嗯,部分公式的证明很简单,部分难的证明我也不会,也懒得去细想了,毕竟感觉上数学对于我来说更像是工具吧。
转置相关:
• (AT)T = A
• (AB)T = BT AT
• (A + B)T = AT + BT
迹相关:
• For A ∈ Rn×n, trA = trAT .
• For A, B ∈ Rn×n, tr(A + B) =trA + trB.
• For A ∈ Rn×n, t ∈ R, tr(tA) = t trA.
• For A, B such that AB issquare, trAB = trBA.
• For A, B, C such that ABC issquare, trABC = trBCA = trCAB。 当乘法变多时也一样,就是每次从末尾取一个矩阵放到前面去,这样的矩阵乘法所得矩阵的迹是一致的。
秩相关
• For A ∈ Rm×n,rank(A) ≤ min(m, n). If rank(A) = min(m, n), 则A称为满秩
• For A ∈ Rm×n,rank(A) = rank(AT).
• For A ∈ Rm×n, B ∈ Rn×p,rank(AB) ≤ min(rank(A), rank(B)).
• For A, B ∈ Rm×n,rank(A + B) ≤ rank(A) +rank(B).
逆相关:
• (A−1)−1 = A
• If Ax = b, 左右都乘以A−1 得到 x = A−1b.
• (AB)−1 = B−1A−1
• (A−1)T = (AT)−1. F通常表示为A−T.
行列式相关:
• For A ∈ Rn×n, |A| = |AT |.
• For A, B ∈ Rn×n, |AB| = |A||B|.
• For A ∈ Rn×n, |A| = 0,表示矩阵A是奇异矩阵,不可逆矩阵
• For A ∈ Rn×n and A 可逆, |A|−1 = 1/|A|.
梯度相关:
• ∇x(f(x) + g(x)) = ∇xf(x) + ∇xg(x).
• For t ∈ R, ∇x(t f(x)) = t∇xf(x).
• ∇xbT x = b
• ∇xxT Ax = 2Ax (if A 对称)
• ∇2xxT Ax = 2A (if A 对称)
• ∇A|A| =(adj(A))T = |A|A−T . adj=adjoint
3梯度下降算法和正规方程组实例应用
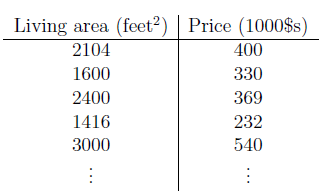
例子用的是上节课的房价的例子,有一组数据,有房子面积和房子价格,输入格式举例:
老师定义的变量如下:
m:训练样本的数目
x:输入的变量(输入的特征,在这个例子中为房子面积,后来又加了一个房子的卧室数目)
y :输出变量(目标变量,这个例子中就是房价)
(x,y):表示的是一个样本
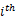
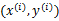
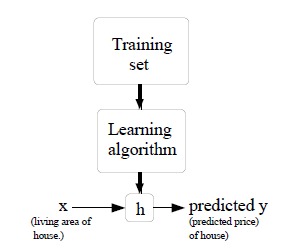
3.1监督学习概念
所谓的监督学习即为告诉算法每个样本的正确答案,学习后的算法对新的输入也能输入正确的答案 。监督指的是在训练样本答案的监督下,h即为监督学习函数。
此例中我们假设输出目标变量是输入变量的线性组合,也就是说,我们的假设是存下如下的h(x):
Theta表示是特征前面的参数(也称作特征权重)。也就是经过h(x)之后得到的就是预测的结果了。
如果假设x0=1,那么原来的h(x)就可以简单的表示为如下形式:
,其中n为特征数目,我们为了表达简便,把theta和x都写成向量的形式。下面就是如何求出θ(向量)使得h(x)尽可能接近实际结果的,至少在训练集内接近训练集中的正确答案。
我们定义一个花费函数(costfunction),针对每一组θ,计算出h(x)与实际值的差值。定义如下:
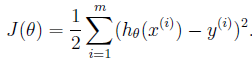
这也是用的最小二乘法的思想,但是之所以乘以1/2是为了简化后面的计算。针对训练集中的每一组数据。剩下的问题就是求得minJ(θ)时的θ取值,因为J(θ)是随着θ变化而变化,所以我们要求得minJ(θ)时的θ就是我们想要的θ(这个min也叫做最小花费函数),怎么样求出这组theta呢?采用的方法就是梯度下降算法和正规方程组。我们首先来看梯度下降算法。
3.2梯度下降算法
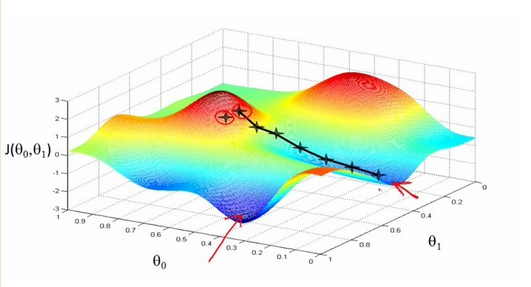
梯度下降算法是一种搜索算法,基本思想可以这样理解:我们从山上的某一点出发,找一个最陡的坡走一步(也就是找梯度方向),到达一个点之后,再找最陡的坡,再走一步,直到我们不断的这么走,走到最“低”点(最小花费函数收敛点)。
如上图所示,x,y表示的是theta0和theta1,z方向表示的是花费函数,很明显出发点不同,最后到达的收敛点可能不一样。当然如果是碗状的,那么收敛点就应该是一样的。
算法的theta更新表示如下:
对每一个theta(j),都先求J(θ)对theta(j)的偏导(梯度方向),然后减少α,然后将现在的theta(j)带入,求得新的theta(j)进行更新。其中α为步长,你可以理解为我们下山时走的步子的大小。步子太小了,收敛速度慢,步子太大了,可能会在收敛点附近来回摆动导致无法到达最低点。P.S.这个符号根据老师所说理解为程序中的赋值符号(=号),如果是=号,则理解为值是相等的(编程里面的==号)。
下面我们先理解下,假设现在训练集只有一组数据求关于theta(j)的偏导:
带入可以得到关于一组数据的theta(j)的表达式,不妨,这组数据就是第i组,则表示为:
然后我们将这个更新theta(j)的方法扩充到m个训练样本中,就可以得到下面的式子:
P.S.最外面的那个xj(i)的理解为:第i组数据中的第j个特征(feature)值。
3.2.1批量梯度下降算法(batch gxxxx dxxxx algorithm)
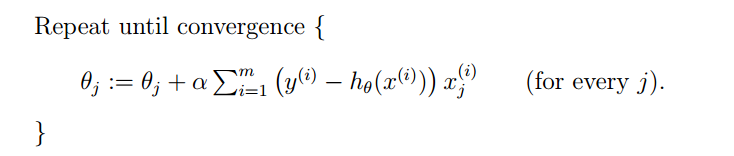
重复执行上面的这个更新步骤,直到收敛,就可以得到这组θ的值了。就是这个过程:
。
这个算法就是批量梯度下降算法,为什么叫批量梯度下降?因为注意到上式中每更新一个θj都需要计算所有的样本取值,所以当样本数目非常大的时候(例如上万条甚至数十万条的时候),这样的更新非常慢,找θ也非常慢,所以就有了另外一种改进的梯度下降算法。
3.2.2随机梯度下降算法/增量梯度下降算法
做一个小小的改进,用一个样本theta的更新。这种方法的好处是速度上肯定比批量梯度下降算法快,而且样本数据越多,体现应该就越明显。劣势是得到的收敛点的值和批量梯度算法比起来也许不是最优的值。
3.2.3梯度下降算法总结
不管是批量梯度算法还是随机梯度下降算法,他们的共同点有以下:
1.时间复杂度都是O(mn) (m为样本数目,n为特征值/影响因子数目)
2.都有梯度下降性质:接近收敛时,每次“步子”(指实际减去的数,而不是前面定义的α,α是手动设置参数,人为改变才会变)会越来越小。其原因是每次减去α乘以梯度,但是随着收敛的进行,梯度会越来越小,所以减去的值会。
3.判定收敛的方法都是如下两种:
1)两次迭代值改变量极小极小
2)J(θ)的值改变量极小极小
3.3正规方程组
写在前面:这种方法是另一种方法了,和梯度下降算法就没啥联系了!!!!!!
首先回顾下前面定义的矩阵梯度运算:
例如:
则:
定义一个矩阵,称作设计矩阵,表示的是所有的样本的输入:
因为前面得到的结论:(θT*x(i)和x(i)的转置*θ结果是一样),可以得到
可以写成如下的形式:
又因为对于任意向量,,所以可以得到:
运用下面介绍的一系列性质:
(5)是由(2)和(3)得到的,进行下面的推导
中间加tr不变的原因是因为是一个实数(看成1x1矩阵)加迹等于他本身。
将上式设为0,得到正规方程组
求解得到







 本文详细介绍了梯度下降算法的基本原理及其在机器学习中的应用,包括批量梯度下降与随机梯度下降的区别,并通过房价预测实例说明了算法的具体实现。
本文详细介绍了梯度下降算法的基本原理及其在机器学习中的应用,包括批量梯度下降与随机梯度下降的区别,并通过房价预测实例说明了算法的具体实现。
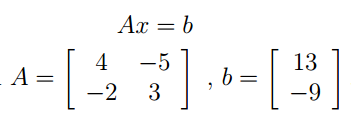
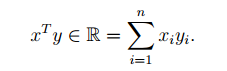
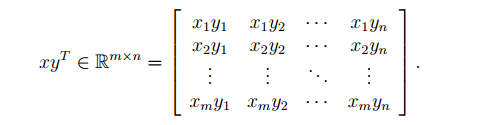
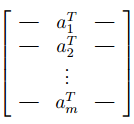
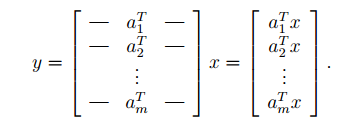
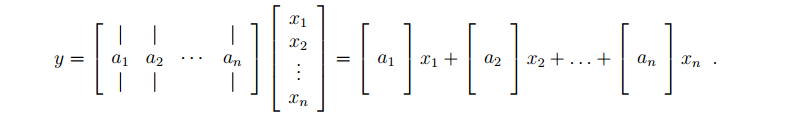
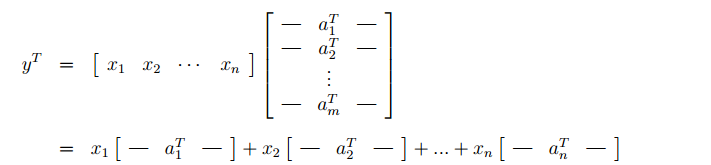
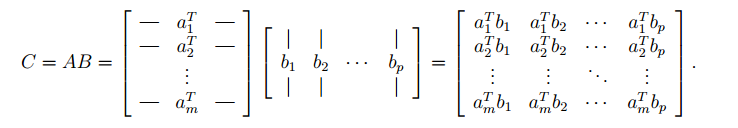
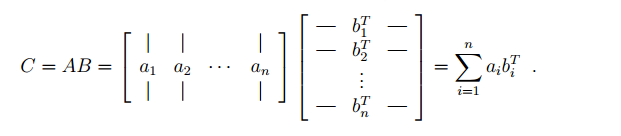
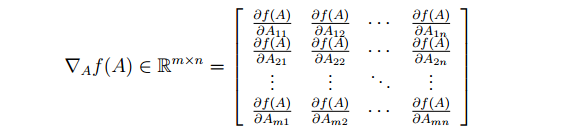
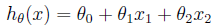
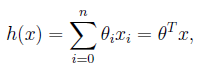
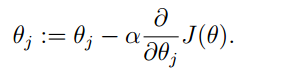
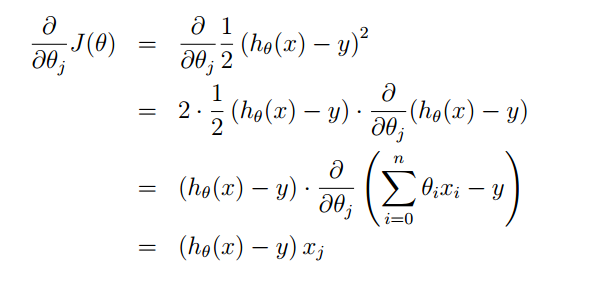
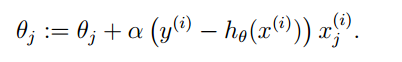
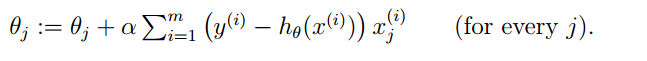
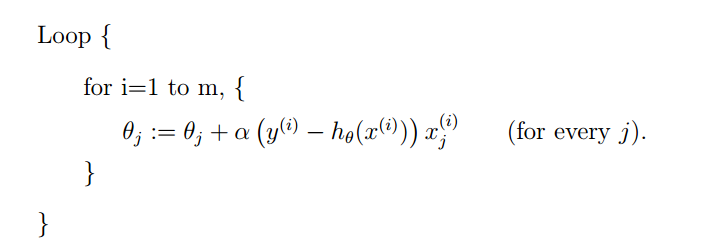
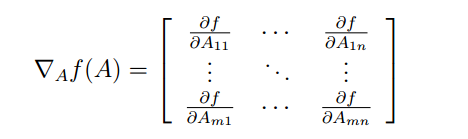
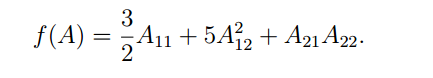
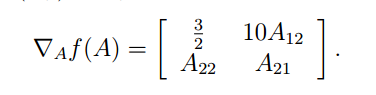
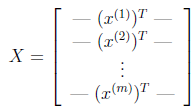
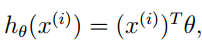
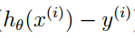
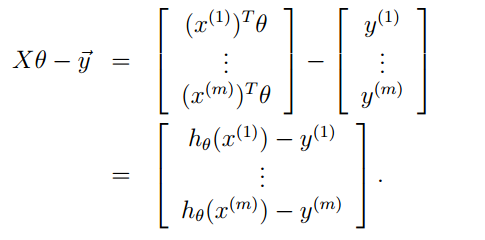
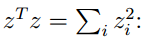
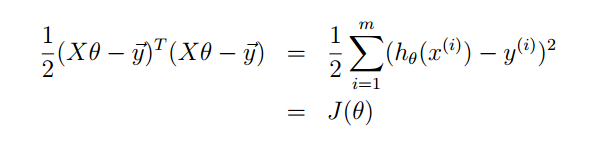
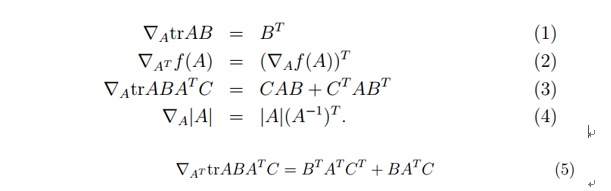
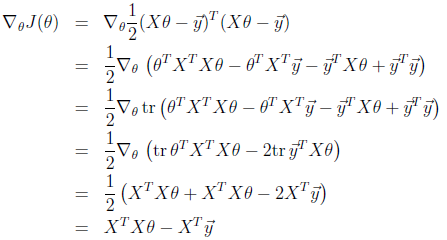
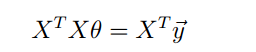
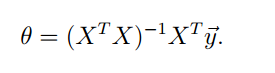
















 2248
2248










