大致题意:找出s的子串中字典序第k小的“半回文串”,给出半回文串定义是:对于任意i<=|s|/2 有s[i] = s[len-i+1]
数据量是5000
O(n^2)的算法可行
简单暴力的方法就是n^2 dp 出(i,j)的子串是不是半回文串,再把所有子串插入字典树,在dfs遍历出第k小的串
方法二,dp[i][j]统计出以i为始端到i~j的子串是回文串的总数,再把所有子串插入字典树,然后二分出答案子串。
方法一:
#include <iostream>
#include <cstring>
#include <cmath>
#include <queue>
#include <stack>
#include <list>
#include <map>
#include <set>
#include <sstream>
#include <string>
#include <vector>
#include <cstdio>
#include <ctime>
#include <bitset>
#include <algorithm>
#define SZ(x) ((int)(x).size())
#define ALL(v) (v).begin(), (v).end()
#define foreach(i, v) for (__typeof((v).begin()) i = (v).begin(); i != (v).end(); ++ i)
#define REP(i,n) for ( int i=1; i<=int(n); i++ )
using namespace std;
typedef long long ll;
const int N = 5000+5;
int dp[N][N];
char s[N];
int k;
int n;
struct node
{
node *son[2];
int cnt;
node()
{
memset(son,0,sizeof(son));
cnt = 0;
}
}trie[N*N];
int SZ = 0;
node *root,*cur;
node *createnode()
{
return &trie[SZ++];
}
void Insert(int p)
{
cur = root;
for(int i = p;i <= n;i++)
{
int val = s[i]-'a';
if(cur->son[val] == NULL) cur->son[val] = createnode();
cur = cur->son[val];
cur->cnt += dp[p][i];
}
}
int getsum(node *cur)
{
int sum = 0;
if(cur->son[0]) sum += getsum(cur->son[0]);
if(cur->son[1]) sum += getsum(cur->son[1]);
cur->cnt += sum;
return cur->cnt;
}
vector<char>ans;
bool dfs(node *cur,int &k)
{
if( k <= 0) return true;
if(cur->son[0])
{
ans.push_back('a');
if(cur->son[0]->cnt) k -= cur->son[0]->cnt;
if(dfs(cur->son[0],k)) return true;
ans.pop_back();
}
if(cur->son[1])
{
ans.push_back('b');
if(cur->son[1]->cnt)k -= cur->son[1]->cnt;
if(dfs(cur->son[1],k)) return true;
ans.pop_back();
}
return false;
}
int main()
{
scanf("%s%d",s+1,&k);
n = strlen(s+1);
for(int i =0;i <= n+2;i++)
for(int j = i;j >= 0;j--)
dp[i][j] = 1;
for(int len = 2;len <= n;len++)
for(int l = 1;l+len-1 <= n;l++)
{
int r = l+len-1;
dp[l][r] = (s[l] == s[r] && dp[l+2][r-2]);
}
root = createnode();
REP(i,n)Insert(i);
dfs(root,k);
foreach(i,ans) putchar(*i);
}
方法二:
//GNU C++ Accepted 374 ms 392200 KB
#include <iostream>
#include <cstring>
#include <cmath>
#include <queue>
#include <stack>
#include <list>
#include <map>
#include <set>
#include <sstream>
#include <string>
#include <vector>
#include <cstdio>
#include <ctime>
#include <bitset>
#include <algorithm>
#define SZ(x) ((int)(x).size())
#define ALL(v) (v).begin(), (v).end()
#define foreach(i, v) for (__typeof((v).begin()) i = (v).begin(); i != (v).end(); ++ i)
#define REP(i,n) for ( int i=1; i<=int(n); i++ )
using namespace std;
typedef long long ll;
const int N = 5000+5;
int dp[N][N];
char s[N];
int k;
int n;
struct node
{
node *son[2];
int cnt;
node()
{
memset(son,0,sizeof(son));
cnt = 0;
}
}trie[N*N];
int SZ = 0;
node *root,*cur;
node *createnode()
{
return &trie[SZ++];
}
void Insert(int p)
{
cur = root;
for(int i = p;i <= n;i++)
{
int val = s[i]-'a';
if(cur->son[val] == NULL) cur->son[val] = createnode();
cur = cur->son[val];
if(i != p)cur->cnt += dp[p][n]-dp[p][i-1];
else cur->cnt += dp[p][n];
}
}
void query(node*cur,int k) //二分过程
{
if(k <= 0) return ;
if(cur->son[0] && cur->son[0]->cnt >= k)
{
int cnt = cur->son[0]->cnt;
cur = cur->son[0];
if(cur->son[0]) cnt -= cur->son[0]->cnt;
if(cur->son[1]) cnt -= cur->son[1]->cnt;
putchar('a');
query(cur,k-cnt);
}
else if(cur->son[1])
{
if(cur->son[0]) k -= cur->son[0]->cnt;
int cnt = cur->son[1]->cnt;
cur = cur->son[1];
if(cur->son[0]) cnt -= cur->son[0]->cnt;
if(cur->son[1]) cnt -= cur->son[1]->cnt;
putchar('b');
query(cur,k-cnt);
}
}
int main()
{
scanf("%s%d",s+1,&k);
n = strlen(s+1);
for(int i =0;i <= n+2;i++)
for(int j = i;j >= 0;j--)
dp[i][j] = 1;
for(int len = 2;len <= n;len++)
for(int l = 1;l+len-1 <= n;l++)
{
int r = l+len-1;
dp[l][r] = (s[l] == s[r] && dp[l+2][r-2]);
}
REP(i,n)
for(int j = i+1;j <= n;j++) dp[i][j] += dp[i][j-1];
root = createnode();
REP(i,n) Insert(i);
query(root,k);
}










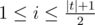 ) the following condition is held:
) the following condition is held: 












 1172
1172











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








