zzu数学 实验十一最速降线

zzu数学 实验十一最速降线

意大利科学家伽利略在1630年提出一个分析学的基本问题──“一个质点在重力作用下，从一个给定点到不在它垂直下方的另一点，如果不计摩擦力，问沿着什么曲线滑下所需时间最短”。他说这曲线是圆，可是这是一个错误的答案。 瑞士数学家约翰．伯努利在1696年再提出这个最速降线的问题（problem of brachistochrone），征求解答。次年已有多位数学家得到正确答案，其中包括牛顿、莱布尼兹、洛必达和伯努利家族的成员。

在一个斜面上，摆两条轨道，一条是直线，一条是曲线，起点高度以及终点高度都相同。两个质量、大小一样的小球同时从起点向下滑落，曲线的小球反而先到终点。这是由于曲线轨道上的小球先达到最高速度，所以先到达。然而，两点之间的直线只有一条，曲线却有无数条，那么，哪一条才是最快的呢？伽利略与1630年提出了这个问题，当时他认为这条线应该是一条弧线，可是后来人们发现这个答案是错误的。1696年，瑞士数学家约翰·伯努利解决了这个问题，他还拿这个问题向其他数学家提出了公开挑战。牛顿、莱布尼兹、洛比达以及雅克布·伯努利等解决了这个问题。这条最速降线就是一条摆线，也叫旋轮线。意大利科学家伽利略在1630年提出一个分析学的基本问题——“一个质点在重力作用下，从一个给定点到不在它垂直下方的另一点，如果不计摩擦力，问沿着什么曲线滑下所需时间最短。”。他说这曲线是圆，可是这是一个错误的答案。瑞士数学家约翰．伯努利在1696年再提出这个最速降线的问题（problem of brachistochrone），征求解答。次年已有多位数学家得到正确答案，其中包括牛顿、莱布尼兹、洛必达和伯努利家族的成员。这问题的正确答案是连接两个点上凹的唯一一段旋轮线。旋轮线与1673年荷兰科学家惠更斯讨论的摆线相同。因为钟表摆锤作一次完全摆动所用的时间相等，所以摆线（旋轮线）又称等时曲线。看一个稍微有点振奋人心的东西，Johann Bernoulli 对最速降线问题的beautiful解答：如果使分成的层数n无限地增加，即每层的厚度无限地变薄，则质点的运动便趋于空间A、B两点间质点运动的真实情况，此时折线也就无限增多，其形状就趋近我们所要求的曲线——最速降线．而折线的每一段趋向于曲线的切线，因而得出最速降线的一个重要性质：任意一点上切线和铅垂线所成的角度的正弦与该点落下的高度的平方根的比是常数．而具有这种性质的曲线就是摆线．所谓摆线，它是一个圆沿着一条直线滚动（无滑动）时，圆周上任意一点的轨迹。因此，最速降线就是摆线，只不过在最速降线问题中，这条摆线是上、下颠倒过来的罢了．

**Brachistochrone **

a = 10; h = 7; f[x_] := Sqrt[x]*h/Sqrt[a];
fig = Plot[-f[x], {x, 0, a}]

n = 16; fig1 = {};
Do[AppendTo[fig1, Line[{{a/n*i, 0}, {a/n*i, -f[a/n*i]}}]],
 {i, 1, n}]; Show[fig, Graphics[fig1]]

a=10;h=7;n=16;d=a/n;
g[y05_,y1_,y2_,y3_,y4_,y5_,y6_,y7_,y8_,y9_,y10_,y11_,y12_,y13_,y14_,y15_]:=
Sqrt[(0.5d)^2+y05^2]/Sqrt[y05]+Sqrt[(0.5d)^2+(y05-y1)^2]/(Sqrt[y05]+Sqrt[y1])+
Sqrt[d^2+(y1-y2)^2]/(Sqrt[y1]+Sqrt[y2])+
Sqrt[d^2+(y2-y3)^2]/(Sqrt[y2]+Sqrt[y3])+Sqrt[d^2+(y3-y4)^2]/(Sqrt[y3]+Sqrt[y4])+
Sqrt[d^2+(y4-y5)^2]/(Sqrt[y4]+Sqrt[y5])+Sqrt[d^2+(y5-y6)^2]/(Sqrt[y5]+Sqrt[y6])+
Sqrt[d^2+(y6-y7)^2]/(Sqrt[y6]+Sqrt[y7])+Sqrt[d^2+(y7-y8)^2]/(Sqrt[y7]+Sqrt[y8])+
Sqrt[d^2+(y8-y9)^2]/(Sqrt[y8]+Sqrt[y9])+Sqrt[d^2+(y9-y10)^2]/(Sqrt[y9]+Sqrt[y10])+
Sqrt[d^2+(y10-y11)^2]/(Sqrt[y10]+Sqrt[y11])+Sqrt[d^2+(y11-y12)^2]/(Sqrt[y11]+Sqrt[y12])+
Sqrt[d^2+(y12-y13)^2]/(Sqrt[y12]+Sqrt[y13])+Sqrt[d^2+(y13-y14)^2]/(Sqrt[y13]+Sqrt[y14])+
Sqrt[d^2+(y14-y15)^2]/(Sqrt[y14]+Sqrt[y15])+Sqrt[d^2+(y15-h)^2]/(Sqrt[y15]+Sqrt[h])

s=FindMinimum[g[y05,y1,y2,y3,y4,y5,y6,y7,y8,y9,y10,y11,y12,y13,y14,y15],{y05,0.5d},
{y1,d},{y2,2d},{y3,3d},{y4,4d},{y5,5d},{y6,6d},{y7,7d},{y8,8d},
{y9,9d},{y10,10d},{y11,11*d},{y12,12*d},{y13,13*d},{y14,14*d},{y15,15*d}]

points={0};
Do[AppendTo[points,s[[2,m,2]]],{m,1,16}];
AppendTo[points,h];
curve={{0,0},{0.5d,-points[[2]]}};
Do[AppendTo[curve,{(m-2)*d,-points[[m]]}],{m,3,18}];
pic1=ListPlot[curve,PlotJoined->True,AspectRatio->Automatic]

angle=FindRoot[h*t-h*Sin[t]+a*Cos[t]-a,{t,1.2Pi}];t0=angle[[1,2]];
r0=h/(1-Cos[t0]);
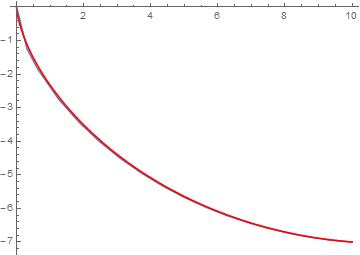
pic2=ParametricPlot[{r0(t0-Sin[t0]),-r0(1-Cos[t0])},{t0,0,t0},PlotStyle->{RGBColor[1,0,0]},AspectRatio->Automatic]

Show[pic1,pic2]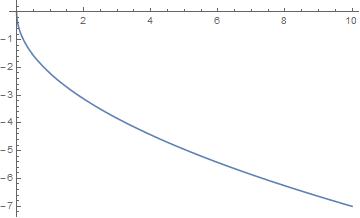

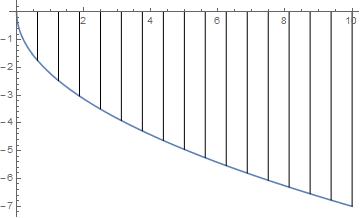
提供第二段代码

a = 10;
h = 5;
n = 16;
dx = a/n;
g = 9.8;
y =.;
yy = Table[y[k], {k, 1, n - 1}];
yy0 = Table[{y[k], h/a*k*dx}, {k, 1, n - 1}];
yy = AppendTo[yy, h];
yy = PrependTo[yy, 0];
Time[y_] := 
  dx*Sum[(1 + ((y[[k]] - y[[k - 1]])/dx)^2)^(0.5)/((2*g*
           y[[k]])^(0.5) + (2*g*y[[k - 1]])^(0.5))*2, {k, 2, n + 1}];
result = FindMinimum[Time[yy], yy0];
yy0 = Table[{k*dx, y[k]}, {k, 1, n - 1}];
xy = yy0 /. result[[2]];
xy = AppendTo[xy, {a, h}];
xy = PrependTo[xy, {0, 0}];
xy = Table[{xy[[k, 1]], -xy[[k, 2]]}, {k, 1, Length[xy]}];
fig1 = ListPlot[xy, Joined -> True]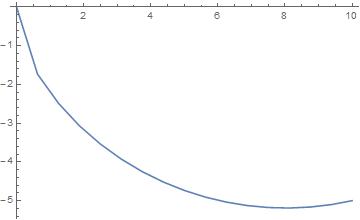

可以看到刚开始部分有个拐角。

求最速降线的问题其意义大大超过了问题的本身，因为很多物理过程，均可用求某些物理量的极值来解决。伯努利兄弟和其他科学家们从最速降线这个问题出发，创立了数学的一个分支——变分法。