解密SVM系列（二）：SVM的理论基础

上节我们探讨了关于拉格朗日乘子和KKT条件，这为后面SVM求解奠定基础，本节希望通俗的细说一下原理部分。

一个简单的二分类问题如下图：

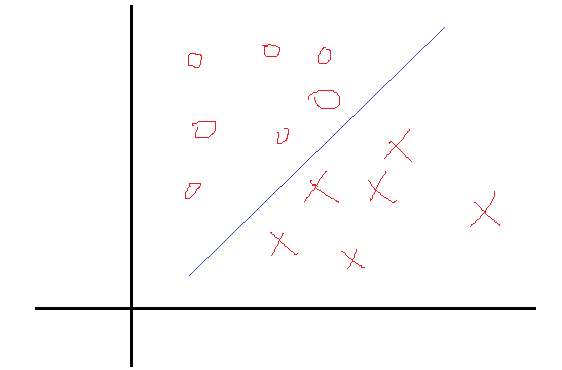
我们希望找到一个决策面使得两类分开，这个决策面一般表示就是$W^TX+b=0$,现在的问题是找到对应的W和b使得分割最好，知道logistic分类 机器学习之logistic回归与分类的可能知道，这里的问题和那里的一样，也是找权值。在那里，我们是根据每一个样本的输出值与目标值得误差不断的调整权值W和b来求得最终的解的。当然这种求解最优的方式只是其中的一种方式。那么SVM的求优方式是怎样的呢？

这里我们把问题反过来看，假设我们知道了结果，就是上面这样的分类线对应的权值W和b。那么我们会看到，在这两个类里面，是不是总能找到离这个线最近的点，向下面这样：

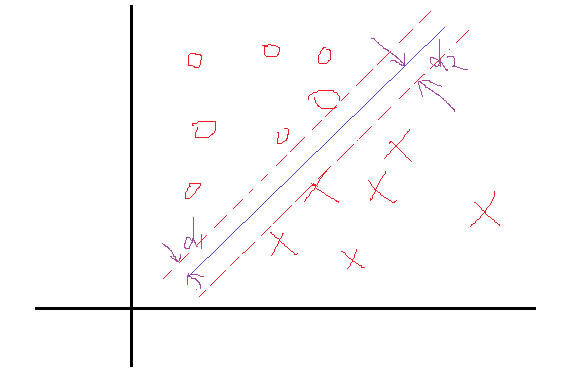
然后定义一下离这个线最近的点到这个分界面（线）的距离分别为d1,d2。那么SVM找最优权值的策略就是，先找到最边上的点，再找到这两个距离之和D，然后求解D的最大值，想想如果按照这个策略是不是可以实现最优分类，是的。好了还是假设找到了这样一个分界面$W^TX+b=0$,那么做离它最近的两类点且平行于分类面，如上面的虚线所示。好了再假设我们有这两个虚线，那么真实的分界面我们认为正好是这两个分界面的中间线，这样d1就等于d2了。因为真实的分界面为$W^TX+b=0$，那么就把两个虚线分别设置为$W^TX+b=1$和$W^TX+b=-1$可以看到虚线相对于真实面只是上下移动了1个单位距离，可能会说你怎么知道正好是一个距离？确实不知道，就假设上下是k个距离吧，那么假设上虚线现在为$W^TX+b=k$，两边同时除k可以吧，这样上虚线还是可以变成$W_1^TX+b_1=1$,同理下虚线也可以这样，然后他们的中线就是$W_1^TX+b_1=0$吧，可以看到从k到1，权值无非从w变化到w1,b变到b1,我在让w=w1,b=b1，不是又回到了起点吗，也就是说，这个中间无非是一个倍数关系。所以我们只需要先确定使得上下等于1的距离，再去找这一组权值，这一组权值会自动变化到一定倍数使得距离为1的。

好了再看看D=d1+d2怎么求吧，假设分界面$W^TX+b=0$，再假设X是两维的，那么分界面再细写出来就是：$w_1x_1+w_2x_2+b=0$。上分界线：$w_1x_1+w_2x_2+b=1$，这是什么，两条一次函数（y=kx+b）的曲线是不是，那么初中就学过两直线的距离吧，$d=\dfrac{|c_2-c_1|}{\sqrt{w_1^2+w_2^2}}=\dfrac{1}{||W||}$

这里W=(w1,w2)，是个向量，||W||为向量的距离，那么$||W||^2=W^TW$。下界面同理。这样$D=d1+d2=\dfrac{2}{||W||}=\dfrac{2}{\sqrt{W^TW}}等效\dfrac{2}{{W^TW}}$,要使D最大，就要使分母最小，这样优化问题就变为$min(\dfrac{1}{2}W^TW)$,乘一个系数0.5没影响，但是在后面却有用。

我们知道，如果一个一次函数分界面为$W^TX+b=0$，那么线上方的x可以使得$W^TX+b>0$,下方的x可以使得$W^TX+b<0$吧，那么对于上界面以上的点就有$W^TX+b>1$，下界面以下的点就有