http://blog.csdn.net/pipisorry/article/details/48579435
海量数据挖掘Mining Massive Datasets(MMDs) -Jure Leskovec courses学习笔记之链接分析:PageRank算法
链接分析与PageRank
{大图分析the Analysis of Large Graphs}
how the class fits together
图数据的例子
社交网络Social Networks(Facebook social graph\twitter)
社交媒体网络Social Media Networks(Connections between political blogs)
信息网Information Nets(Citation引用 networks between journals and Maps of science)
通信网Communication Nets(Internet)
技术网络Technological Networks(Seven Bridges of Königsberg, power grids, road networks water distribution networks)
理解这些网络的结构后就可以检测疾病暴发或者污染等等。
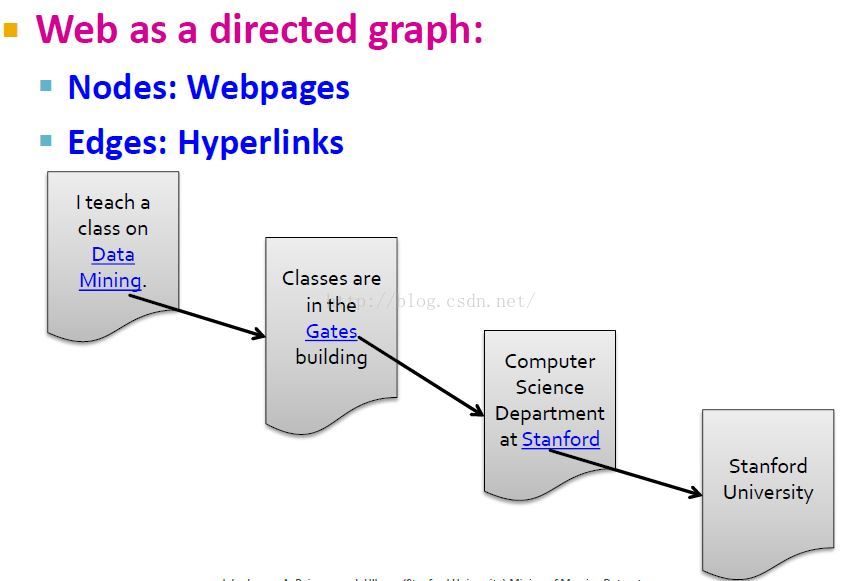
Web有向图
怎么去组织Web
1996年,yahoo的思想是将所有web页面手动分类到类别集合里。 the big question on the web is which web pages on the web should we trust?
Web搜索的2大挑战
链接分析算法:图节点重要性排序
计算图中节点的重要性:有很多链接的节点会有很高的重要性。
计算节点重要性的算法
不同于pagerank, Hubs and Authorities的思想是我们有两种类型的web页面,在web图中有称作hubs的web页面,也有称作authorities的页面。
皮皮Blog
流式公式The Flow Formulation
{PageRank的第一个数学公式,是标量化的公式而不是向量化的}
Idea: Links as votes
页面在web图中的引用和它获得的链接数目一样重要。the page quote on noting a graph is as important as the number of links it gets.
关于idea的两个问题
1. In-coming links? Out-going links?
in-links在某种程度上比out-links更难造假,你可以在自己的页面中加入很多外部链接,但是其它链接到你的页面就不一定了。
2. 所有的in-links是对等的吗?
来自重要页面的链接权重更大。 For example a link from a given web page maybe from stanford.edu is more important than a link from some other web page that only receives very few in-links.
这个思想就是页面的重要性在某种程度上取决于指向它的其它页面的重要性。
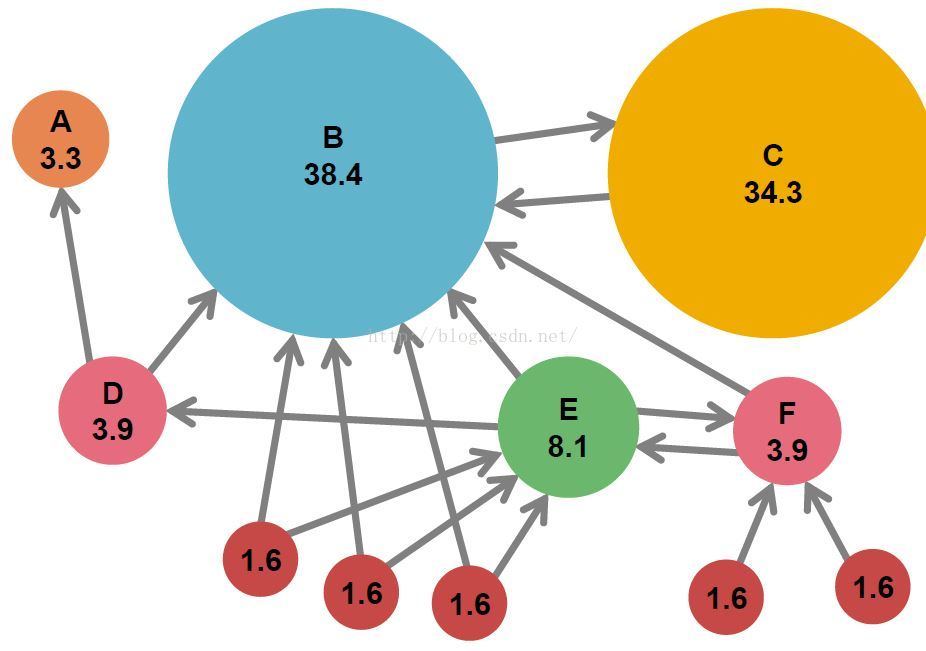
PageRank分数的一个例子
图中,节点大小代表pagerank分数score,并且规格化分数和为100。
节点C有相对较高的pagerank分数,即使它仅收到一个incoming link,但是它是由相当重要的一个节点B指向C的。
PageRank流模型The Flow Model
简单的递归公式
每个节点如节点j,从in-links中收集votes,并将自己的votes均分传播给out-links。思想就是pagerank分数在网络上流动,这就是the flow formulation of a flow model of PageRank.
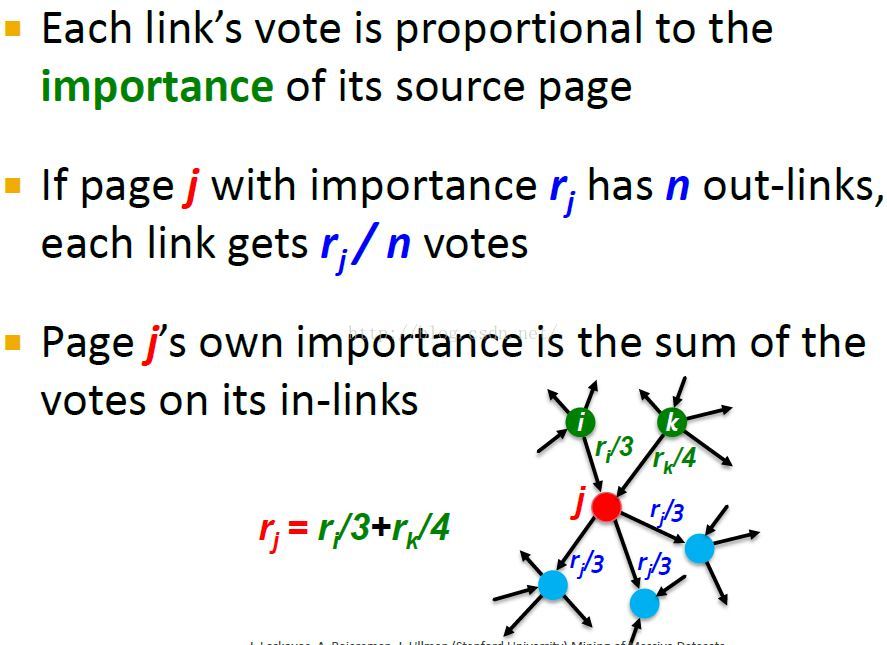
根据Graph建立流式等式
important score rank:给每个节点j赋予一个重要性分数R。节点j的重要性就是所有指向它的节点i的重要性除以那个节点的出度的和。(见图中公式)
求解流等式
三个变量三个等式的方程有无穷多个解,these solutions will have in common is that They will be equivalent up to the scaling factor(缩放因子).
加上一个归一化条件说可以使用Gaussian elimination(高斯消除法)可以求解以上公式,但是只能有效求解较小的网络图。
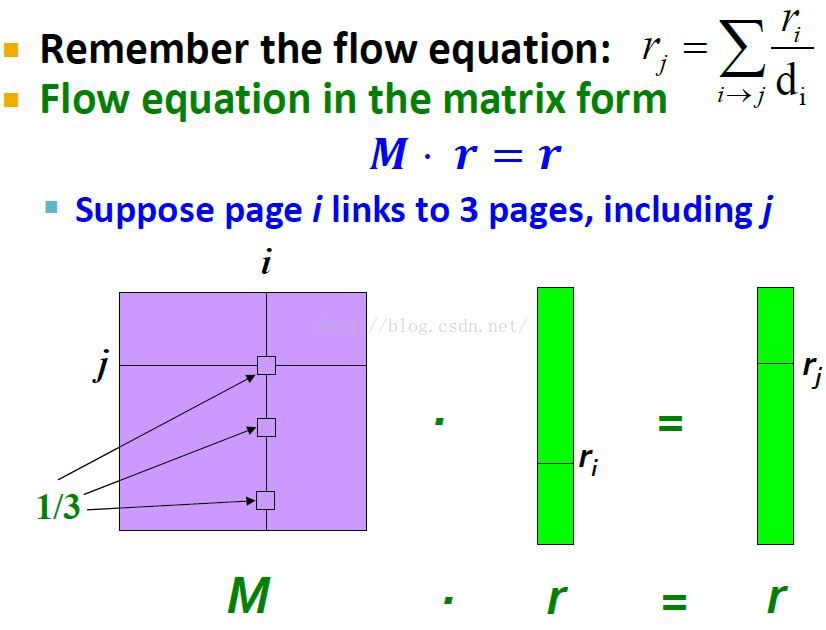
PageRank矩阵公式The Matrix Formulation
{pagerank的第二个数学公式,将上面的流式公式转换成矩阵公式,更简洁有效的求解图节点重要性}
图的随机邻接矩阵表示Stochastic Adjacency Matrix
矩阵M的每列i代表节点i不同的出度,列中的每个值分给不同出节点score的概率,和为1。
至于为什么要表示成列随机矩阵的形式(而不是行的),在下面的流式公式向量化中可以看出来。
节点page rank scores向量化
流式公式向量化:随机矩阵公式
这里可知M是固定值,我们要求的是r.
流式公式向量化的解释
简单来说就是右边向量中的entry条目rj(节点j的重要性)对应于左边矩阵M第j行(节点j的in-links,第j行向量中的每个值对应于1/di)与左边rank向量(rank向量中的每个值对应于ri)的乘积。
特征向量公式
建立随机矩阵公式的矩阵M的特征值和特征向量之间的联系,将随机矩阵公式r=M.r看成是求解特征向量的问题:
找到这种联系后,我们不再求解方程等式问题,而是寻找矩阵M的特征向量(主特征向量principal eigenvector:特征值为1对应的特征向量。)。
这样我们就只要求解M矩阵对应于特征值1的特征向量r,就求解出了web图中每个节点的重要性。
而求解这个特征向量的方法一般使用Power iteration.
小实例
Power iteration幂迭代
{求解web图节点重要性r,也就是求解随机矩阵公式r=M.r中矩阵M特征值1对应的特征向量r。这个幂迭代公式在r一定收敛的情况下才有效}
幂迭代方法
首先随机给r一个值,通过下图中的迭代公式计算出r的平稳结果,就计算出了r的近似值。
Note:
1. 范数Norm:
给定向量x=(x1,x2,...xn) L1范数:向量各个元素绝对值之和 L2范数:向量各个元素的平方求和然后求平方根,也叫欧式范数。 Lp范数:向量各个元素绝对值的p次方求和然后求1/p次方 L∞范数:向量各个元素求绝对值,最大那个元素的绝对值
2.epsilon的取值可以设为10^-6,程序中表示如epsilon=pow(e,-6)或者1.0e-6。
随机游走解释和平稳分布
{Random Walk Interpretation & The Stationary Distribution,解释pagerank分数score的意思,pagerank分数实际上等价于图的随机游走的概率分布。page rank scores are equivalent to a probability distribution of our random walker in a graph}

1. P(t)就是给定时间,所有图中节点的概率分布。每个节点上的概率值就是给定时间random walker在这个节点上的概率。
2. 不管random walker在给定节点上的概率是多少,现在random walker要选择一个从节点i出发,指向节点j的out-link。直白来说,就是将幂迭代方法中的r(t)看成t时刻,选择节点的概率分布。
3. pagerank分数对应于random surfer在web图上给定时间给定节点的无限次游走的概率。what page rank score corresponds to the probability that this random surfer,that infinitely long kind of walks the web graph at some given time t resides at the given node.The random walk interpretation of page rank, where we can think of a score or a rank of a given node to be the probability that the random walker is at that given node at some fixed time t.
存在和唯一性Existence and Uniqueness
随机游走random walks实际上叫做马尔科夫过程Markov processes或者first order Mark, order Markov processes。所以如果你了解马尔科夫过程的平稳分布,你就会知道平稳的条件以及为嘛这样迭代就会到达平稳分布状态。
平稳分布的条件:certain conditions On the structure of our matrix M:也就是非周期,状态连通。(lz的总结)
马氏链收敛定理
上面这个定理的一些解释:
谷歌公式The Google Formulation
{解决幂迭代公式不收敛问题,也就是web图节点重要性概率分布的存在性和唯一性问题。certain conditions that matrix M has to satisfy in order for the PageRank to exist and to be unique}
Note:其实下面的几个问题从上面lz关于markov收敛性中就可以轻松解释,spider trap和dead end本质是都是状态转移矩阵任意两个状态不是连通的,没有满足马氏链收敛定理。(不过两个节点的时候不能这么解释,如第1.1个例子)
PageRank向量化流式公式的三个问题
1. 公式是否收敛?
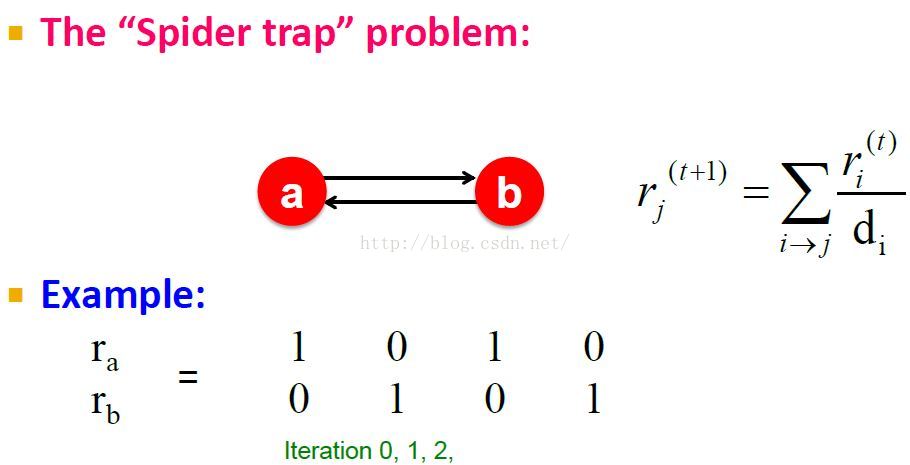
不收敛问题:The “Spider trap” problem,trap节点的概率权重总在增大。
在这个case中,m是一个spider trap,因为m有 self loop。这样当random walker到达这个节点后没有出路,陷入其中了,总是在m上,使其概率为1了。
2. 公式是否收敛到我们想要的结果?
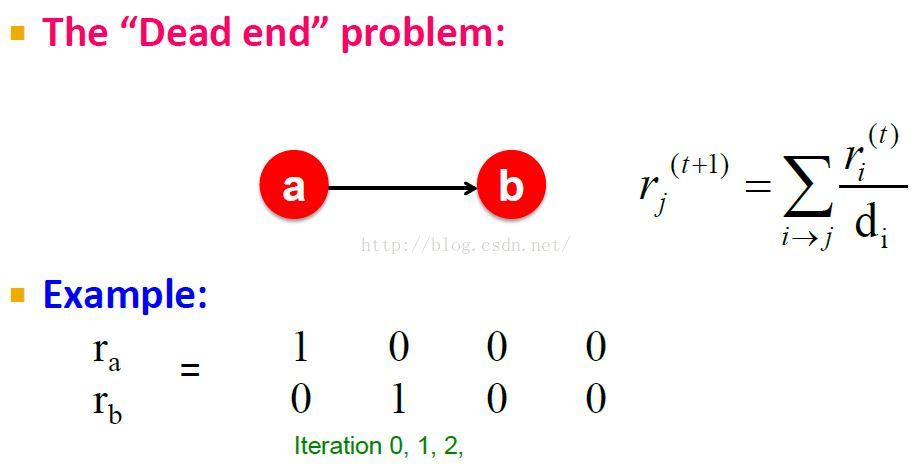
得到非想要的结果:The “Dead end” problem,死节点总是泄漏pagerank分数。
a, b不能将分数score传递给其它节点,这样分数就丢失了,最终收敛到0向量。
matrix m不再是随机的了,列和不再为1,而成了0向量。
3. Are results reasonable?
由前两个问题引出
前两个问题产生的原因
问题1:dead-ends就是没有outgoing links的网页,没有出度的节点,其节点重要性不能向下传播,就会泄漏遗失leak out。
问题2:网页的out-links形成一个小组。当random walker进入这个group中时会陷进去。at the end, those pages in that part of the graph will get very high weight, and every other page will get very low weight.
前两个问题的解决方案
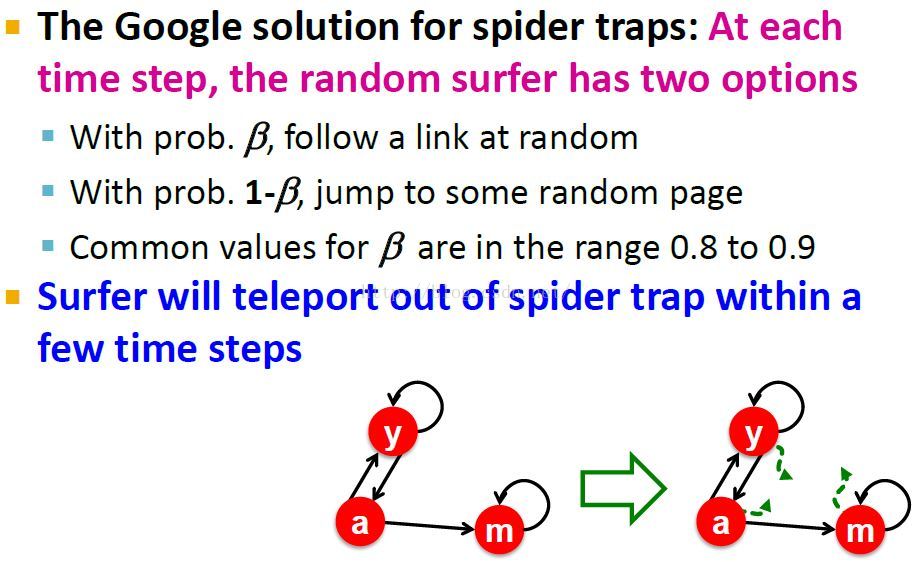
Spider Trap问题的解决
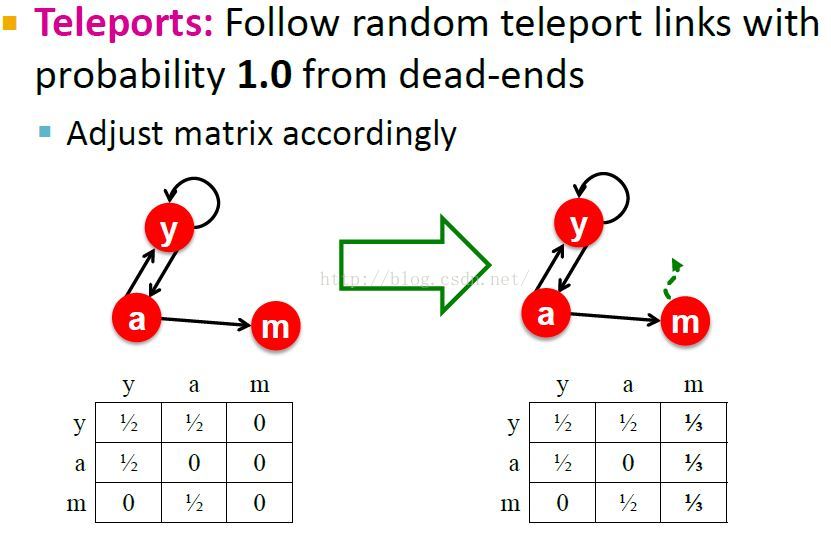
改变随机游走的方式:使用randomly teleport随机瞬移(远程传送),也就是为每个节点添加了一个小概率出度。
Dead End问题的解决
Always Teleport总是瞬移
也就是说,当我们到达一个节点m时,我们总会以随机均匀分布的概率teleport到其它地方。
瞬移(Teleport)能解决以上问题的原因
{使用马尔可夫链解释瞬移}
Markov Chain马尔可夫链
Note: Pij measures the probability that if we were at state i, how likely are we to transition to state j in a given time stamp.
马尔可夫链定理
Note: 也就是说状态转移矩阵P(也就是PageRank计算公式中的M矩阵)必须是随机的、不可约的、非周期的。而瞬移在某种程度上就是让M满足了这三个条件。actually adding random teleports gives us a in some sense stochastic transition matrix that has these properties.
Teleport是怎样使M具有随机性stochastic的
{dead end的解决?}
Note:
1. 一个矩阵是随机的就是说它的列和为1。
2. 注意这里的A和M是矩阵,而a和e是列向量。
3.Teleport通过将列和为0的列转换成非0列,从而使矩阵M是随机的。
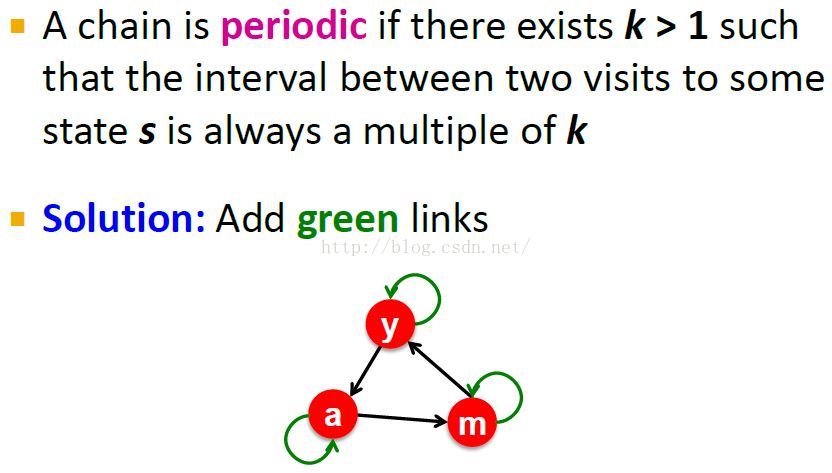
Teleport是怎样使M具有非周期性aperiodic的
Note:
1. 周期的:访问同一个状态(节点)的间隔总是某个k的倍数。
2. the random lock here is deterministic and every two steps we return back to the same node.
3. 加入Teleports(如图中的绿线)就打破了周期性。
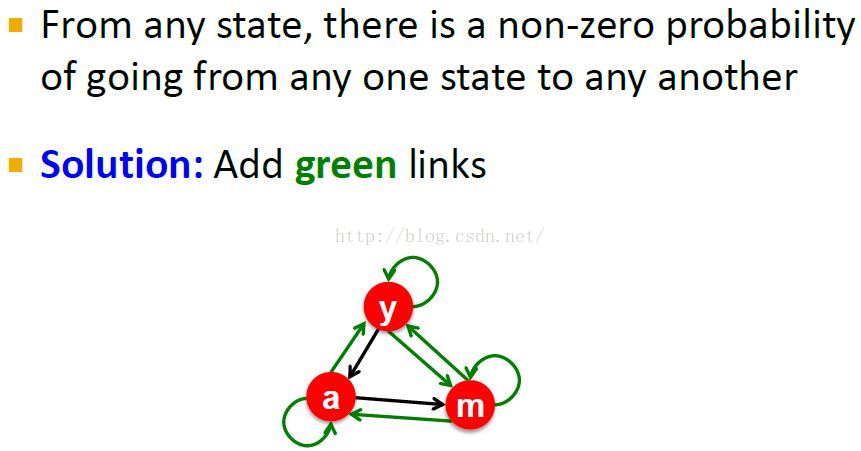
Teleport是怎样使M具有不可分性irreducible的
Note:
1. Irreducible also means that we can never get stuck in a given state.
2. we would make our given graph here irreducible is to add all these other possible links, which basically means we would add a random jumps.
回到Google的解决方案:随机跳转(Random Jump / Teleport)
{假设没有dead ends?}
Note:
1. PageRank equation的解释: Theimportance of node j is first.The sum of the importances of all the nodes ithat point to it.Then we divide that by the outdegree of i as the probabilitythat the random walker actually traverse the link towards j.And, this onlyhappens with probability beta because the random walker,when they are at nodeI,has to decide to actually follow a link, and this happens with probabilitybeta.And then of course, how likely is the random walker to visit node J?Withprobability one minus beta the random walker decides to jump.And if the randomwalker decides to jump then it will land at a given node J with probability oneover N where N is the number of nodes in the network.
2. 式中前半部分是random walk*beta,后半部分是random jump*(1-beta)
其实上面的解决方案实质上不就是让状态转移矩阵任意两个状态之间都是连通(通过任意步可达)的吗?(回头看看lz的笔记:幂迭代部分Note中关于马氏链的收敛定理)
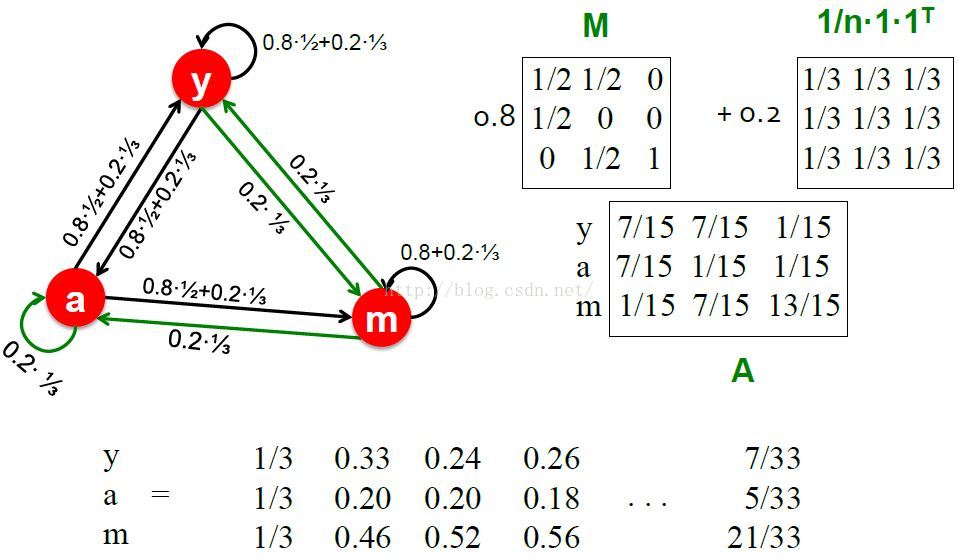
加入teleport后改进的Google Matrix
Note:
1. 一般将beta设置为0.85.Which basically means for every five steps you do a random jump.(0.85:0.15≈5:1)
2. 如果考虑dead end:
应该要在A中加入+这个吧,参考上面“Teleport是怎样使M具有随机性stochastic的”部分。
或者还是将beta设成一个矩阵,对应于M中列为0(dead end)的beta项设为0,这样random walker到达dead end时就总是random jump(teleport)了,参考上面“回到Google的解决方案:随机跳转(Random Jump / Teleport)”对应的图中绿色字体部分。
或者还是在每次计算新的r后会有score泄漏,导致r和不为1,这样我们每次计算完r后,将r renormalize,使其和为1,参考下面“Sparse Matrix Formulation稀疏矩阵公式”图中绿色字体部分部分。这个也就是真正采用的方法,其具体解决方案会在"PageRank完整算法"部分处理,并且会和spider trap一同合并处理,没讲到时都假定M中没有dead end。
Random Teleports实例
Note: matrix M is still stochastic, theonly problem is that node m is a spider trap.即使是这样,改进后的Google Matrix还是能很好的解决问题。
PageRank实际计算
{怎么计算图的pagerank分数,而甚至不用将其全部弄到内存中。how do we compute it for graphs that don't even fit into the main memory of a machine}
存储r需要2*4*10^9=8G; 存储A需要4*(10^9)^2=4000P太大了,不可能。
Matrix公式的等价公式
之前的公式
我们要从每页中抽取1-beta的概率用于重新分配,这样Matrix公式可以修改成下面等价的公式。
重新计算后等价的公式
其实没必要这么推导,直接将A = betaM+(1-beta)/n代入r = A.r中不就得到了吗。
这样修改Google公式后就不用再去求解矩阵A(A是一个很大的稠密矩阵)。而只用稀疏矩阵M,从而可以节省很多内存。
Sparse Matrix Formulation稀疏矩阵公式
这里先假设M没有dead end,具有dead end的M的处理将在下面完事算法给出。
PageRank完整算法
这个最终算法中我们同时考虑图中存在spider traps和dead ends。
考虑了dead end,也就是r的计算要在最后加入泄漏的score,1-S就是总的泄漏scores,再平均加到每个rj中。
特别要注意的是,泄漏的score也包含了(1-beta)/N部分。
如果不考虑泄漏的score,本来是要加(1-beta)/N的,但是考虑后(1-beta)/N隐含地加入到了泄漏的score中。
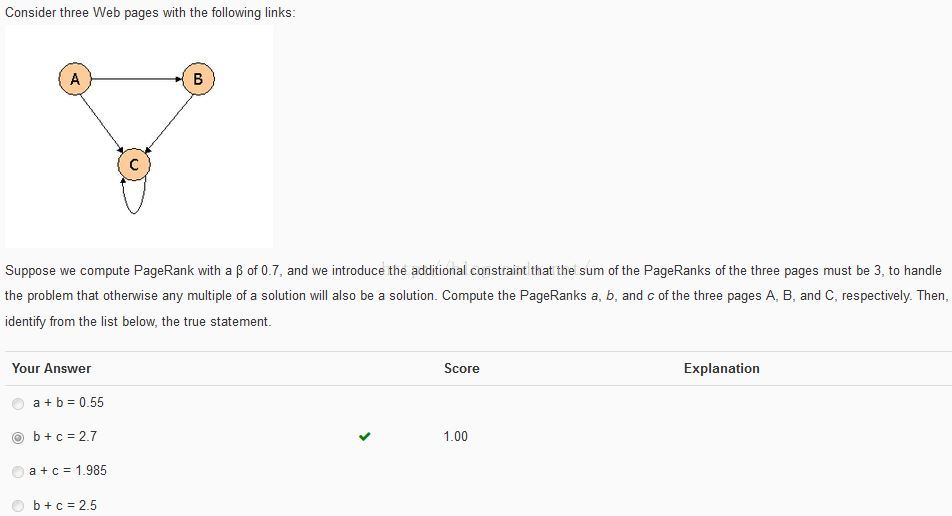
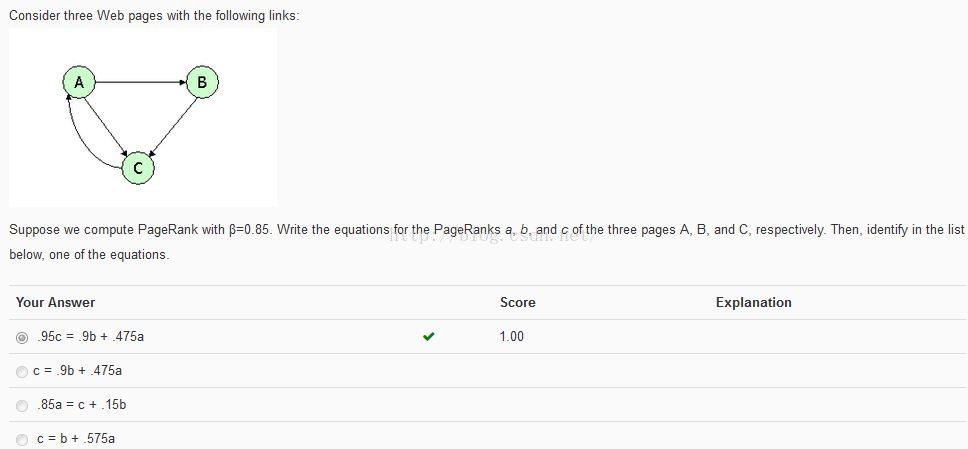
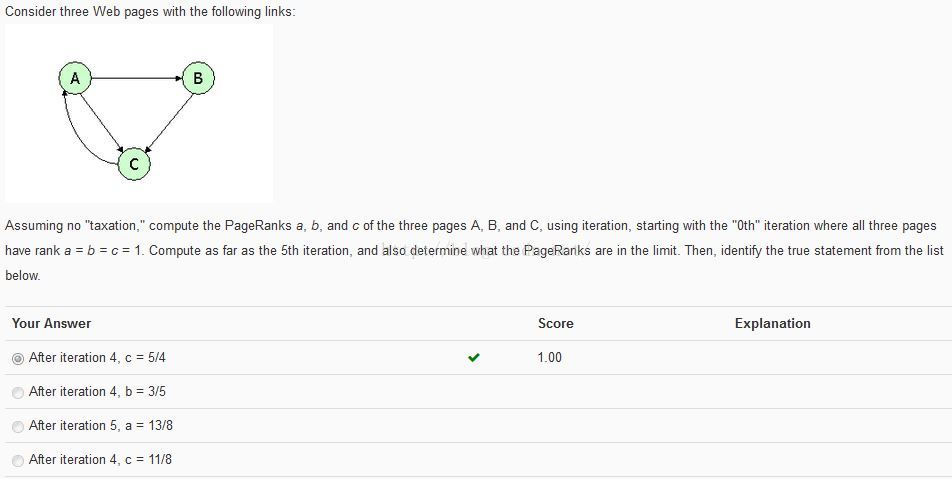
Feedback习题反馈 — Week 1 (Basic)
Note: 此题有一个小trick: 就是手算时你会发现a的值总是0.1*3,也就是说b+c = 1*3 - 0.3 = 2.7
python编程实现:
#!/usr/bin/env python # -*- coding: utf-8 -*- """ __title__ = '' __author__ = '皮' __mtime__ = '9/25/2015-025' __email__ = 'pipisorry@126.com' # code is far away from bugs with the god animal protecting I love animals. They taste delicious. ┏┓ ┏┓ ┏┛┻━━━┛┻┓ ┃ ☃ ┃ ┃ ┳┛ ┗┳ ┃ ┃ ┻ ┃ ┗━┓ ┏━┛ ┃ ┗━━━┓ ┃ 神兽保佑 ┣┓ ┃ 永无BUG! ┏┛ ┗┓┓┏━┳┓┏┛ ┃┫┫ ┃┫┫ ┗┻┛ ┗┻┛ """ from math import e import numpy as np def pageRank(M, r, beta, epsilon, flag=False): it_count = 0 N = r.size # print(N) while (True): it_count += 1 r_new = beta * np.dot(M, r) + (1 - beta) / N if flag and (it_count == 4 or it_count == 5): print('%s次迭代后:%s' % (it_count, r_new)) # print(sum(abs(r - r_new))) if sum(abs(r - r_new)) < epsilon: break r = r_new return r, it_count def question1(): M = np.array([[0, 0, 0], [0.5, 0, 0], [0.5, 1, 1]]) print(M) r = np.array([1, 1, 1]).T print(r) beta = 0.7 print('.' * 50) r, it_count = pageRank(M, r, beta=beta, epsilon=pow(e, -6)) print("%s\n%s次迭代" % (r * 3, it_count)) def question2(): M = np.array([[0, 0, 1], [0.5, 0, 0], [0.5, 1, 0]]) print(M) r = np.array([1 / 3, 1 / 3, 1 / 3]).T print(r) beta = 0.85 print('.' * 50) r, it_count = pageRank(M, r, beta=beta, epsilon=pow(e, -6)) print("%s\n%s次迭代" % (r, it_count)) a, b, c = r epsilon = pow(e, -6) if abs(0.95 * c - (0.9 * b + 0.475 * a)) < epsilon: print('True1') if abs(c - (0.9 * b + 0.475 * a)) < epsilon: print('True2') if abs(0.85 * a - (c + 0.15 * b)) < epsilon: print('True3') if abs(c - (b + 0.575 * a)) < epsilon: print('True4') def question3(): M = np.array([[0, 0, 1], [0.5, 0, 0], [0.5, 1, 0]]) print(M) r = np.array([1, 1, 1]).T print(r) beta = 1 print('.' * 50) r, it_count = pageRank(M, r, beta=beta, epsilon=pow(e, -6), flag=True) print("%s\n%s次迭代" % (r, it_count)) question1() print('*' * 50, '\n\n') question2() print('*' * 50, '\n\n') question3()from: http://blog.csdn.net/pipisorry/article/details/48579435
ref:深入浅出PageRank算法
高效的个性化PageRank算法:《Efficient Algorithms for Personalized PageRank》P Lofgren [Stanford University] (2015) 线性代数+蒙特卡罗 实现速度显著改善的(双向随机游走)个性化PageRank算法(可用于搜索/推荐场景)[https://github.com/plofgren/bidirectional-random-walk]














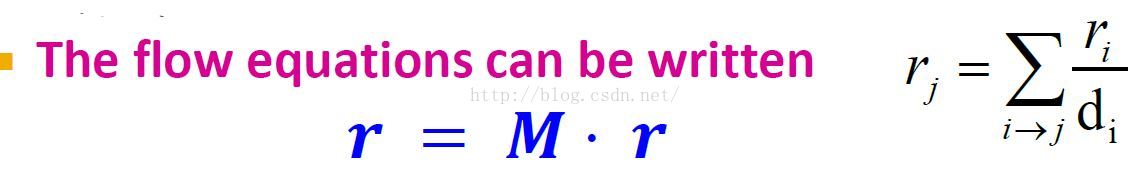







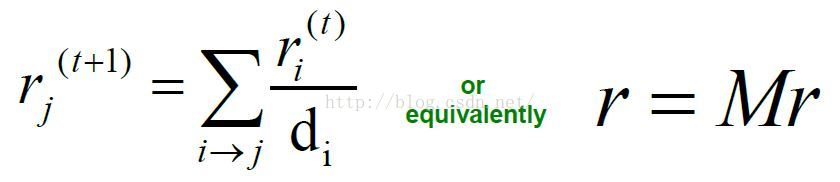



























 2562
2562

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








