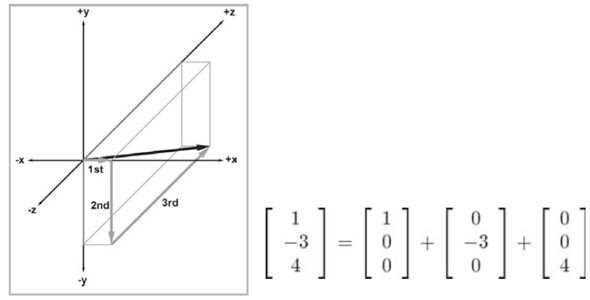
先通过向量来理解矩阵。向量[1, -3, 4]可以解释成如下的向量的加法
任意向量v都可以写成如下扩展形式
进一步写成:
右侧的单位就是x, y, z轴,记为nx, ny, nz。我们可以将其写成:
v=x*nx+y*ny+z*nz
如果我们用向量p,g,r重写nx, ny, nz意义不变:
v=xp+yg+zr
这里p,g,r就称为基向量,在这里它们是笛卡尔坐标轴。事实上,一个坐标系能用任意三个线性无关的向量作基向量来定义,[x,y,z]是向量v在以p,g,r为基向量的坐标系中的表示。以p,g,r为行定义一个3*3矩阵M,得到








 本文探讨了矩阵在几何中的意义,指出矩阵的行作为基向量可以表示坐标系的转换。通过矩阵乘法,向量在不同坐标系间的变换得以实现,包括旋转、缩放等效果。矩阵M将原坐标系下的向量a转换为新坐标系下的向量b,保持了相对位置的关系。总结来说,矩阵是描述坐标变换的重要工具。
本文探讨了矩阵在几何中的意义,指出矩阵的行作为基向量可以表示坐标系的转换。通过矩阵乘法,向量在不同坐标系间的变换得以实现,包括旋转、缩放等效果。矩阵M将原坐标系下的向量a转换为新坐标系下的向量b,保持了相对位置的关系。总结来说,矩阵是描述坐标变换的重要工具。
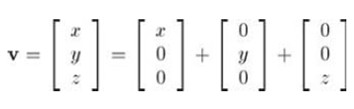
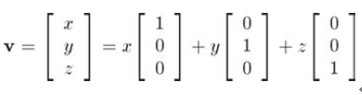
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 3471
3471

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








