角点:有两种比较普遍的定义
- 角点是两个边缘的交点
- 角点是邻域内具有两个主方向的特征点(这个主方向,其实我一直是迷糊,但是参考PCA,觉得其想说的是在在两个方向上灰度变化比较大,也就是此时的角点邻域内的点,不再是一个二维的点(x,y),而是一个三维的点(x,y,I)其中I是像素位置(x,y)对应的灰度值。当存在两个主方向时,也就意味着存在两个较大的特征值。)
角点检测的主要思路:
- 第一种基于图像边缘的方法,对应角点定义1,检测出边缘也便检测出角点。但是这种方法很依赖于图像边缘的检测结果,但是我们知道边缘检测是一个比较麻烦,复杂的问题。
- 第二种是基于图像灰度的方法,该方法主要通过计算点的曲率以及梯度来检测角点,这类方法中比较有代表性的有:Moravec,Forstner,Harris,SUSAN.
Harris角点检测:
下图可以很明了的说明Harris角点检测的原理:
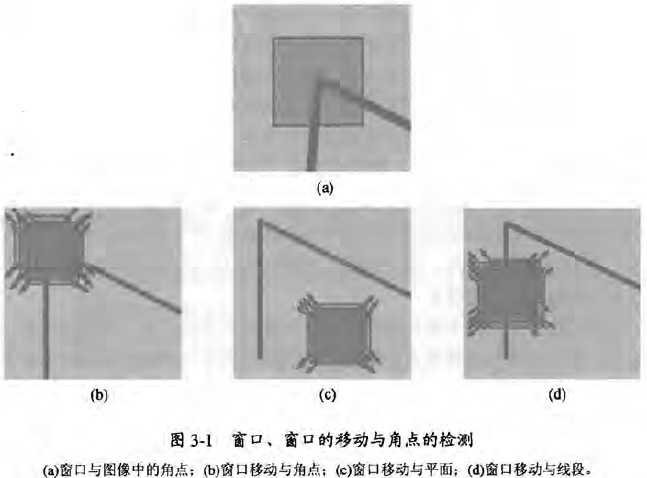
简单介绍就是,设置一个固定尺寸的小窗口,移动窗口。统计移动前后窗口内的像素变化情况,来进行角点的判断。写成数学表达式就是:
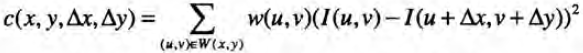
其中的权重因子w(u,v)可以是常数也可以是高斯加权函数:
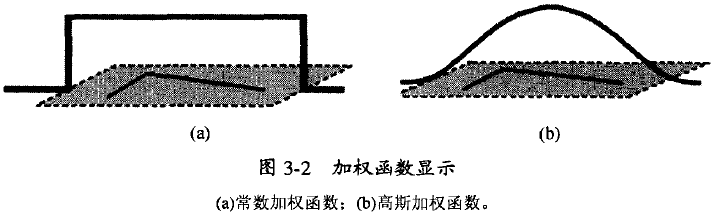
对上式进行泰勒级数的一阶展开,化简可以得到下式:
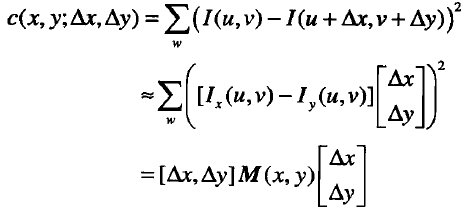
其中:
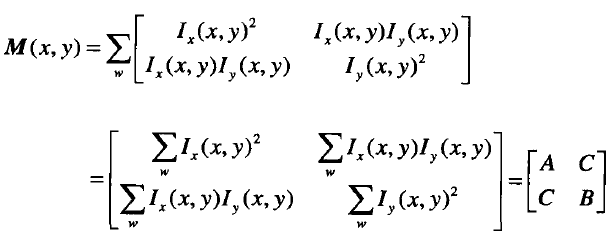
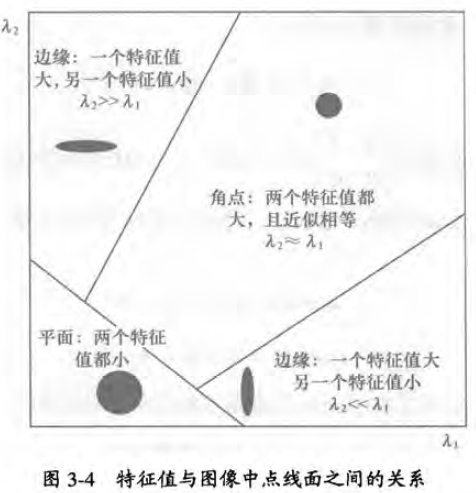
正如角点的第二种定义,角点是其邻域内的灰度在两个方向有较大的变化,对应存在两个较大的特征值;而边缘时邻域内的灰度在某一个方向有较大的变化,对应存在一个较大的特征值;平面就是在邻域内的灰度变化不大,存在两个较小的特征值;下图描述了特征值与检测结果的关系:
但是在求解矩阵M的特征值的时候,计算量比较大,比较耗时,因为我们一般不直接计算其特征。利用如下公式间接比较其特征的大小关系,进行角点判断:
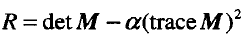
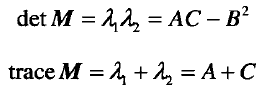
然后令λ1=λ,λ2=kλ1,其中(λ1>=λ2,故k<=1)
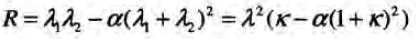
假设R>0,就有(高中数学中的对勾函数的极值问题,或者直接求导):
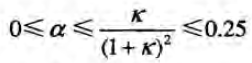
故调节α就可以设置k的数值范围:
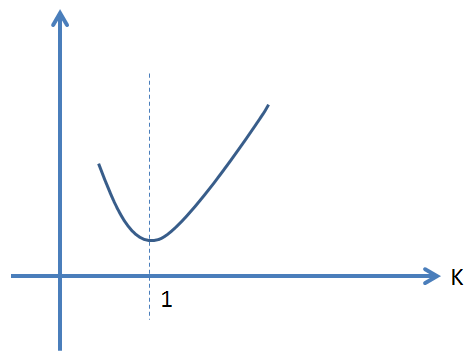
当α增大至0.25时,k就只能取1了;当α减小至0时,k的取值就是(0,1)了,也就是α值增大,k的取值区间减小,那么检测到的角点就变少,也就是检测灵敏性降低(但是更加准确);α值减小,k的取值区间增大,那么检测到的角点就变多,也就是检测灵敏性增加(但是会带来误检测)





















 1197
1197











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








