在人工神经网络(ANN)中,Softmax通常被用作输出层的激活函数。这不仅是因为它的效果好,而且因为它使得ANN的输出值更易于理解。同时,softmax配合log似然代价函数,其训练效果也要比采用二次代价函数的方式好。
1. softmax函数及其求导
softmax的函数公式如下:
其中,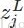
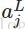
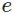
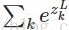
softmax函数最明显的特点在于:它把每个神经元的输入占当前层所有神经元输入之和的比值,当作该神经元的输出。这使得输出更容易被解释:神经元的输出值越大,则该神经元对应的类别是真实类别的可能性更高。
另外,softmax不仅把神经元输出构造成概率分布,而且还起到了归一化的作用,适用于很多需要进行归一化处理的分类问题。
由于softmax在ANN算法中的求导结果比较特别,分为两种情况。希望能帮助到正在学习此类算法的朋友们。求导过程如下所示:
2. softmax配合log似然代价函数训练ANN
在上一篇博文“交叉熵代价函数”中讲到,二次代价函数在训练ANN时可能会导致训练速度变慢的问题。那就是,初始的输出值离真实值越远,训练速度就越慢。这个问题可以通过采用交叉熵代价函数来解决。其实,这个问题也可以采用另外一种方法解决,那就是采用softmax激活函数,并采用log似然代价函数(log-likelihood cost function)来解决。
log似然代价函数的公式为:
其中,
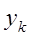
我们来简单理解一下这个代价函数的含义。在ANN中输入一个样本,那么只有一个神经元对应了该样本的正确类别;若这个神经元输出的概率值越高,则按照以上的代价函数公式,其产生的代价就越小;反之,则产生的代价就越高。
为了检验softmax和这个代价函数也可以解决上述所说的训练速度变慢问题,接下来的重点就是推导ANN的权重w和偏置b的梯度公式。以偏置b为例:
同理可得:
从上述梯度公式可知,softmax函数配合log似然代价函数可以很好地训练ANN,不存在学习速度变慢的问题。
 Softmax与Log似然代价函数
Softmax与Log似然代价函数





 本文介绍了Softmax函数及其在人工神经网络输出层的应用,详细解释了它如何配合Log似然代价函数提高网络训练效率,避免学习速度减慢问题。
本文介绍了Softmax函数及其在人工神经网络输出层的应用,详细解释了它如何配合Log似然代价函数提高网络训练效率,避免学习速度减慢问题。
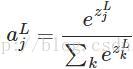
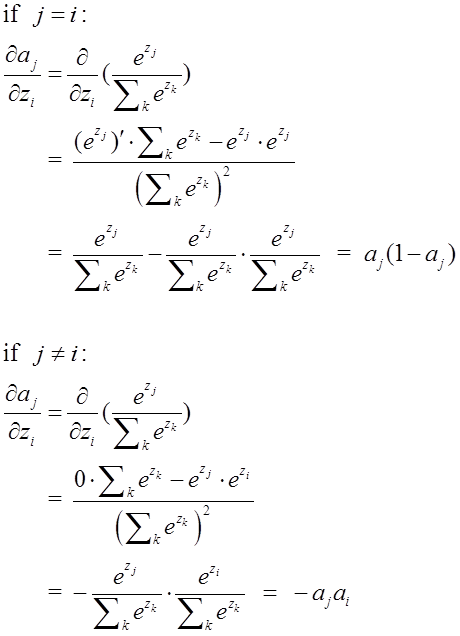

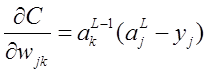
















 2756
2756

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








