高斯分布补充知识

PRML第二章啃到高斯分布的时候就开始不知所云了，看了这篇BlogPRML Chapter 2.3 The Gaussian Distribution之后，觉得讲的很清晰，可惜作者没有写完，于是转过去看了“Methods of Multivariate Analysis ”的第三章。这里是对这些基础知识点的一个记录，用来日后复习。

---

单变量和双变量

单变量的均值和方差

变量y的n个观察量$y_{1}, y_{2}, y_{3}, ... ,y_{n}$，那么样本均值：

$$\overline{y}=\frac{1}{n}\sum_{i=1}^{n}{y_{i}}$$
样本均值 $\overline{y}$永远不会等于变量y的总体均值 $\mu$，尽管随着样本数量的增加 $\overline{y}$会无限接近 $\mu$。 $\overline{y}$是 $\mu$的无偏估计量，因为 $E(\overline{y})=\mu,var(\overline{y})=\frac{\sigma^2}{n}$
样本方差： $s^2=\frac{\sum_{i=1}^{n}(y_{i}-\overline{y})}{n-1}$
同理 $s^2$是总体方差 $\sigma^2$的无偏估计量

双变量的协方差和相关性

协方差

协方差表示两个变量之间的关系，下图中是一些身高和体重的样本数据

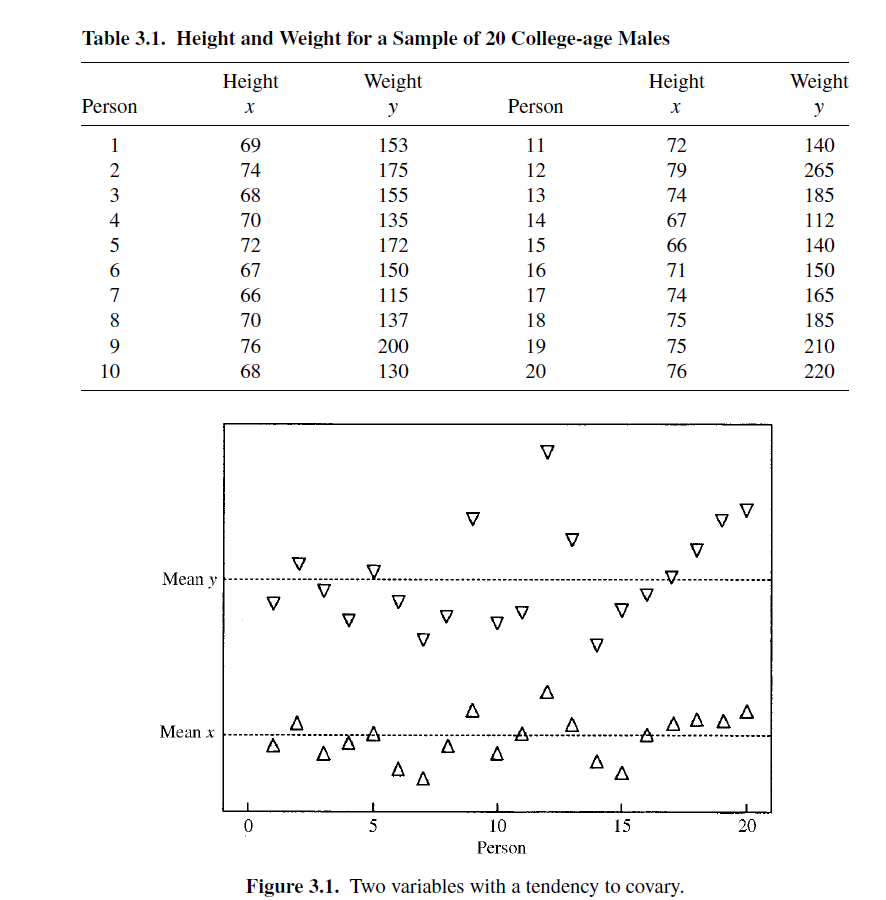
如果把样本用下边的图表示出来，可以发现当身高高于平均值的时候往往体重也会高于平均值，这两者之间可能存在一些相关
两个随机变量x和y之间的关系：

$$E(x+y)=E(x)+E(y)$$
$$E(xy)=E(x)E(y)x和y相互独立$$
如果变量x和y的联合概率密度可以表示为 $p(x,y)=p(x)p(y)$那么变量x和y相互独立，二者相互独立也就是彼此不会相互影响
如果x和y相互独立，那么二者的协方差 $\sigma_{xy}=0$；反之， 如果x,y的协方差$\sigma_{xy}=0$则不能说明二者相互独立
$$\sigma_{xy}=E(xy)-\mu_{x}\mu_{y}=E(x)E(y)-\mu_{x}\mu_{y}-\mu_{x}\mu_{y}=\mu_{x}\mu_{y}-\mu_{x}\mu_{y}=0$$
样本协方差：
$$s_{xy}=\frac{\sum_{i=1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})}{n-1}$$
$$s_{xy}=\frac{\sum_{i=1}^{n}x_{i}y_{i}-n\overline{x}\overline{y}}{n-1}$$
$s_{xy}$永远也不会等于 $\sigma_{xy}$，前者是后者的无偏估计量
样本协方差矩阵只衡量二者之间的线性关系
两组样本的样本协方差为0表示这两组样本正交

相关性

从上边可以看出，如果把变量x和y的样本同时乘以一个系数，那么二者的协方差也会发生变化，由此可以看出协方差与尺度相关，于是引入总体相关性：

$$\rho=corr(x,y)=\frac{\sigma_{xy}}{\sigma_x\sigma_y}=\frac{E[(x-\mu_x)(y-\mu_y)]}{\sqrt{E(x-\mu_x)^2}\sqrt{E(y-\mu_y)^2}}$$
样本相关性：
$$r_{xy}=\frac{s_{xy}}{s_xs_y}=\frac{\sum_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\sum_{i=1}^n(x_i-\overline{x})^2\sum_{i=1}^n(y_i-\overline{y})^2}}$$
仔细看一下：这个式子是和两个向量之间的cos夹角是一致的，所以相关性衡量的也就是两个向量之间的cosine距离
$$cos\theta=\frac{\vec{a}^T\vec{b}}{\sqrt{(\vec{a}^T\vec{a})(\vec{b}^T\vec{b})}}=\frac{\vec{a}^T\vec{b}}{\arrowvert\vec{a}\arrowvert\arrowvert\vec{b}\arrowvert}=r_{xy}$$

---

多变量

均值

向量$\vec{y}$表示一个变量，对变量$\vec{y}$取样n次：

$$y=\begin{pmatrix} y_{i1}\\ y_{i2}\\ ...\\ y_{ip}\\ \end{pmatrix}$$
整个数据矩阵：
$$\bf{Y}=\begin{pmatrix} y_{1}^T\\ y_{2}^T\\ ...\\ y_{n}^T\\ \end{pmatrix} =\begin{pmatrix} y_{11}\qquad{y_{12}}\qquad...\qquad{y_{1p}}\\ y_{21}\qquad{y_{22}}\qquad{...}\qquad{y_{2p}}\\ ...\qquad{...}\qquad{...}\qquad...\\ y_{n1}\qquad{y_{n2}}\qquad...\qquad{y_{np}}\\ \end{pmatrix}$$
$$\overline{y}^T=\frac{1}{n}j^T\bf{Y} \\\overline{y}=\frac{1}{n}\bf{Y^T}{j}$$
j是一个全1的向量
未完待续。。。