红黑树算法的层层剖析与逐步实现
----
作者 July 二零一零年十二月三十一日
本文主要参考：算法导论第二版
本文主要代码：参考算法导论。
本文图片来源：个人手工画成、算法导论原书。
推荐阅读：Leo J. Guibas 和 Robert Sedgewick 于1978年写的关于红黑树的一篇论文。
--------------------------------------------------------------
---------------------------------------------------------------
引言：
昨天下午画红黑树画了好几个钟头，总共10页纸。
特此，再深入剖析红黑树的算法实现，教你如何彻底实现红黑树算法。
经过我上一篇博文，“教你透彻了解红黑树”后，相信大家对红黑树已经有了一定的了解。
个人觉得，这个红黑树，还是比较容易懂的。
不论是插入、还是删除，不论是左旋还是右旋，最终的目的只有一个：
即保持红黑树的5个性质，不得违背。
再次，重述下红黑树的五个性质：
一般的，红黑树，满足一下性质，即只有满足一下性质的树，我们才称之为红黑树：
1）每个结点要么是红的，要么是黑的。
2）根结点是黑的。
3）每个叶结点，即空结点（NIL）是黑的。
4）如果一个结点是红的，那么它的俩个儿子都是黑的。
5）对每个结点，从该结点到其子孙结点的所有路径上包含相同数目的黑结点。
抓住了红黑树的那5个性质，事情就好办多了。
如，
1.红黑红黑，要么是红，要么是黑；
2.根结点是黑；
3.每个叶结点是黑；
4.一个红结点，它的俩个儿子必然都是黑的；
5.每一条路径上，黑结点的数目等同。
五条性质，合起来，来句顺口溜就是：（1）红黑 （2）黑 （3）黑 （4&5）红->黑 黑。
本文所有的文字，都是参照我昨下午画的十张纸（即我拍的照片）与算法导论来写的。
希望，你依照此文一点一点的往下看，看懂此文后，你对红黑树的算法了解程度，一定大增不少。
ok，现在咱们来具体深入剖析红黑树的算法，并教你逐步实现此算法。
此教程分为10个部分，每一个部分作为一个小节。且各小节与我给的十张照片一一对应。
一、左旋与右旋
先明确一点：为什么要左旋?
因为红黑树插入或删除结点后，树的结构发生了变化，从而可能会破坏红黑树的性质。
为了维持插入、或删除结点后的树，仍然是一颗红黑树，所以有必要对树的结构做部分调整，从而恢复红黑树的原本性质。
而为了恢复红黑性质而作的动作包括：
结点颜色的改变(重新着色)，和结点的调整。
这部分结点调整工作，改变指针结构，即是通过左旋或右旋而达到目的。
从而使插入、或删除结点的树重新成为一颗新的红黑树。
ok，请看下图：
如上图所示，‘找茬’
如果你看懂了上述俩幅图有什么区别时，你就知道什么是“左旋”，“右旋”。
在此，着重分析左旋算法：
左旋，如图所示（左->右），以x->y之间的链为“支轴”进行，
使y成为该新子树的根，x成为y的左孩子，而y的左孩子则成为x的右孩子。
算法很简单，还有注意一点，各个结点从左往右，不论是左旋前还是左旋后，结点大小都是从小到大。
左旋代码实现，分三步（注意我给的注释）：
The pseudocode for LEFT-ROTATE assumes that right[x] ≠ nil[T] and that the root's parent is nil[T].
LEFT-ROTATE(T, x)
1 y ← right[x] ▹ Set y.
2 right[x] ← left[y] //开始变化，y的左孩子成为x的右孩子
3 if left[y] ！=nil[T]
4 then p[left[y]] <- x
5 p[y] <- p[x] //y成为x的父结点
6 if p[x] = nil[T]
7 then root[T] <- y
8 else if x = left[p[x]]
9 then left[p[x]] ← y
10 else right[p[x]] ← y
11 left[y] ← x //x成为y的左孩子（一月三日修正）
12 p[x] ← y
//注，此段左旋代码，原书第一版英文版与第二版中文版，有所出入。
//个人觉得，第二版更精准。所以，此段代码以第二版中文版为准。
左旋、右旋都是对称的，且都是在O（1）时间内完成。因为旋转时只有指针被改变，而结点中的所有域都保持不变。
最后，贴出昨下午关于此左旋算法所画的图：
左旋（第2张图）：
//此图有点bug。第4行的注释移到第11行。如上述代码所示。（一月三日修正）
二、左旋的一个实例
不做过多介绍，看下副图，一目了然。
LEFT-ROTATE(T, x)的操作过程（第3张图）：
---------------------
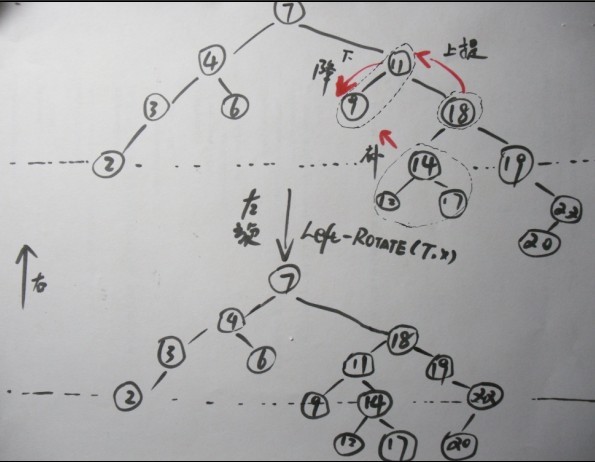
提醒，看下文之前，请首先务必明确，区别以下俩种操作：
1.红黑树插入、删除结点的操作
//如插入中，红黑树插入结点操作：RB-INSERT(T, z)。
2.红黑树已经插入、删除结点之后，
为了保持红黑树原有的红黑性质而做的恢复与保持红黑性质的操作。
//如插入中，为了恢复和保持原有红黑性质，所做的工作：RB-INSERT-FIXUP(T, z)。
ok，请继续。
三、红黑树的插入算法实现
RB-INSERT(T, z) //注意我给的注释...
1 y ← nil[T] // y 始终指向 x 的父结点。
2 x ← root[T] // x 指向当前树的根结点，
3 while x ≠ nil[T]
4 do y ← x
5 if key[z] < key[x] //向左，向右..
6 then x ← left[x]
7 else x ← right[x] // 为了找到合适的插入点，x 探路跟踪路径，直到x成为NIL 为止。
8 p[z] ← y // y置为 插入结点z 的父结点。
9 if y = nil[T]
10 then root[T] ← z
11 else if key[z] < key[y]
12 then left[y] ← z
13 else right[y] ← z //此 8-13行，置z 相关的指针。
14 left[z] ← nil[T]
15 right[z] ← nil[T] //设为空，
16 color[z] ← RED //将新插入的结点z作为红色
17 RB-INSERT-FIXUP(T, z) //因为将z着为红色，可能会违反某一红黑性质，
//所以需要调用RB-INSERT-FIXUP(T, z)来保持红黑性质。
17 行的RB-INSERT-FIXUP(T, z) ，在下文会得到着重而具体的分析。
还记得，我开头说的那句话么，
是的，时刻记住，不论是左旋还是右旋，不论是插入、还是删除，都要记得恢复和保持红黑树的5个性质。
四、调用RB-INSERT-FIXUP(T, z)来保持和恢复红黑性质
RB-INSERT-FIXUP(T, z)
1 while color[p[z]] = RED
2 do if p[z] = left[p[p[z]]]
3 then y ← right[p[p[z]]]
4 if color[y] = RED
5 then color[p[z]] ← BLACK ▹ Case 1
6 color[y] ← BLACK ▹ Case 1
7 color[p[p[z]]] ← RED ▹ Case 1
8 z ← p[p[z]] ▹ Case 1
9 else if z = right[p[z]]
10 then z ← p[z] ▹ Case 2
11 LEFT-ROTATE(T, z) ▹ Case 2
12 color[p[z]] ← BLACK ▹ Case 3
13 color[p[p[z]]] ← RED ▹ Case 3
14 RIGHT-ROTATE(T, p[p[z]]) ▹ Case 3
15 else (same as then clause
with "right" and "left" exchanged)
16 color[root[T]] ← BLACK
//第4张图略：
五、红黑树插入的三种情况，即RB-INSERT-FIXUP(T, z)。操作过程（第5张）：
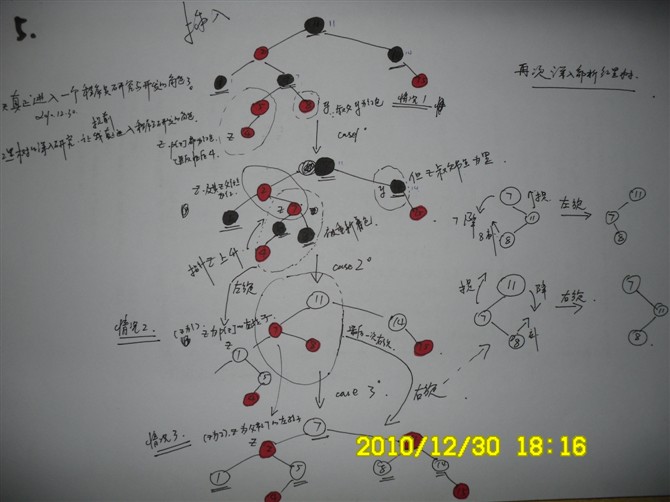
//这幅图有个小小的问题，读者可能会产生误解。图中左侧所表明的情况2、情况3所标的位置都要标上一点。
//请以图中的标明的case1、case2、case3为准。一月三日。
六、红黑树插入的第一种情况（RB-INSERT-FIXUP(T, z)代码的具体分析一）
为了保证阐述清晰，重述下RB-INSERT-FIXUP(T, z)的源码：
RB-INSERT-FIXUP(T, z)
1 while color[p[z]] = RED
2 do if p[z] = left[p[p[z]]]
3 then y ← right[p[p[z]]]
4 if color[y] = RED
5 then color[p[z]] ← BLACK ▹ Case 1
6 color[y] ← BLACK ▹ Case 1
7 color[p[p[z]]] ← RED ▹ Case 1
8 z ← p[p[z]] ▹ Case 1
9 else if z = right[p[z]]
10 then z ← p[z] ▹ Case 2
11 LEFT-ROTATE(T, z) ▹ Case 2
12 color[p[z]] ← BLACK ▹ Case 3
13 color[p[p[z]]] ← RED ▹ Case 3
14 RIGHT-ROTATE(T, p[p[z]]) ▹ Case 3
15 else (same as then clause
with "right" and "left" exchanged)
16 color[root[T]] ← BLACK
//case1表示情况1，case2表示情况2，case3表示情况3.
ok，如上所示，相信，你已看到了。
咱们，先来透彻分析红黑树插入的第一种情况：
插入情况1，z的叔叔y是红色的。
第一种情况，即上述代码的第5-8行：
5 then color[p[z]] ← BLACK ▹ Case 1
6 color[y] ← BLACK ▹ Case 1
7 color[p[p[z]]] ← RED ▹ Case 1
8 z ← p[p[z]] ▹ Case 1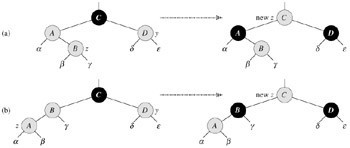
如上图所示，a：z为右孩子，b：z为左孩子。
只有p[z]和y（上图a中A为p[z]，D为z，上图b中，B为p[z]，D为y）都是红色的时候，才会执行此情况1.
咱们分析下上图的a情况，即z为右孩子时
因为p[p[z]]，即c是黑色，所以将p[z]、y都着为黑色（如上图a部分的右边），
此举解决z、p[z]都是红色的问题，将p[p[z]]着为红色，则保持了性质5.
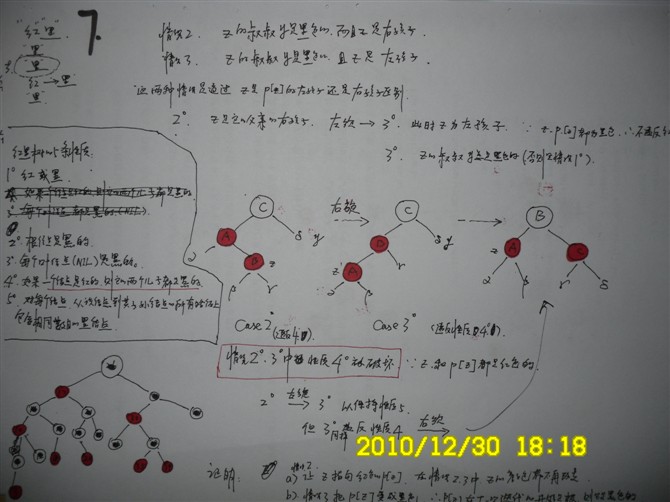
ok，看下我昨天画的图（第6张）：
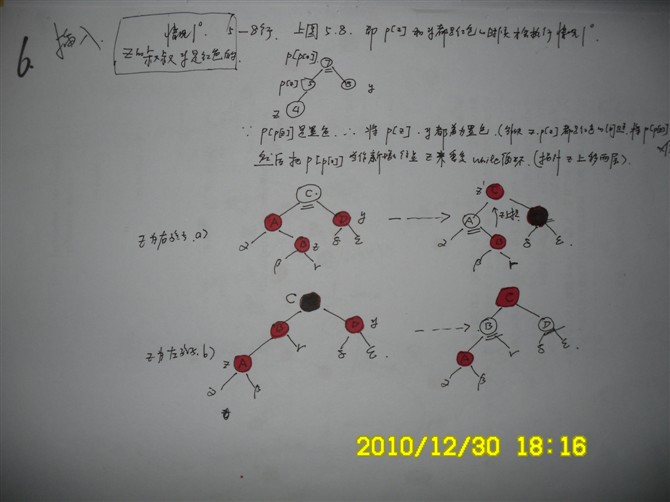
红黑树插入的第一种情况完。
七、红黑树插入的第二种、第三种情况
插入情况2：z的叔叔y是黑色的，且z是右孩子
插入情况3：z的叔叔y是黑色的，且z是左孩子
这俩种情况，是通过z是p[z]的左孩子，还是右孩子区别的。
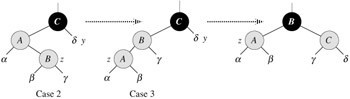
参照上图，针对情况2，z是她父亲的右孩子，则为了保持红黑性质，左旋则变为情况3，此时z为左孩子，
因为z、p[z]都为黑色，所以不违反红黑性质（注，情况3中，z的叔叔y是黑色的，否则此种情况就变成上述情况1 了）。
ok，我们已经看出来了，情况2，情况3都违反性质4（一个红结点的俩个儿子都是黑色的）。
所以情况2->左旋后->情况3，此时情况3同样违反性质4，所以情况3->右旋，得到上图的最后那部分。
注，情况2、3都只违反性质4，其它的性质1、2、3、5都不违背。
好的，最后，看下我画的图（第7张）：
八、接下来，进入红黑树的删除部分。
RB-DELETE(T, z)
1 if left[z] = nil[T] or right[z] = nil[T]
2 then y ← z
3 else y ← TREE-SUCCESSOR(z)
4 if left[y] ≠ nil[T]
5 then x ← left[y]
6 else x ← right[y]
7 p[x] ← p[y]
8 if p[y] = nil[T]
9 then root[T] ← x
10 else if y = left[p[y]]
11 then left[p[y]] ← x
12 else right[p[y]] ← x
13 if y 3≠ z
14 then key[z] ← key[y]
15 copy y's satellite data into z
16 if color[y] = BLACK //如果y是黑色的，
17 then RB-DELETE-FIXUP(T, x) //则调用RB-DELETE-FIXUP(T, x)
18 return y //如果y不是黑色，是红色的，则当y被删除时，红黑性质仍然得以保持。不做操作，返回。
//因为：1.树种各结点的黑高度都没有变化。2.不存在俩个相邻的红色结点。
//3.因为入宫y是红色的，就不可能是根。所以，根仍然是黑色的。
ok，第8张图，不必贴了。
九、红黑树删除之4种情况，RB-DELETE-FIXUP(T, x)之代码
RB-DELETE-FIXUP(T, x)
1 while x ≠ root[T] and color[x] = BLACK
2 do if x = left[p[x]]
3 then w ← right[p[x]]
4 if color[w] = RED
5 then color[w] ← BLACK ▹ Case 1
6 color[p[x]] ← RED ▹ Case 1
7 LEFT-ROTATE(T, p[x]) ▹ Case 1
8 w ← right[p[x]] ▹ Case 1
9 if color[left[w]] = BLACK and color[right[w]] = BLACK
10 then color[w] ← RED ▹ Case 2
11 x ← p[x] ▹ Case 2
12 else if color[right[w]] = BLACK
13 then color[left[w]] ← BLACK ▹ Case 3
14 color[w] ← RED ▹ Case 3
15 RIGHT-ROTATE(T, w) ▹ Case 3
16 w ← right[p[x]] ▹ Case 3
17 color[w] ← color[p[x]] ▹ Case 4
18 color[p[x]] ← BLACK ▹ Case 4
19 color[right[w]] ← BLACK ▹ Case 4
20 LEFT-ROTATE(T, p[x]) ▹ Case 4
21 x ← root[T] ▹ Case 4
22 else (same as then clause with "right" and "left" exchanged)
23 color[x] ← BLACK
ok，很清楚，在此，就不贴第9张图了。
在下文的红黑树删除的4种情况，详细、具体分析了上段代码。
十、红黑树删除的4种情况
情况1：x的兄弟w是红色的。
情况2：x的兄弟w是黑色的，且w的俩个孩子都是黑色的。
情况3：x的兄弟w是黑色的，w的左孩子是红色，w的右孩子是黑色。
情况4：x的兄弟w是黑色的，且w的右孩子时红色的。
操作流程图：
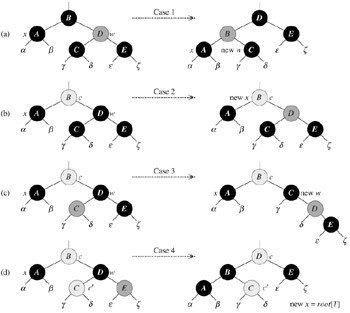
ok，简单分析下，红黑树删除的4种情况：
针对情况1：x的兄弟w是红色的。
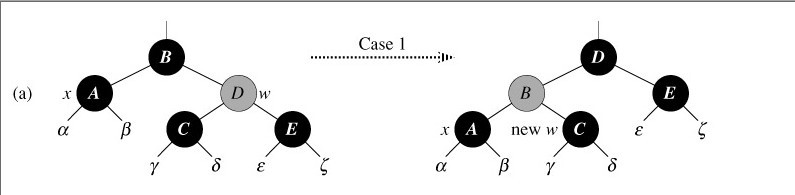
5 then color[w] ← BLACK ▹ Case 1
6 color[p[x]] ← RED ▹ Case 1
7 LEFT-ROTATE(T, p[x]) ▹ Case 1
8 w ← right[p[x]] ▹ Case 1
对策：改变w、p[z]颜色，再对p[x]做一次左旋，红黑性质得以继续保持。
x的新兄弟new w是旋转之前w的某个孩子，为黑色。
所以，情况1转化成情况2或3、4。
针对情况2：x的兄弟w是黑色的，且w的俩个孩子都是黑色的。
10 then color[w] ← RED ▹ Case 2
11 x <-p[x] ▹ Case 2
如图所示，w的俩个孩子都是黑色的，
对策：因为w也是黑色的，所以x和w中得去掉一黑色，最后，w变为红。
p[x]为新结点x，赋给x，x<-p[x]。
针对情况3：x的兄弟w是黑色的，w的左孩子是红色，w的右孩子是黑色。
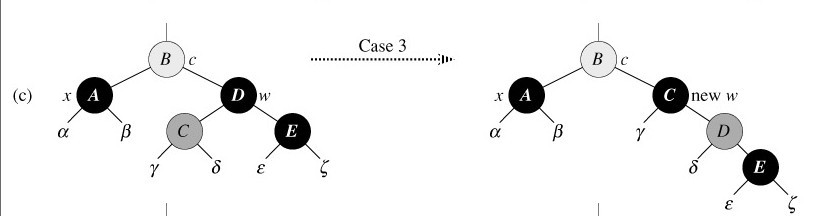
13 then color[left[w]] ← BLACK ▹ Case 3
14 color[w] ← RED ▹ Case 3
15 RIGHT-ROTATE(T, w) ▹ Case 3
16 w ← right[p[x]] ▹ Case 3
w为黑，其左孩子为红，右孩子为黑
对策：交换w和和其左孩子left[w]的颜色。 即上图的D、C颜色互换。:D。
并对w进行右旋，而红黑性质仍然得以保持。
现在x的新兄弟w是一个有红色右孩子的黑结点，于是将情况3转化为情况4.
针对情况4：x的兄弟w是黑色的，且w的右孩子时红色的。
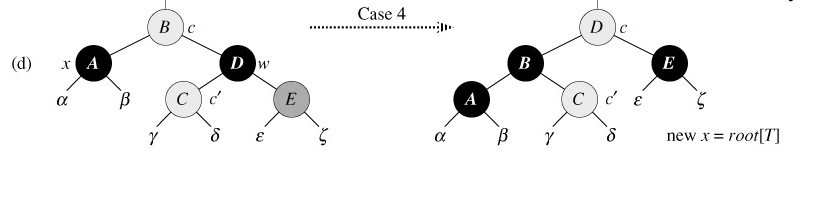
17 color[w] ← color[p[x]] ▹ Case 4
18 color[p[x]] ← BLACK ▹ Case 4
19 color[right[w]] ← BLACK ▹ Case 4
20 LEFT-ROTATE(T, p[x]) ▹ Case 4
21 x ← root[T] ▹ Case 4
x的兄弟w为黑色，且w的右孩子为红色。
对策：做颜色修改，并对p[x]做一次旋转，可以去掉x的额外黑色，来把x变成单独的黑色，此举不破坏红黑性质。
将x置为根后，循环结束。
最后，贴上最后的第10张图：
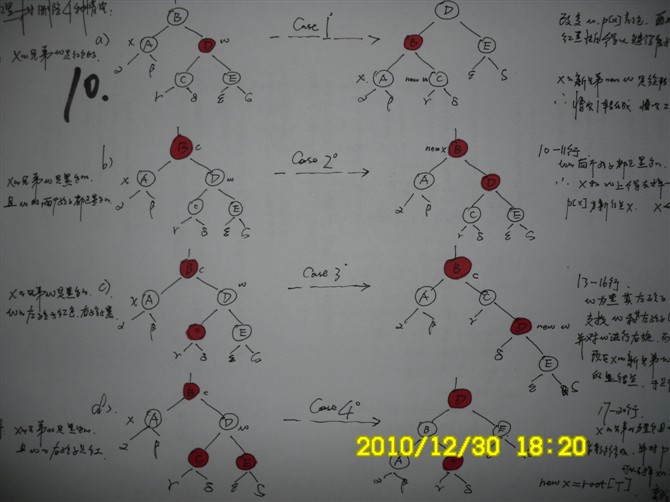
ok，红黑树删除的4中情况，分析完成。
结语：只要牢牢抓住红黑树的5个性质不放，而不论是树的左旋还是右旋，
不论是红黑树的插入、还是删除，都只为了保持和修复红黑树的5个性质而已。
顺祝各位， 元旦快乐。完。
July、二零一零年十二月三十日。
-------------------------------------------------------
扩展阅读：Left-Leaning Red-Black Trees, Dagstuhl Workshop on Data Structures, Wadern, Germany, February, 2008.
直接下载：http://www.cs.princeton.edu/~rs/talks/LLRB/RedBlack.pdf
版权声明
版权所有，侵权必究。
167
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
