红黑树的C++完整实现源码
作者:July、saturnman。
时间:二零一一年三月二十九日。
出处:http://blog.csdn.net/v_JULY_v。
声明:版权所有,侵权必究。
-------------------------------------------
前言:
红黑树系列文章已经写到第5篇了。虽然第三篇文章:红黑树的c源码实现与剖析,用c语言完整实现过红黑树,但个人感觉,代码还是不够清晰。特此,再奉献出一份c++的完整实现源码,以飨读者。
此份c++实现源码,代码紧凑了许多,也清晰了不少,同时采取c++类实现的方式,代码也更容易维护以及重用。ok,有任何问题,欢迎指正。
第一部分、红黑树的c++完整实现源码
本文包含红黑树c++实现的完整源码,所有的解释都含在注释中,所有的有关红黑树的原理及各种插入、删除操作的情况,都已在本人的红黑树系列的前4篇文章中,一一阐述。且在此红黑树系列第五篇文章中:红黑树从头至尾插入和删除结点的全程演示图,把所有的插入、删除情况都一一展示尽了。
因此,有关红黑树的全部原理,请参考其它文章,重点可参考此文:红黑树算法的实现与剖析。因此,相关原理,本文不再赘述。
ok,以下,即是红黑树c++实现的全部源码,先是RBTree.h,然后是RBTree.cpp。
RBTree.h
//file RBTree.h
//written by saturnman,20101008。
//updated by July,20110329。
/*-----------------------------------------------
版权声明:
July和saturnman对此份红黑树的c++实现代码享有全部的版权,
谢绝转载,侵权必究。
------------------------------------------------*/
#ifndef _RB_TREE_H_
#define _RB_TREE_H_
#include<iostream>
#include<string>
#include<sstream>
#include<fstream>
using namespace std;
template<class KEY, class U>
class RB_Tree
{
private:
RB_Tree(const RB_Tree& input){}
const RB_Tree& operator=(const RB_Tree& input){}
private:
enum COLOR{ RED, BLACK };
class RB_Node
{
public:
RB_Node()
{
//RB_COLOR = BLACK;
right = NULL;
left = NULL;
parent = NULL;
}
COLOR RB_COLOR;
RB_Node* right;
RB_Node* left;
RB_Node* parent;
KEY key;
U data;
};
public:
RB_Tree()
{
this->m_nullNode = new RB_Node();
this->m_root = m_nullNode;
this->m_nullNode->right = this->m_root;
this->m_nullNode->left = this->m_root;
this->m_nullNode->parent = this->m_root;
this->m_nullNode->RB_COLOR = BLACK;
}
bool Empty()
{
if (this->m_root == this->m_nullNode)
{
return true;
}
else
{
return false;
}
}
//查找key
RB_Node* find(KEY key)
{
RB_Node* index = m_root;
while (index != m_nullNode)
{
if (key<index->key)
{
index = index->left; //比当前的小,往左
}
else if (key>index->key)
{
index = index->right; //比当前的大,往右
}
else
{
break;
}
}
return index;
}
//--------------------------插入结点总操作----------------------------------
//全部的工作,都在下述伪代码中:
/*RB-INSERT(T, z)
1 y ← nil[T] // y 始终指向 x 的父结点。
2 x ← root[T] // x 指向当前树的根结点,
3 while x ≠ nil[T]
4 do y ← x
5 if key[z] < key[x] //向左,向右..
6 then x ← left[x]
7 else x ← right[x] //为了找到合适的插入点,x探路跟踪路径,直到x成为NIL 为止。
8 p[z] ← y //y置为 插入结点z 的父结点。
9 if y = nil[T]
10 then root[T] ← z
11 else if key[z] < key[y]
12 then left[y] ← z
13 else right[y] ← z //此 8-13行,置z 相关的指针。
14 left[z] ← nil[T]
15 right[z] ← nil[T] //设为空,
16 color[z] ← RED //将新插入的结点z作为红色
17 RB-INSERT-FIXUP(T, z)
*/
//因为将z着为红色,可能会违反某一红黑性质,
//所以需要调用下面的RB-INSERT-FIXUP(T, z)来保持红黑性质。
bool Insert(KEY key, U data)
{
RB_Node* insert_point = m_nullNode;
RB_Node* index = m_root;
while (index != m_nullNode)
{
insert_point = index;
if (key<index->key)
{
index = index->left;
}
else if (key>index->key)
{
index = index->right;
}
else
{
return false;
}
}
RB_Node* insert_node = new RB_Node();
insert_node->key = key;
insert_node->data = data;
insert_node->RB_COLOR = RED;
insert_node->right = m_nullNode;
insert_node->left = m_nullNode;
if (insert_point == m_nullNode) //如果插入的是一颗空树
{
m_root = insert_node;
m_root->parent = m_nullNode;
m_nullNode->left = m_root;
m_nullNode->right = m_root;
m_nullNode->parent = m_root;
}
else
{
if (key < insert_point->key)
{
insert_point->left = insert_node;
}
else
{
insert_point->right = insert_node;
}
insert_node->parent = insert_point;
}
InsertFixUp(insert_node); //调用InsertFixUp修复红黑树性质。
}
//---------------------插入结点性质修复--------------------------------
//3种插入情况,都在下面的伪代码中(未涉及到所有全部的插入情况)。
/*
RB-INSERT-FIXUP(T, z)
1 while color[p[z]] = RED
2 do if p[z] = left[p[p[z]]]
3 then y ← right[p[p[z]]]
4 if color[y] = RED
5 then color[p[z]] ← BLACK ? Case 1
6 color[y] ← BLACK ? Case 1
7 color[p[p[z]]] ← RED ? Case 1
8 z ← p[p[z]] ? Case 1
9 else if z = right[p[z]]
10 then z ← p[z] ? Case 2
11 LEFT-ROTATE(T, z) ? Case 2
12 color[p[z]] ← BLACK ? Case 3
13 color[p[p[z]]] ← RED ? Case 3
14 RIGHT-ROTATE(T, p[p[z]]) ? Case 3
15 else (same as then clause with "right" and "left" exchanged)
16 color[root[T]] ← BLACK
*/
//然后的工作,就非常简单了,即把上述伪代码改写为下述的c++代码:
void InsertFixUp(RB_Node* node)
{
while (node->parent->RB_COLOR == RED)
{
if (node->parent == node->parent->parent->left) //
{
RB_Node* uncle = node->parent->parent->right;
if (uncle->RB_COLOR == RED) //插入情况1,z的叔叔y是红色的。
{
node->parent->RB_COLOR = BLACK;
uncle->RB_COLOR = BLACK;
node->parent->parent->RB_COLOR = RED;
node = node->parent->parent;
}
else if (uncle->RB_COLOR == BLACK) //插入情况2:z的叔叔y是黑色的,。
{
if (node == node->parent->right) //且z是右孩子
{
node = node->parent;
RotateLeft(node);
}
//else //插入情况3:z的叔叔y是黑色的,但z是左孩子。
//{
node->parent->RB_COLOR = BLACK;
node->parent->parent->RB_COLOR = RED;
RotateRight(node->parent->parent);
//}
}
}
else //这部分是针对为插入情况1中,z的父亲现在作为祖父的右孩子了的情况,而写的。
//15 else (same as then clause with "right" and "left" exchanged)
{
RB_Node* uncle = node->parent->parent->left;
if (uncle->RB_COLOR == RED)
{
node->parent->RB_COLOR = BLACK;
uncle->RB_COLOR = BLACK;
uncle->parent->RB_COLOR = RED;
node = node->parent->parent;
}
else if (uncle->RB_COLOR == BLACK)
{
if (node == node->parent->left)
{
node = node->parent;
RotateRight(node); //与上述代码相比,左旋改为右旋
}
//else
//{
node->parent->RB_COLOR = BLACK;
node->parent->parent->RB_COLOR = RED;
RotateLeft(node->parent->parent); //右旋改为左旋,即可。
//}
}
}
}
m_root->RB_COLOR = BLACK;
}
//左旋代码实现
bool RotateLeft(RB_Node* node)
{
if (node == m_nullNode || node->right == m_nullNode)
{
return false;//can't rotate
}
RB_Node* lower_right = node->right;
lower_right->parent = node->parent;
node->right = lower_right->left;
if (lower_right->left != m_nullNode)
{
lower_right->left->parent = node;
}
if (node->parent == m_nullNode) //rotate node is root
{
m_root = lower_right;
m_nullNode->left = m_root;
m_nullNode->right = m_root;
//m_nullNode->parent = m_root;
}
else
{
if (node == node->parent->left)
{
node->parent->left = lower_right;
}
else
{
node->parent->right = lower_right;
}
}
node->parent = lower_right;
lower_right->left = node;
}
//右旋代码实现
bool RotateRight(RB_Node* node)
{
if (node == m_nullNode || node->left == m_nullNode)
{
return false;//can't rotate
}
RB_Node* lower_left = node->left;
node->left = lower_left->right;
lower_left->parent = node->parent;
if (lower_left->right != m_nullNode)
{
lower_left->right->parent = node;
}
if (node->parent == m_nullNode) //node is root
{
m_root = lower_left;
m_nullNode->left = m_root;
m_nullNode->right = m_root;
//m_nullNode->parent = m_root;
}
else
{
if (node == node->parent->right)
{
node->parent->right = lower_left;
}
else
{
node->parent->left = lower_left;
}
}
node->parent = lower_left;
lower_left->right = node;
}
//--------------------------删除结点总操作----------------------------------
//伪代码,不再贴出,详情,请参考此红黑树系列第二篇文章:
//经典算法研究系列:五、红黑树算法的实现与剖析:
//http://blog.csdn.net/v_JULY_v/archive/2010/12/31/6109153.aspx。
bool Delete(KEY key)
{
RB_Node* delete_point = find(key);
if (delete_point == m_nullNode)
{
return false;
}
if (delete_point->left != m_nullNode && delete_point->right != m_nullNode)
{
RB_Node* successor = InOrderSuccessor(delete_point);
delete_point->data = successor->data;
delete_point->key = successor->key;
delete_point = successor;
}
RB_Node* delete_point_child;
if (delete_point->right != m_nullNode)
{
delete_point_child = delete_point->right;
}
else if (delete_point->left != m_nullNode)
{
delete_point_child = delete_point->left;
}
else
{
delete_point_child = m_nullNode;
}
delete_point_child->parent = delete_point->parent;
if (delete_point->parent == m_nullNode)//delete root node
{
m_root = delete_point_child;
m_nullNode->parent = m_root;
m_nullNode->left = m_root;
m_nullNode->right = m_root;
}
else if (delete_point == delete_point->parent->right)
{
delete_point->parent->right = delete_point_child;
}
else
{
delete_point->parent->left = delete_point_child;
}
if (delete_point->RB_COLOR == BLACK && !(delete_point_child == m_nullNode && delete_point_child->parent == m_nullNode))
{
DeleteFixUp(delete_point_child);
}
delete delete_point;
return true;
}
//---------------------删除结点性质修复-----------------------------------
//所有的工作,都在下述23行伪代码中:
/*
RB-DELETE-FIXUP(T, x)
1 while x ≠ root[T] and color[x] = BLACK
2 do if x = left[p[x]]
3 then w ← right[p[x]]
4 if color[w] = RED
5 then color[w] ← BLACK ? Case 1
6 color[p[x]] ← RED ? Case 1
7 LEFT-ROTATE(T, p[x]) ? Case 1
8 w ← right[p[x]] ? Case 1
9 if color[left[w]] = BLACK and color[right[w]] = BLACK
10 then color[w] ← RED ? Case 2
11 x p[x] ? Case 2
12 else if color[right[w]] = BLACK
13 then color[left[w]] ← BLACK ? Case 3
14 color[w] ← RED ? Case 3
15 RIGHT-ROTATE(T, w) ? Case 3
16 w ← right[p[x]] ? Case 3
17 color[w] ← color[p[x]] ? Case 4
18 color[p[x]] ← BLACK ? Case 4
19 color[right[w]] ← BLACK ? Case 4
20 LEFT-ROTATE(T, p[x]) ? Case 4
21 x ← root[T] ? Case 4
22 else (same as then clause with "right" and "left" exchanged)
23 color[x] ← BLACK
*/
//接下来的工作,很简单,即把上述伪代码改写成c++代码即可。
void DeleteFixUp(RB_Node* node)
{
while (node != m_root && node->RB_COLOR == BLACK)
{
if (node == node->parent->left)
{
RB_Node* brother = node->parent->right;
if (brother->RB_COLOR == RED) //情况1:x的兄弟w是红色的。
{
brother->RB_COLOR = BLACK;
node->parent->RB_COLOR = RED;
RotateLeft(node->parent);
}
else //情况2:x的兄弟w是黑色的,
{
if (brother->left->RB_COLOR == BLACK && brother->right->RB_COLOR == BLACK)
//且w的俩个孩子都是黑色的。
{
brother->RB_COLOR = RED;
node = node->parent;
}
else if (brother->right->RB_COLOR == BLACK)
//情况3:x的兄弟w是黑色的,w的右孩子是黑色(w的左孩子是红色)。
{
brother->RB_COLOR = RED;
brother->left->RB_COLOR = BLACK;
RotateRight(brother);
}
//else if(brother->right->RB_COLOR == RED)
//情况4:x的兄弟w是黑色的,且w的右孩子时红色的。
//{
brother->RB_COLOR = node->parent->RB_COLOR;
node->parent->RB_COLOR = BLACK;
brother->right->RB_COLOR = BLACK;
RotateLeft(node->parent);
node = m_root;
//}
}
}
else //下述情况针对上面的情况1中,node作为右孩子而阐述的。
//22 else (same as then clause with "right" and "left" exchanged)
//同样,原理一致,只是遇到左旋改为右旋,遇到右旋改为左旋,即可。其它代码不变。
{
RB_Node* brother = node->parent->left;
if (brother->RB_COLOR == RED)
{
brother->RB_COLOR = BLACK;
node->parent->RB_COLOR = RED;
RotateRight(node->parent);
}
else
{
if (brother->left->RB_COLOR == BLACK && brother->right->RB_COLOR == BLACK)
{
brother->RB_COLOR = RED;
node = node->parent;
}
else if (brother->left->RB_COLOR == BLACK)
{
brother->RB_COLOR = RED;
brother->right->RB_COLOR = BLACK;
RotateLeft(brother);
}
//else if(brother->left->RB_COLOR==RED)
//{
brother->RB_COLOR = node->parent->RB_COLOR;
node->parent->RB_COLOR = BLACK;
brother->left->RB_COLOR = BLACK;
RotateRight(node->parent);
node = m_root;
//}
}
}
}
m_nullNode->parent = m_root; //最后将node置为根结点,
node->RB_COLOR = BLACK; //并改为黑色。
}
//
inline RB_Node* InOrderPredecessor(RB_Node* node)
{
if (node == m_nullNode) //null node has no predecessor
{
return m_nullNode;
}
RB_Node* result = node->left; //get node's left child
while (result != m_nullNode) //try to find node's left subtree's right most node
{
if (result->right != m_nullNode)
{
result = result->right;
}
else
{
break;
}
} //after while loop result==null or result's right child is null
if (result == m_nullNode)
{
RB_Node* index = node->parent;
result = node;
while (index != m_nullNode && result == index->left)
{
result = index;
index = index->parent;
}
result = index; // first right parent or null
}
return result;
}
//
inline RB_Node* InOrderSuccessor(RB_Node* node)
{
if (node == m_nullNode) //null node has no successor
{
return m_nullNode;
}
RB_Node* result = node->right; //get node's right node
while (result != m_nullNode) //try to find node's right subtree's left most node
{
if (result->left != m_nullNode)
{
result = result->left;
}
else
{
break;
}
} //after while loop result==null or result's left child is null
if (result == m_nullNode)
{
RB_Node* index = node->parent;
result = node;
while (index != m_nullNode && result == index->right)
{
result = index;
index = index->parent;
}
result = index; //first parent's left or null
}
return result;
}
//debug
void InOrderTraverse()
{
InOrderTraverse(m_root);
}
void CreateGraph(string filename)
{
//delete
}
void InOrderCreate(ofstream& file, RB_Node* node)
{
//delete
}
void InOrderTraverse(RB_Node* node)
{
if (node == m_nullNode)
{
return;
}
else
{
InOrderTraverse(node->left);
cout << node->key << endl;
InOrderTraverse(node->right);
}
}
~RB_Tree()
{
clear(m_root);
delete m_nullNode;
}
private:
// utility function for destructor to destruct object;
void clear(RB_Node* node)
{
if (node == m_nullNode)
{
return;
}
else
{
clear(node->left);
clear(node->right);
delete node;
}
}
private:
RB_Node *m_nullNode;
RB_Node *m_root;
};
#endif /*_RB_TREE_H_*///file RBTree.cpp
//written by saturnman,20101008。
//updated by July,20110329。
//所有的头文件都已补齐,现在您可以直接复制此份源码上机验证了(版权所有,侵权必究)。
//July、updated,2011.05.06。
#include<iostream>
#include<algorithm>
#include<iterator>
#include<vector>
#include<sstream>
#include"RBTree.h" //如果.h文件,和cpp文件放在一个文件里,此句去掉
using namespace std;
int main()
{
RB_Tree<int,int> tree;
vector<int> v;
for(int i=0;i<20;++i)
{
v.push_back(i);
}
random_shuffle(v.begin(),v.end());
copy(v.begin(),v.end(),ostream_iterator<int>(cout," "));
cout<<endl;
stringstream sstr;
for(i=0;i<v.size();++i)
{
tree.Insert(v[i],i);
cout<<"insert:"<<v[i]<<endl; //添加结点
}
for(i=0;i<v.size();++i)
{
cout<<"Delete:"<<v[i]<<endl;
tree.Delete(v[i]); //删除结点
tree.InOrderTraverse();
}
cout<<endl;
tree.InOrderTraverse();
return 0;
}运行效果图(先是一一插入各结点,然后再删除所有的结点):


第二部分、程序有bug?
2.1、红黑树要求绝对平衡么?
据网友鑫反馈,上述c++源码虽说从上面的测试结果来看,没有问题。但程序还是有隐藏的bug,下面,分两个步骤再来测试下此段源码:
1、首先在RBTree.h的最后里添加下述代码:
2、改写RBTree.cpp文件,如下:
后经测试,结果,的确有误,即依次插入以下节点,12,1,9,0,2,11,7后,红黑树变为如下: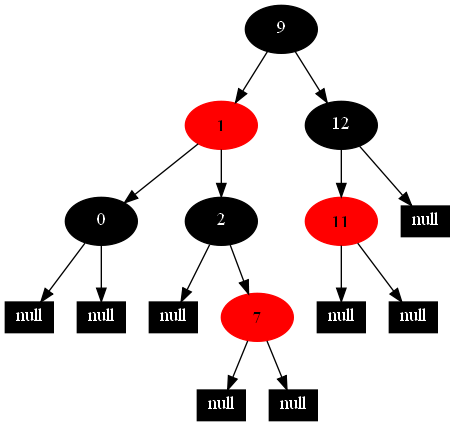
然后删除根节点9,经过上述程序运行后,运行结果,如下:
即上述运行结果,所对应的红黑树的状态如下(此时,红黑树已经不再平衡,存在的问题确实已经很明显了):
是的,如你所见,上述程序删除根节点9之后,正确的红黑树的状态应该为7代替根节点9,7成为新的根节点,且节点7着为黑色,而上述结果则是完全错误,红黑树已经完全不平衡。至此,终于发现,此c++程序存在隐藏bug了。至于修正,则还得等一段时间。
说明:此程序的bug是经网友鑫指出的,同时,他还发现,网上不少的程序,都存在这个问题,比如这里:http://sd.csdn.net/a/20110506/297285.html的红黑树的flash演示版本,也存在此类的问题。已在原文下发表了以下评论:
很遗憾,经反复测试,红黑树的flash版本有问题(其它的暂还没发现问题):http://www.cs.usfca.edu/~galles/visualization/flash.html。
如依次往插入这个序列,15,1,9,2,0,12,16,7,11,13,17,14,然后再删除根节点9,严重的错误就出来了。上面的版本只是简单的一个步骤用7代替9,成为根节点,然后把7节点着为黑色。树却没有后续调整,完全不平衡。
特此,把问题指出来,希望,这个红黑树的错误flash版本不致误导更多的人,同时,问题是朋友鑫提出的)。
我会记住这个问题,如果解决了,再发布在博客里。
后续:鑫指出:avl树也有问题。
July、结构之法 算法之道 博主。
2011.05.07。
但事实是,果真如此么?请看下文2.1节的修正。
2.1、红黑树不要求严格平衡
修正:本程序没有任何问题。有一点非常之重要,之前就是因为未意识到而造成上述错觉,即:红黑树并非严格意义上的二叉查找树,它只要满足它本身的五点性质即可,不要求严格平衡。所以,上面的例子中,12,1,9,0,2,11,7,然后删除根结点9,只要着色适当,同样不违反红黑树的五点性质。所以,结论是,我庸人自扰了,sorry。
还是这句话,有任何问题,欢迎任何人提出或指正。
第三部分、读者反馈
关于RB_Tree插入删除操作的讨论
July:
你好!关于RB_Tree的完整实现代码,你已经在你的博客中写出了。但我认为,你的代码中有需要改正的地方。
起 因
我这段时间正好在学习RB_Tree,由于我忽略了RB_Tree的性质(3):每个叶子结点都是黑色的,导致我对RB_Tree的操作纠结了好几天。在我还没意识到的时候,偶然间看到你的博客,想从中获得答案。然后就发现其中有值得商榷的地方。
错 误
下图是你写的插入修正函数InsertFixUp的部分截图:
你的文章地址:http://blog.csdn.net/v_july_v/article/details/6285620

图 1
正如《算法导论》所言,InsertFixUp 中每一次while循环都要面对3种情况:
case 1:z的叔叔y是红色的;
case 2:z的叔叔y是黑色的,且z是右孩子;
case 3:z的叔叔y是黑色的,且z是左孩子.
并且case 2是落在case 3内的,所以这两种情况不是相互排斥的!而在你的代码中,将case 2和case 3分别放在if和else中,导致它们相互独立。这是不对的。
修 正
所以,在图1中“标记①”处的else是不能加的,应将其删除。
遗憾的是,我认为你的RB_Tree的删除修正操作DeleteFixUp也出现了类似的错误:对于DeleteFixUp所处理的4种情况也同样不是相互排斥的,而你用一组if…else if…else if…将case 2, 3, 4全部独立开来。
以上便是鄙人的一点拙见,如果你认为有错误的地方,欢迎再讨论!
杨 超
CSDN ID: crisischaos
2011.10.06
考证:非常感谢杨兄来信指导。从算法导论一书原来的插入情况的修复伪代码来看:
//---------------------插入结点性质修复--------------------------------
//3种插入情况,都在下面的伪代码中(未涉及到所有全部的插入情况)。
/*
RB-INSERT-FIXUP(T, z)
1 while color[p[z]] = RED
2 do if p[z] = left[p[p[z]]]
3 then y ← right[p[p[z]]]
4 if color[y] = RED
5 then color[p[z]] ← BLACK ? Case 1
6 color[y] ← BLACK ? Case 1
7 color[p[p[z]]] ← RED ? Case 1
8 z ← p[p[z]] ? Case 1
9 else if z = right[p[z]]
10 then z ← p[z] ? Case 2
11 LEFT-ROTATE(T, z) ? Case 2
12 color[p[z]] ← BLACK ? Case 3
13 color[p[p[z]]] ← RED ? Case 3
14 RIGHT-ROTATE(T, p[p[z]]) ? Case 3
15 else (same as then clause with "right" and "left" exchanged)
16 color[root[T]] ← BLACK
*/
//然后的工作,就非常简单了,即把上述伪代码改写为下述的c++代码: ....确实如杨兄所说,理应如此(包括其后的对删除情况的修复)。日后,再做统一修改,再次谢谢。July、2011.10.06更新。
红黑树系列的前五篇文章:
完。

























 3939
3939

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










