模式识别之极大似然估计

引入

如果已知先验概率$p(w_i)$和类条件概率密度$p(x|w_i)$，则可以构造一个贝叶斯分类器
$p(w_i|x)=\frac{p(x|w_i)p(w_i)}{\sum\limits_{i=1}^{K} p(x|w_i)p(w_i)}$。

但是，在大多数实际问题中，生成数据的类条件概率密度分布（一般会假设为高斯分布等）的参数通常是未知的，因此，就需要有一些手段从样本数据中推断出这些参数。

这就产生了参数估计这一任务，即使用样本数据（训练数据）来估计未知的概率分布的参数。

参数估计方法分类

有监督的参数估计

己知概率分布的具体形式以及样本数据所属的类别；

无监督的参数估计

己知概率分布的具体形式，但是不知道样本数据所属的类别；

非参数估计

不知道概率分布的具体形式，但是己知样本数据所属的类别。

在有监督参数估计方法中，常用的两种方法：

极大似然估计

假定待估计的参数为某个固定值，估计准则为估计的参数使得样本集合的似然函数取最大值；

贝叶斯估计

假定待估计的参数为随机变量，估计准则为估计的参数使得平均风险达到最小值。

本文主要针对极大似然估计进行讲解。

问题

原问题

对于模式识别（分类）而言，假设共有$C$类且每一类的类条件概率密度分布都符合正态分布
$p(x|{{w}_{i}})\propto N({{\mu }_{i}},{{\sum }_{i}})$，
将带估计的参数矢量记为$\theta_i$，则
${{\theta }_{i}}=\left( \begin{matrix} {{\mu }_{i}}， {{\sum }_{i}} \end{matrix} \right)^T$ 。
为了强调类条件概率密度函数依赖于参数矢量，将其写为以下形式：
$p(x|{{w}_{i}},{{\theta }_{i}})$，
假定属于某个类别的训练样本只对本类别的参数估计提供信息，这样就能分别独立地考虑每个类别的参数估计。

子问题

己知样本集合$D={x_1,x_2,...,x_n}$，其中每一个样本都是独立地根据已知形式的概率密度函数$p(x|\theta)$抽取得到的，要求使用这些样本，估计概率密度函数中的参数矢量$\theta$的值。
由于假设样本间相互独立，故
$p(D|\theta )=\prod\limits_{k=1}^{n}{p({{x}_{k}}|\theta )}$。
又由于样本集$D$已知，故$p(D|\theta)$是关于$\theta$的函数，也称为样本集$D$下的似然函数。

参数$\theta$的极大似然估计是使$p(D|\theta)$达到最大的参数矢量$\hat{\theta }$。

极大似然

定义对数似然如下
$L(\theta )\triangleq \ln p(D|\theta )$，
此时问题转变为求取使对数似然函数$L(\theta )$达到最大的参数矢量
$\hat{\theta }=\arg \underset{\theta }{\mathop{\max }}\,L(\theta )$。

求解

令${{\theta }_{i}}={{({{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{p}})}^{T}}$且梯度算子${{\nabla }_{\theta }}$为
${{\nabla }_{\theta }}={{[\frac{\partial }{\partial {{\theta }_{1}}},\frac{\partial }{\partial {{\theta }_{2}}},...,\frac{\partial }{\partial {{\theta }_{p}}}]}^{T}}$，
对于
$L(\theta )\triangleq \ln p(D|\theta )=\sum\limits_{k=1}^{n}{\ln p({{x}_{k}}|\theta )}$
则
${{\nabla }_{\theta }}L=\sum\limits_{k=1}^{n}{{{\nabla }_{\theta }}\ln p({{x}_{k}}|\theta )}$。
因此，求解极大似然估计值的必要条件为方程组：
${{\nabla }_{\theta }}L=0$

示例

例1：假设训练样本符合多元正态分布，且协方差矩阵已知，需估计均值矢量。
极大似然估计目标
$L(\mu )\triangleq \ln p(D|\mu )=\ln \prod\limits_{k=1}^{n}{p({{x}_{k}}|\mu )}\text{=}\sum\limits_{k=1}^{n}{p({{x}_{k}}|\mu )}$
展开得：
$L(\mu)\text{=}\sum\limits_{k=1}^{n}{\left( -\frac{1}{2}\ln \left[ {{(2\pi )}^{d}}|\sum{|} \right]-\frac{1}{2}{{({{x}_{k}}-\mu )}^{T}}{{\sum }^{-1}}({{x}_{k}}-\mu ) \right)}$。
对目标函数求导等于0可得：
${{\nabla }_{\mu }}L=\sum\limits_{k=1}^{n}{{{\sum }^{-1}}({{x}_{k}}-\mu )=}0$
计算可得：
$\hat{\mu }=\frac{1}{n}\sum\limits_{k=1}^{n}{{{x}_{k}}}$
对正态分布均值的极大似然估计就是对全体样本取平均。

例2：对于均值和方差均未知的情况，考虑单变量情况，设$\theta=(\theta_1,\theta_2)^T=(\mu,\sigma^2)^T$。

极大似然估计目标
$L(\theta)\text{=}\sum\limits_{k=1}^{n}{\left( -\frac{1}{2}\ln {{(2\pi\theta_2 )}}-\frac{1}{2\theta_2}{{({{x}_{k}}-\theta_1 )}^{2}} \right)}$。
对目标函数求导等于0可得：
${{\nabla }_{\theta_2 }}L=\sum\limits_{k=1}^{n}{\frac{1}{\hat{\theta_2}}({{x}_{k}}-\theta_1 )=}0$
${{\nabla }_{\theta_1 }}L=-\sum\limits_{k=1}^{n}{\frac{1}{\hat{\theta_2}}+\sum\limits_{k=1}^{n}\frac{({{x}_{k}}-\hat{\theta_1 })^2}{\hat{\theta_2}^2}=}0$
计算可得：
$\hat{\mu }=\frac{1}{n}\sum\limits_{k=1}^{n}{{{x}_{k}}}$
${{\hat{\sigma }}^{2}}=\frac{1}{n}\sum\limits_{k=1}^{n}{{{({{x}_{k}}-\hat{\mu })}^{2}}}$
。
扩展可得，当正态分布为多元是，极大似然估计的结果为：
$\hat{\mu }=\frac{1}{n}\sum\limits_{k=1}^{n}{{{x}_{k}}}$
${{\hat{\sum }}}=\frac{1}{n}\sum\limits_{k=1}^{n}{{{({{x}_{k}}-\hat{\mu })}{({{x}_{k}}-\hat{\mu })}^T}}$

实现

% 本示例用于最大似然估计的教学示例
% 描述：1）生成过程：根据给定参数的正态分布生成二维数据点样本
% ······2）估计过程：根据最大似然估计算法估计参数值


% 设置随机数种子，使程序可重复
rng(10);

% 生成过程
NDATA = 1000; % 数据点数目
MU = [1,2]'; % 分布均值
COV = [0.5,0;0,0.8]'; % 协方差：假设各维度相互独立
SIGMA = diag(COV); % 方差：假设各维度相互独立
DATA = zeros(2,NDATA);
for k = 1 : NDATA
    % 依次生成数据
    DATA(:,k) = normrnd(MU,SIGMA);
end
disp('均值：');
disp(MU);
% disp('协方差：');
% disp(COV);
disp('方差：');
disp(SIGMA);

scatter(DATA(1,:),DATA(2,:)); % 绘制样本点
box on;

% 估计过程
MU_EST = mean(DATA,2); % 计算均值
DATA_DIF = bsxfun(@minus,DATA,MU_EST);
COV_SQUARE = zeros(2,2,NDATA);
for k = 1 : NDATA
    % 计算每个样本的协方差
    COV_SQUARE(:,:,k) = DATA_DIF(:,k)*DATA_DIF(:,k)';
end
COV_SQUARE_EST = mean(COV_SQUARE,3);
SIGMA_SQUARE_EST = diag(COV_SQUARE_EST);
disp('估计均值：');
disp(MU_EST);
% disp('估计协方差：');
% disp(sqrt(COV_SQUARE_EST));
disp('估计方差：');
disp(sqrt(SIGMA_SQUARE_EST));

% 注：系统自带的参数估计，假设数据各维度相互独立
[mu,s] = normfit(DATA');

运行上面的代码，可显示数据如下图：

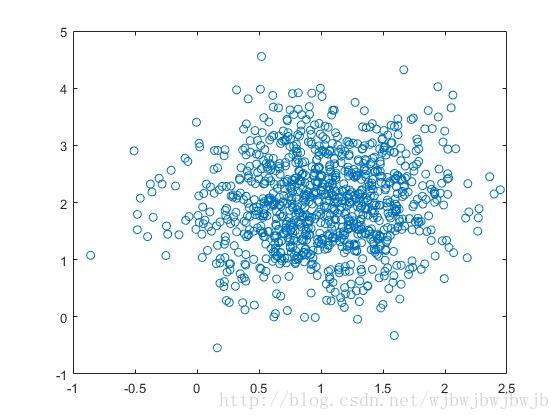
计算输出如下：

均值：
     1
     2

方差：
    0.5000
    0.8000

估计均值：
    1.0115
    1.9805

估计方差：
    0.5072
    0.7990