研究生课程系列文章参见索引《在信科的那些课》
基本原理
假定已给两个数据集P、Q, 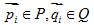 ,给出两个点集的空间变换f使他们能进行空间匹配。这里的问题是,f为一未知函数,而且两点集中的点数不一定相同。解决这个问题使用的最多的方法是迭代最近点法(Iterative Closest Points Algorithm)。
,给出两个点集的空间变换f使他们能进行空间匹配。这里的问题是,f为一未知函数,而且两点集中的点数不一定相同。解决这个问题使用的最多的方法是迭代最近点法(Iterative Closest Points Algorithm)。
基本思想是:根据某种几何特性对数据进行匹配,并设这些匹配点为假想的对应点,然后根据这种对应关系求解运动参数。再利用这些运动参数对数据进行变换。并利用同一几何特征,确定新的对应关系,重复上述过程。
迭代最近点法目标函数
三维空间中两个3D点,
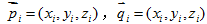 ,他们的欧式距离表示为:
,他们的欧式距离表示为:
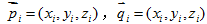 ,他们的欧式距离表示为:
,他们的欧式距离表示为:
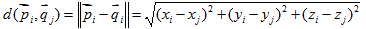
三维点云匹配问题的目的是找到P和Q变化的矩阵R和T,对于
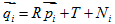 ,
,
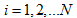 ,利用最小二乘法求解最优解使:
,利用最小二乘法求解最优解使:
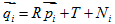 ,
,
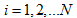 ,利用最小二乘法求解最优解使:
,利用最小二乘法求解最优解使:
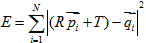
最小时的R和T。
数据预处理
实验中采集了五个面的点如下所示:








 本文介绍了3D空间中的迭代最近点算法(Iterative Closest Points, ICP)的基本原理和实现步骤,包括数据预处理、运动参数(旋转和平移)的计算,以及如何通过迭代优化匹配点的对应关系来求解空间变换。"
113009602,10494343,Java版Mc模组开发:环境搭建常见问题与解决方案,"['Java开发', 'Minecraft模组', '开发环境', 'Forge', 'IDE']
本文介绍了3D空间中的迭代最近点算法(Iterative Closest Points, ICP)的基本原理和实现步骤,包括数据预处理、运动参数(旋转和平移)的计算,以及如何通过迭代优化匹配点的对应关系来求解空间变换。"
113009602,10494343,Java版Mc模组开发:环境搭建常见问题与解决方案,"['Java开发', 'Minecraft模组', '开发环境', 'Forge', 'IDE']
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 518
518

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








