三维重建之点云配准：ICP(Iterative Closest Point) 算法及其变体

DtxGogogo

已于 2022-09-02 22:23:52 修改

阅读量3.2k

点赞数 6

分类专栏： Computer Graphics 文章标签：学习

于 2022-09-02 22:15:59 首次发布

原文链接：https://www.robots.ox.ac.uk/~avsegal/resources/papers/Generalized_ICP.pdf

版权

Computer Graphics 专栏收录该内容

5 篇文章 1 订阅

订阅专栏

1. 点云配准

点云配准（Point Cloud Registration）算法指的是输入两幅点云 Ps (source) 和 Pt (target)，输出一个变换T（假设只考虑刚性变换，即旋转R和平移t）使得 T(Ps)和Pt的重合程度尽可能高。

点云配准首先要知道两组点云的匹配关系，对于视觉三维点来说，可以通过视觉特征匹配来获取，对于雷达点云，可以通过最近邻匹配来获取。

假设我们现在知道点云的匹配关系后，通过粗配准（Coarse Registration）和精配准（Fine Registration）两步来计算变换矩阵。

粗配准指的是在两幅点云之间的变换完全未知的情况下进行较为粗糙的配准，目的主要是为精配准提供较好的变换初值；
精配准则是给定一个初始变换，进一步优化得到更精确的变换。
其中，粗配准存在解析解，精配准通过非线性优化的方式进一步优化结果。

2. ICP算法概述

点云匹配用公式来写就是：

$R^{*}, t^{*}=\underset{R, t}{\operatorname{argmin}} \frac{1}{P_{s}} \sum_{i=1}^{\left|P_{s}\right|}\left\|p_{t}^{i}-\left(R \cdot p_{s}^{i}+t\right)\right\|^{2}$

其中 $p^{i}_{s}$ 和 $p^{i}_{t}$ 是原点云 $P_{s}$ (source)和目标点云 $P_{t}$ （target）中的对应点。

ICP算法的思想如下：

如果我们知道两幅点云上点的对应关系，那么我们可以用 Least Squares 来求解刚性变换 T 中的 R , t 参数；
怎么知道点的对应关系呢？如果我们已经知道了一个大概靠谱的R , t参数，那么我们可以通过贪心的方式找两幅点云上点的对应关系（直接找距离最近的点作为对应点）。

ICP 算法实际上就是交替进行上述两个步骤，迭代进行计算，直到收敛。

因此可以给出ICP算法的一般处理流程：

1）点云预处理

滤波（去除一定范围之外的点，去除地面）、清理数据（去除nan值）等

2）匹配

应用上一步求解出的变换，找最近点（之前最好先做好粗配准，ICP对初值的要求比较高）

3）加权

调整一些对应点对的权重

4）剔除不合理的对应点对

5）计算 loss

6）最小化 loss，求解当前最优变换

7）回到步骤 2. 进行迭代，直到收敛

整体上来看，ICP 把点云配准问题拆分成了两个子问题：

找最近点
找最优变换

2.1 找最近对应点（Find Closet Point）

利用粗配准得到 $R_{0}$ 、 $t_{0}$ 或者上次得代得到的 $R_{k-1}$ 、 $t_{k-1}$ 对初始点云进行变换，得到一个临时的变换点云，然后用这个点云和目标点云进行比较，找出源点云中每一个点在目标点云中的最近邻点。

如果直接进行比较找最近邻点，需要进行两重循环，计算复杂度为 O(|Ps|⋅|Pt|) ，这一步会比较耗时，常见的加速方法有：

设置距离阈值，当点与点距离小于一定阈值就认为找到了对应点，不用遍历完整个点集；
使用 ANN(Approximate Nearest Neighbor) 加速查找，常用的有 KD-tree；KD-tree 建树的计算复杂度为 O(Nlog(N)) ,查找通常复杂度为 O(log(N)) (最坏情况下 O(N) )。

2.2 求解最优变换（Find Best Transform）

对于 point-to-point ICP 问题，求最优变换是有闭形式解（closed-form solution）的，可以借助 SVD 分解来计算。

在已知点的对应关系的情况下，设 $\bar{p}_{s}$ 和 $\bar{p}_{t}$ 分别表示源点云和目标点云的质心，令 $\hat{p}_{s}=p^{i}_{s}-\bar{p}_{s}$ ， $\hat{p}_{t}=p^{i}_{t}-\bar{p}_{t}$ ，令 $H=\sum_{i=1}^{\left|P_{s}\right|} {\hat{p}_{s}^{i} \hat{p}_{t}^{i}}^{T}$ ，这是一个3×3的矩阵，对H进行SVD分解得到 $H=U \Sigma V^{T}$ ，则point-to-point ICP问题的闭形式解如下：

最优旋转为：

$\large R^{*}=V U^{T}$

最优平移为：

$\large t^{*}=\bar{p}_{t}-R^{*} \bar{p}_{s}$

其具体的证明过程如下：

1）计算最优平移

2）计算最优旋转

3. ICP算法优缺点以及改进

优点

简单，不必对点云进行分割和特征提取
初值较好情况下，精度和收敛性都不错

缺点

找最近对应点的计算开销较大
只考虑了点与点距离，缺少对点云结构信息的利用

原始的 ICP 算法计算开销大，对初始变换敏感，容易陷入局部最优解。自 ICP 提出以来，有相当多的 ICP 改进算法，主要有：

3.1 Point-to-Line ICP

顾名思义，这种方式使用源点云到目标点云直线的距离度量来估计变换。主要区别在于误差函数的构建上。

ICP是找最近邻的一点，以点与点之间的距离作为误差，
而PLICP是找到最近邻的两点，两点连线，是以点到线的距离作为误差，

实际上，后者的误差度量方式更符合结构化场景中的雷达点云的实际情况。因此具有更小的误差。然而，它对非常大的初始位移误差的鲁棒性较差，因此需要比较精确的初始值。点到线的误差函数可以写为

3.2 Point-to-Plane ICP

原始 ICP 算法的代价函数中使用的 point-to-point 距离，point-to-plane 则是考虑源顶点到目标顶点所在面的距离，比起直接计算点到点距离，考虑了点云的局部结构，精度更高，不容易陷入局部最优。

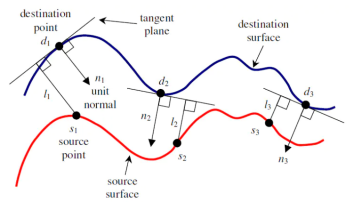
最小化损失函数可以写为：

其中 $\large n_{s}$ 是 $\large p_{t}$ 处的单位法线向量

点到平面通常比点到点收敛得更快；迭代次数更少；点到平面在每次迭代中速度较慢，并且需要表面法线

3.3 Plane-to-Plane ICP

point-to-plane 只考虑目标点云局部结构， plane-to-plane 顾名思义就是也考虑源点云的局部结构，计算面到面的距离

3.4 Generalized Iterative Closest Point (GICP)

综合考虑 point-to-point、point-to-plane 和 plane-to-plane 策略，精度、鲁棒性都有所提高；to be continue

3.5 Normal Iterative Closest Point (NICP)

考虑法向量和局部曲率，更进一步利用了点云的局部结构信息，其论文中实验结果比 GICP 的性能更好。NICP 算法的特点在于，其在匹配两组点云时并非考虑匹配点云之间的欧氏距离，而是将点云曲面的局部特征作为点对匹配以及计算变换的准则。具体来说主要可以分为以下几部分：计算点云中每个点的特征，即其表面的的法向量（normal）和曲面曲率(curvature)，以标记每个点；根据点的距离和特征找两组点云中的匹配点对；利用最小二乘法最小化，最小化目标函数，以求解点云变换矩阵。此处目标函数包括点面投影和法向量旋转误差。

$\large \widetilde{\mathbf{p}}=\left(\begin{array}{ll} \mathbf{p}^{T} & \mathbf{n}^{T} \end{array}\right)^{T}$

$\large \tilde{\mathrm{p}}^{\prime}=\mathrm{T} \oplus \tilde{\mathrm{p}}=\left(\begin{array}{c} \mathbf{R} \mathrm{p}+\mathrm{t} \\ \mathbf{R} n \end{array}\right)$

则可以构造一个六维的误差函数：

$\large \mathbf{e}_{i j}(\mathbf{T})=\left(\tilde{\mathbf{p}}_{i}^{\mathrm{c}}-\mathbf{T} \oplus \tilde{\mathbf{p}}_{j}^{\mathrm{r}}\right)$

3.6 else tricks

from 《Efficient Variants of the ICP Algorithm》，to be continue

Selection of Points选点（降采样）

Matching Points点匹配

Weighting of Pairs点权重

Rejecting Pairs点对剔除

Error Metric and Minimization误差度量和最小化

DtxGogogo

关注

6
点赞
踩
40

收藏

觉得还不错? 一键收藏
0
评论
三维重建之点云配准：ICP(Iterative Closest Point) 算法及其变体

点云匹配用公式来写就是：其中和是原点云(source)和目标点云（target）中的对应点。如果我们知道两幅点云上点的对应关系，那么我们可以用 Least Squares 来求解刚性变换 T 中的 R , t 参数；怎么知道点的对应关系呢？如果我们已经知道了一个大概靠谱的R , t参数，那么我们可以通过贪心的方式找两幅点云上点的对应关系（直接找距离最近的点作为对应点）。ICP 算法实际上就是交替进行上述两个步骤，迭代进行计算，直到收敛。
复制链接

扫一扫