2 针孔相机模型
常见的相机标定中,使用的相机多为针孔相机(Pinhole camera),也就是大家熟知的小孔成像理论。将其中涉及的坐标系之间的相互转换抽离出来,即为针孔相机模型的核心。
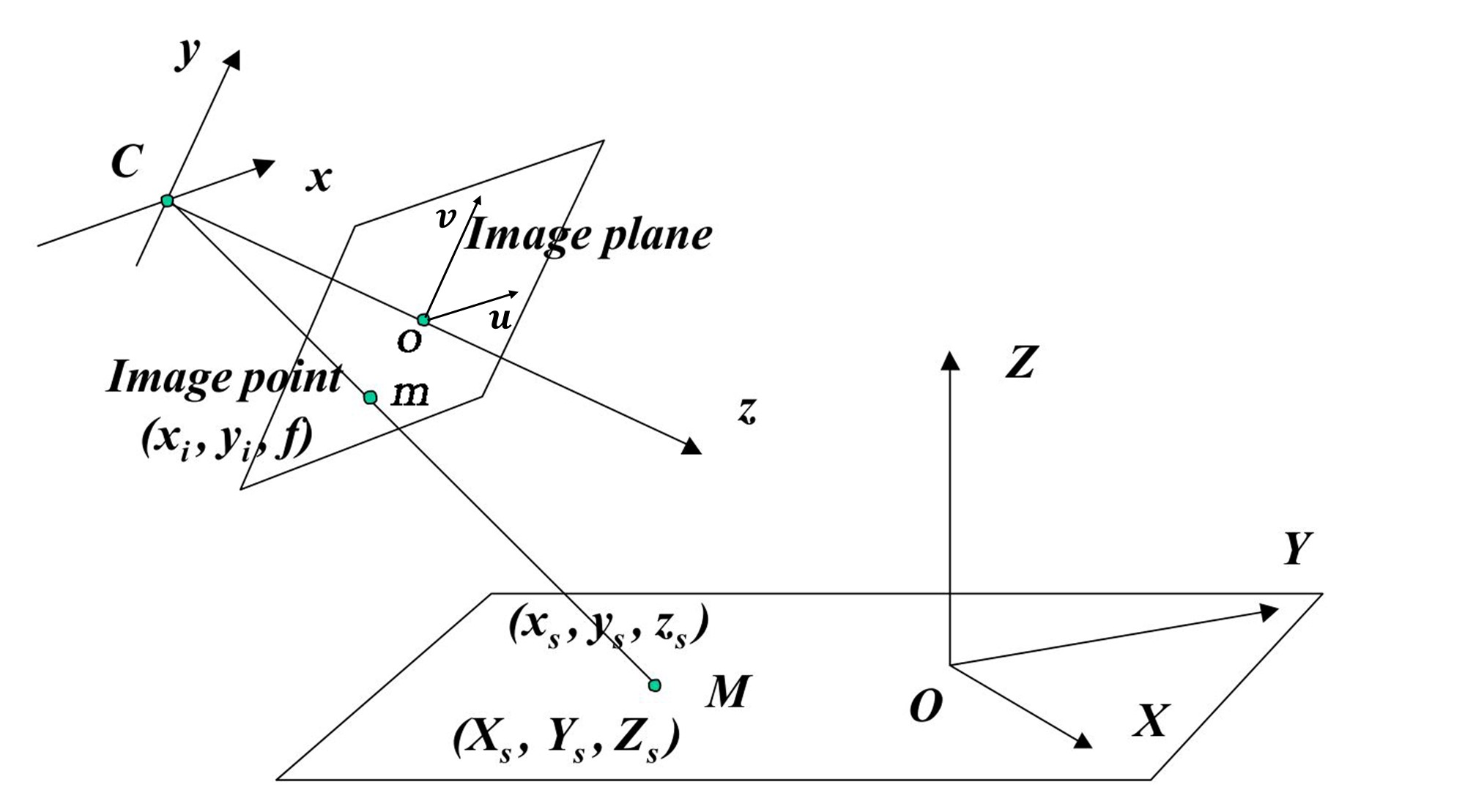
上图所示的模型即为针孔相机模型,当然现在有很多资料对其进行阐述,我这里挑选另一种便于理解的表达方法。这里为了方便阐述,将像平面和物方点置于光学中心的一侧(实际中光学中心位于像平面和物方点之间)。首先,让我们看一下其中的符号:
| 符号 | 含义 |
|---|---|
| C | 相机的光学中心(optical center)或者称为摄影中心 |
|
|
像主点(principal point),是指相机主光轴与像平面之间的交点,位于相片中心附近位置,用像素坐标表示为 [u0,v0]T ,用毫米单位表示时为 [x0,y0]T |
| f | 相机主距(focal length),或称相片主距 |
|
|
物方点,即被观测的三维点 |
| m | 物方点 M 在像平面上的像点,是光学中心
|
|
|
像平面坐标系,二维笛卡尔坐标系 |
| C−xyz | 像空间坐标系,三维笛卡尔坐标系,坐标轴 x,y 分别与像平面坐标系的 u,v 平行且具有相同的正方向,右手系 |
| O−XYZ | 物方空间坐标系,三维笛卡尔坐标系,定义具有随意性,右手系 |
| (xi,yi,f) | 像点 m 在像空间坐标系
|
| (xs,ys,zs) |





 本文介绍了相机标定中的核心概念——针孔相机模型,阐述了像点、物方点和光学中心的共线性,以及共线方程的矩阵形式。内容涵盖相机内外参数,包括相机的定向、定位参数(旋转和平移)和描述相机特性的参数(像素比例、像主点坐标等)。相机标定的目标是获取这些参数,以便进行三维到二维的转换。
本文介绍了相机标定中的核心概念——针孔相机模型,阐述了像点、物方点和光学中心的共线性,以及共线方程的矩阵形式。内容涵盖相机内外参数,包括相机的定向、定位参数(旋转和平移)和描述相机特性的参数(像素比例、像主点坐标等)。相机标定的目标是获取这些参数,以便进行三维到二维的转换。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1万+
1万+


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?







