Coding the Matrix： Week 4 The Basis 学习笔记

本周课程主要内容有：

1. 坐标系统（Coordinate System）；
2. 线性相关性；
3. 基底（Basis）与基底变换；
4. 交换定理；
5. 图像的投影表示。

先了解坐标系统与坐标表示（Coordinate representation）的基本概念：

• 向量空间 V 的坐标系统用 V 的生成器a1，a2，……，an表示；
• 向量空间 V 中的每个向量 v 都可以用线性组合的形式表示为 v = alpha1 * a1 + …… + alphan * an；
• 我们用参数组成的向量[alpha1，……，alphan] 表示向量 v ，称其为向量v 关于a1，……，an的坐标表示。

相关应用：如果图片向量可以通过坐标系统用坐标表示，那么能够实现图片存储与传送过程中的有损压缩（The lossy compression）。

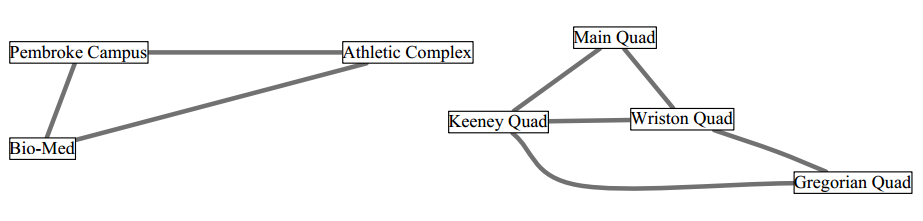
下面通过计算机图形学中的最小生成树（Minimum spanning forest）概念引出线性相关的知识。

通过上面的图中，首先介绍几个基本的概念：

节点（Node）：上图每个标签称为一个节点（用 xn 表示）。

边缘（Edge）：两个节点之间的连线。

图的控制集（The dominating set）：每个节点或者其相邻节点在图中的节点集。

路径（Path）：边缘序列 [{x1，x2}，{x2，x3}，……，{x(k-1)，xk}] 称为从 x1 到 xk 的路径。 

回环（Cycle）：从 x 到 x 的路径。

图生成集：对于图 G 中的每条边缘 [x，y] 都能在其中找到从 x 到 y 的路径的边缘集。

树（Forest）：不包含回环的边缘集。

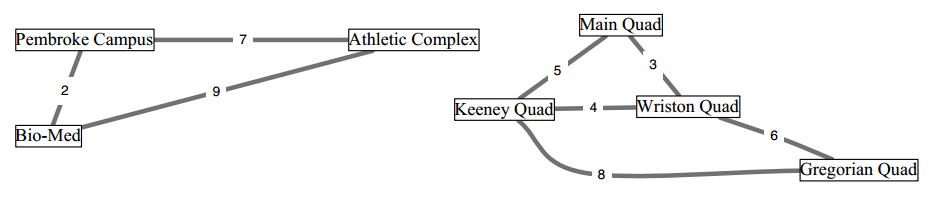
有了上面的概念基础，接下来提出最小生成树问题：

• 输入：一个图 G，并为其每条边缘赋予对应的实数权重。
• 输出：最小权重边缘集，该集合是生成树。

这个问题有两种解法，生长算法和收缩算法，算法描述如下：

关于图的一种向量表示如下：

对于一个含有 n 个节点的图 G 中的每条边缘，可以用一个 n 维向量表示，再把边缘连接的两个节点在向量中的对应位置一即可。

这样，上面的算法可以转换为对于向量的算法的研究，事实上，上面的两个算法是向量算法的特殊化表示而已。而向量的生长和收缩算法都需要判定一个向量在生成向量空间中是否是冗余的，所以需要一个冗余判据，这就是冗余向量引理（Superfluous-Vector Lemma）：如果一个属于集合 S 的向量v 可以表示为该集合的其他向量的线性组合形式，那么 Span（S - {v}） = Span S。

根据该引理，可以引出线性代数中的两个至关重要的概念：线性相关（linear dependency）与线性无关（linear independency）。

线性相关的定义为：对于向量v1，……，vn，如果零向量可以表示为这些向量的非平凡线性组合形式，那么称这些向量是线性相关的。

把线性相关知识与前面的知识联系起来，可以发现如下关系：

问题：如何判定一组向量v1，……，vn是线性相关的？

等同于

问题：如何判定一个矩阵的零空间是平凡的？

等同于

问题：如何判定一组齐次线性方程的解是平凡的？

等同于

问题：如何判定线性方程的一个解u1 是唯一解？

也就是说上面的四个问题都可以归结为一个计算问题——判定线性相关性：

• 输入：向量表 [v1，……，vn]。
• 输出：这组向量是否是相关的。

稍后我们再介绍解决这个计算问题的算法。

有了线性相关的基本知识，下面列出生长和收缩算法的向量描述：

关于这两个算法，通过前面的冗余向量引理，可以得出两个推论：

1. 生长算法推论：由生长算法得到的向量是线性不相关的。
2. 收缩算法推论：由收缩算法得到的向量是线性不相关的。

所以，如果这两个算法都可以顺利运行完成的话，那么可以得到一组向量，他们生成了向量空间 V ，并且是线性不相关的，这组向量就是向量空间 V 的基底。

也就是说，如果一个集合 S 满足下面两个条件，那么他是向量空间 V 的基底：

1. Span S = V；
2. S 是线性不相关的。

基底是线性代数中最重要的定义。

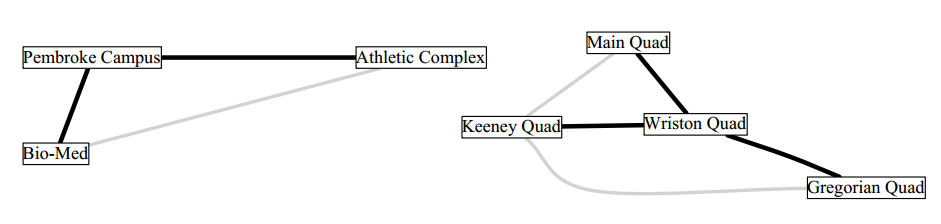
用前面的图举一个例子。

上图中的黑色线构成的边缘集 S （这个边缘集是图 G 生成树）是图 G 的一个基底，因为：

• Spanning：对于 G 中的每一条边缘 xy，都可以从 S 中找到从 x 到 y 的路径；
• Independent：S 中不存在回环。

接下来，我们可能想知道：是不是每一个向量空间都存在基底呢？

生长算法和收缩算法均可以提供证明这一问题答案的方法，但是要顺利完成证明，各自又存在一个尚未解决的问题：

• 生长算法：是否一定能够运行完成（terminate）？
• 收缩算法：每个向量空间是否都能由有限的向量集生成？

我们回顾一下前面的知识，一个向量空间 V 可以通过两种方法指定：

1. 指定 V 的生成器；
2. 齐次线性系统的解集。

由此可以得到两个基本的计算问题：

这两个问题留给读者自己思考解决。

下面，我们将线性相关与基底知识与前面介绍的坐标系统联系起来。

对于向量空间中的任何一个向量，我们如何确定其在坐标系统中有唯一的坐标表示？答案是生成器a1，a2，……，an是向量空间的一组基底。

唯一表示引理（Unique-Representation Lemma）：令 a1，a2，……，an 为向量空间 V 的一组基底，则对于每一个属于 V 的向量 v ，那么向量 v 用这组基底向量表示方式是唯一的。

向量空间的基底并不是唯一的，有时候，对于同一个向量，我们希望对其坐标表示在不同的基底下进行变换，由此引出另一个问题：基底变换（Change of basis）。

关于基底变换，有下面定理：

基底变换在图像处理中有一个典型的应用：角度移除（Removing perspective）。关于这一应用的详细介绍我们容后再说。

下面，我们再谈谈交换引理（Exchange Lemma）的相关内容。

交换定理可以用来解决这样的问题：

• 你有一个向量集合 S ；
• 你有一个向量 z ，并且想把它插入到 S ；
• 你希望保持集合 S 的大小不变，所以需要从 S 中去除一个向量 w；
• 你希望 Span S 不变。

先介绍简化版的交换引理：

通过这个引理，我们可以得到实现插入一个向量的方法，但是如果我们希望插入多个向量时，就会碰到一个问题：在插入后面向量的时候却去除了前面插入进去的向量。

所以，我们需要加强一下这个引理，以保护原有集合 S 中的某些元素以免被删除，根据这一需求得到了完整版的交换引理：

利用这个定理可以证明最小生成树的生长算法的正确性，有兴趣的读者可以自己试一试。

至此，本周的所有线性代数理论知识已经介绍完毕。

最后附上一些重要算法的伪代码描述：

算法一：判断一个向量是否是冗余的。

## Tell whether a vector in the list is superfluous.  
def is_superfluous(L, i):  
    ''''' 
    Input: 
        - L: list of vectors as instances of Vec class 
        - i: integer in range(len(L)) 
    Output: 
        True if the span of the vectors of L is the same 
        as the span of the vectors of L, excluding L[i]. 
 
        False otherwise. 
    '''
    # if the length of L is one
        # return False
    # Save  the ith element of L in b
    # Copy L to a new list B
    # Remove the ith element of B
    # Solve the equation B * x = b
    # if x is nontribial
        # return True
    # else
        # return False 

算法二：判断一组向量是否是线性不相关的。

def is_independent(L):
    '''
    input: a list L of vectors (using vec class)
    output: True if the vectors form a linearly independent list.
    '''
    # for all the elements in L
        # if the element is superfluous
            # return False
    # return True