m,n 没有给出线性系统实际大小的真实信息,在我们上文的例子中有三行和四列,但是第三行仅仅是前两行的组合,在消元后得到了零行,它对奇次问题 Ax=0 没有影响。第四列同样是相关的,列空间减到了二维平面。
最重要的数是矩阵的秩
r
,在消元过程中得到主元的个数是引入了这个数。等价的,最终矩阵
本篇文章的目标就是就是和使用下面四个想法:
- 线性无关或相关
- 生成一个子空间
- 子空间的基(一组向量)
- 子空间的维度(一个数)
首先是定义线性无关。给定一组向量 v1,…,vk ,对于他们的组合 c1v1+c2v2+⋯+ckvk (这种组合叫平凡组合),当权值 ci=0 时明显结果就是零向量: 0v1+⋯+0vk=0 ,现在的问题是是否只有这一种方式得到零,如果是,那么这些向量就是无关的。
如果存在任何其他组合得出零,那么他们就是相关的。
5、假设 c1v1+⋯+ckvk=0 只有在 c1=⋯=ck=0 时成立,那么向量 v1,…,vk 是线性无关的。如果任何 c 不为零,那么这些向量是线性相关的。其中一个向量是其他向量的组合。
当所有向量从原点出发时,线性相关很容易在三维空间里可视化,如果两个向量在同一条线上,那么他们就是相关的,如果三个向量在同一个平面上,那么他们也是相关的。一般情况下随便选择三个向量,他们是线性无关的(不在一个平面上),四个向量在
例1:如果 v1 是零向量,那么集合是线性相关的,例如我们可以令 c1=3 而其他 ci=0 ;这是非平凡组合,并且得到了零。
例2:矩阵
是线性相关的,因为第二列是第一列的三倍,列组合的权值-3,1,0,0可以得到零。
行也是线性相关的,第三行是第二行的二倍减去第一行的五倍。
例3:下面三角矩阵的列是线性无关的:
寻找一个列组合使得:
我们发现
c1,c2,c3
只有全为零是才成立。首先从最后一个方程可以看出
c3=0
,那么接下来我们发现
c2=0
,然后
c1=0
。产生零向量的唯一组合是平凡组合,
A
的零空间只包含零向量
当矩阵
A
的零空间
同样有种方法来推断
A
的行是无关的,假设
从第一元素我们发现 3c1=0 orc1=0 ,那么第二个元素得到 c2=0 ,最后 c3=0 。
任何阶梯矩阵
U
的非零行一定是无关的,更进一步,如果我们选取主元所在的列,他们也是线性无关的,在上文的例子中
主元列1和列3是无关的,不存在第三无关的列,自然更不会有第四个。列1和列4 也是无关的,但是如果最后一列的1变成0他们就是相关的。主元所在的列保证他们一定是无关的,一般的规则是:
6、阶梯矩阵
U
和最简矩阵
例4:
n×n
单位矩阵的列是无关的:
这些列
e1,…,en
表示
R4
空间内坐标轴方向上的单位向量
R4 中许多四个向量的集合是无关的,这些 e 可能是最安全的。
为了确定任何集合
有种情况特别重要,有
7、对于
Rm
中
n
个向量的集合,如果
例5:
R2
中的三个列不可能无关:
为了找出得到零的列组合,我们求
Ac=0
:
如果我们将自由变量 c3 赋值1,那么回代得到 c2=−1,c1=1 ,根据这些权值,第一列减去第二列加上第三列的得到零。
生成子空间
现在我们定义一个向量集合生成一个空间是什么意思。 A 的列空间是由列生成的,他们的组合产生了整个空间:
8、如果向量空间
例6:向量
例7:
A
的列空间就是它的列生成的空间,行空间是它的行生成的,
来自单位矩阵的坐标向量 e1,…,en 生成 Rn 空间,每个向量 b=(b1,…,bn) 是这些列的组合,在这个例子中权值就是这些元素 bi 本身: b=b1e1+⋯+ bnen ,但是其他矩阵的列也生成 Rn 。
向量空间的基
为了确定
b
是否是列的组合,我们尝试求解
9、 V 的基是一个向量序列,他们具有两个性质:
- 向量是线性无关的
- 他们生成空间
V 组合的性质是线性代数的基本,这意味着空间中的每个向量都是基向量的组合,因为空间是有他们生成的。还意味着组合是唯一的:如果 v=a1v1+⋯+akvk,v=b1v1+⋯+bkvk ,那么他们相减为零 0=Σ(ai−bi)bi ,现在无关表现为每个系数 ai−b−i 必须是零,因此 ai=bi 。对于 v 有且只有一种基向量的组合。
线性代数中有些东西是唯一的,但有些不是,如一个向量空间有无限个不同的基。只有方阵是可逆的,那么它的列就是无关的,他们是
Rn 的一个基,如下面这个非奇异矩阵的两列就是 R2 的一个基:
A=[1213]每个二维向量都是这些列的一个组合。
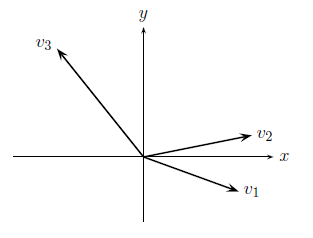
例8:图1中的 x−y 平面就是 R2 ,向量 v1 是线性无关的,但是它不能生成 R2 。三个向量 v1,v2,v3 肯定能生成 R2 ,但是他们是相关的。任何两个向量如 v1,v2 有两个性质——他们无关且生成空间,所以他们形成一个基,再次强调一下向量空间的基不是唯一的。
图1
例9:四个列生成 U 的列空间,但是他们是相关的:
U=⎡⎣⎢100300330210⎤⎦⎥ 有许多可能的基,但是我们给一个特殊的选择:包含主元的列(本例中是1,3列)作为列空间的一个基。这些列是无关的,而且很容易看出他们生成了空间。事实上, U 的列空间仅仅是
R3 中的 x−y 平面, C(U) 和 C(A) 的列空间不一样——但是无关列的数目是一样的。总结:任何矩阵列生成它的列空间。如果我们是无关的,那么列空间是他们的一个基——无论矩阵是方阵还是长方形矩阵。如果我们要求作为基的列生成整个空间 Rn ,那么矩阵是可以的方阵。
向量空间的维度
一个空间由无限多个不同的基,但是有些东西是他们共有的,基向量的数目是空间本身的一种性质:
10、一个向量空间 V 的任何两个基包含的向量个数一样,这个数是所有基共享的,表达了空间自由度的个数,也就是
V 的维度。我们必须证明这个事实:所有可能的基包含的向量数一样。图1中的 x−y 平面每个基中有两个平面;它的维度为2。在三维空间里我们有三个向量,他们分别沿 x−y−z 轴。空间 Rn 的维度是 n ,
U 的列空间维度为2;它是 R3 的子空间。零矩阵非常特殊,因为它的列空间只有零向量,空间是这个空间的基,所以维度为零。这里我们给出线性代数里最大的一个定理:
11、如果 v1,…,vm,w1,…,wn 都是同一个向量空间的基,那么 m=n ,向量的个数是一样的。
证明:假设 w 比
v 多(n>m),那么我们将产生一个矛盾,因为 v 形成一个基,他们必须生成一个空间,每个w 可以写成 v 的一个组合:如果w1=a11v1+⋯+am1vm ,这是矩阵 VA 的第一列:
W=[w1w2⋯wn]=[v1vm]⎡⎣⎢⎢a11⋮am1⎤⎦⎥⎥=VA我们不知道每个 aij ,但是我们知道 A 的大小(
m×n ),第二个向量 w2 也是 v 的一个组合,这个组合系数放到A 的第二列。因为 A 矩阵n>m ,所以 Ax=0 有非零解,那么 VAx=0 也有非零解!这样的话 w 不能是一个基——所以n>m 不成立。如果 m>n ,我们交换一下 v,w 并重复上面的操作。避免矛盾的唯一方法是 m=n ,这就证明了 m=n ,重复一遍:一个空间的维度是基中向量的个数。
这个证明说明 Rm 中的 m+1 个向量肯定是相关的,事实上我们可以看出一般结论:对于 k 维的子空间,大于
k 的向量集合是相关的。有另一个对偶的定理,我们从一个小点的或大点的向量集合开始,用一个基结束:
12、 V 中任何线性无关的集合通过添加更多的向量可以扩展成一个基。
生成
V 的任何集合通过去掉一些向量可以减为一个基。这个观点说明基是一个最大无关集合,在没有丧失无关性的前提下它无法变得更大,同时它也是最小生成集合,如果变得小店它就无法生成空间。
大家必须注意维度有两种不同的使用方式。我们说四维向量,意味着向量在 R4 空间里,现在我们已经定义了四维子空间;例如 R6 (第一个和最后一个元素为零)空间里的向量集合,四维子空间的成员是像 (0,5,1,3,4,0) 这样的六维向量。
最后一点是关于线性代数的语言,我们从来没有用过矩阵的基或空间的秩或基的维度这些词汇,这些短语都是没有任何意义的,列空间的维度等于矩阵的秩,我们将在下篇文章中证明。
























 1366
1366

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








