现在让我们谈论分类问题。这就像逻辑回归一样,除了我们想预测的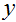
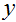
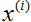
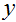
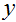
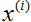
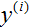
5 逻辑回归
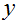 是离散值的事实,我们可以走进分类问题,使用我们老的线性回归算法在给定
是离散值的事实,我们可以走进分类问题,使用我们老的线性回归算法在给定
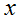 的情况下来预测
的情况下来预测
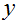 。然而,很简单构造这个方法工作很差的例子。直觉上,当我们知道
。然而,很简单构造这个方法工作很差的例子。直觉上,当我们知道
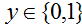 ,
,
 取大于1或者小于0的值,这个方法也没有意义。
取大于1或者小于0的值,这个方法也没有意义。
为了修正这个,让我们改变假设
 的形式。我们将会选择
的形式。我们将会选择
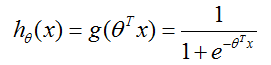
这里
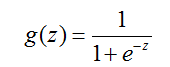
被称作逻辑函数或者Sigmoid函数。这里有一个
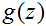 的图像:
的图像:
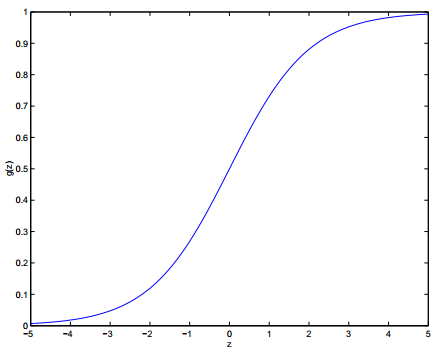
注意当
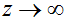 ,
,
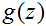 趋于1,当
趋于1,当
 ,
,
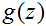 趋于0。而且,
趋于0。而且,
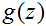 总是在0和1中间,因此
总是在0和1中间,因此
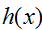 也是。就像以前,我们仍旧保持让
也是。就像以前,我们仍旧保持让
 的惯例,以致
的惯例,以致
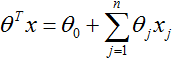 。
。
现在,让我们选择
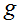 为(上面)给定的。其他的从0到1平湖增长的函数也可以使用,但是由于几个原因,这几个原因我们只会看到(当我们讨论GLMS和当我们讨论生成学习算法时),这个逻辑函数的选择是相当自然的一个。在继续讲之前,这里有一个关于sigmoid函数导数的有用的特征,我们把导数写作
为(上面)给定的。其他的从0到1平湖增长的函数也可以使用,但是由于几个原因,这几个原因我们只会看到(当我们讨论GLMS和当我们讨论生成学习算法时),这个逻辑函数的选择是相当自然的一个。在继续讲之前,这里有一个关于sigmoid函数导数的有用的特征,我们把导数写作
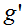 :
:
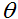 ?接下来我们看到最小二乘回归如何在一组假设下作为最大似然估计量可以被推出,让我们赋予我们的分类模型一组概率假设,然后通过最大似然来选择合适的参数。
?接下来我们看到最小二乘回归如何在一组假设下作为最大似然估计量可以被推出,让我们赋予我们的分类模型一组概率假设,然后通过最大似然来选择合适的参数。
让我们假设
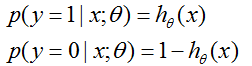
注意到,这可以更简洁的被写作
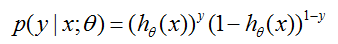
假设m个训练样例是独立生成的,我们可以写出参数的似然为
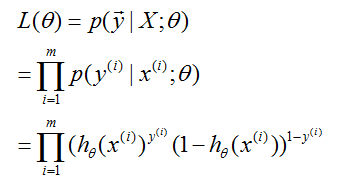
就像以前,最大化log似然更简单一些:
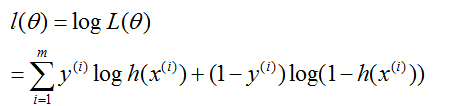
我们如何最大化似然?和在线性回归情况的推导相似,我们可以使用梯度上升。以向量符号写出,因此我们的更新(规则)为
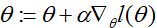 。(注意在更新规则中为正号而不是负号,因为我们现在正在最大化一个函数,而不是最小化)。让我们首先从仅仅一个训练样例
。(注意在更新规则中为正号而不是负号,因为我们现在正在最大化一个函数,而不是最小化)。让我们首先从仅仅一个训练样例
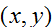 开始,取导数得到随机梯度上升规则:
开始,取导数得到随机梯度上升规则:
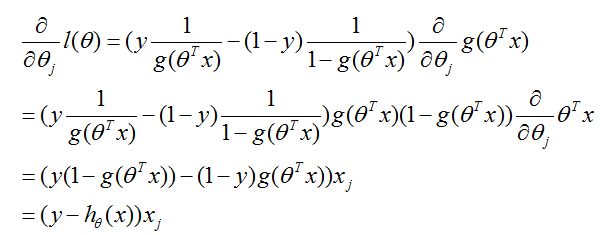
上面,我们使用了
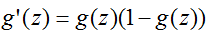 这一事实。因此,我们的梯度上升规则为
这一事实。因此,我们的梯度上升规则为
如果我们把它和LMS更新规则进行比较,我们可以看出它看起来是相同的;但是这不是相同的算法,因为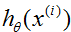
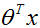
6 离题:感知器学习算法
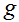 的定义为阈值函数是自然的:
的定义为阈值函数是自然的:
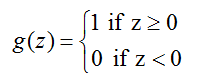
然后如果我们像以前令
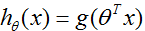 但使用这个修正的
但使用这个修正的
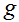 ,而且使用更新规则
,而且使用更新规则
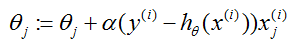
然后我们得到感知器学习算法。
在20世纪60年代,这个“感知器”被认为是一个关于单个神经元如何在大脑工作
的粗糙模型。鉴于这个算法是多么简单,之后在这门课当我们谈论学习理论时,它也会我们分析提供一个开端。然而要注意的是,尽管感知器算法外观上和我们之前讨论过的算法相似,实际上它是一个和逻辑回归和最小二乘线性回归类型非常不同的算法;尤其是,赋予感知器的预测有意义的概率解释或作为一个最大似然估计估计算法得到感知器是困难的。
7 最大化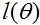
回到逻辑回归,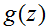
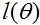
我们开始,让我们首先考虑牛顿法求得一个函数的零解。特有地,假定我们有某个函数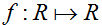
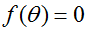
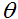
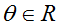
这个方法有一个自然的解释,在解释中我们把它看作通过一个线性函数来近似函数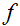
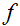
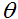
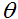
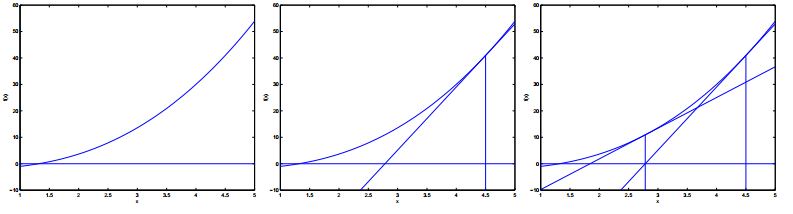
这里有一幅运行牛顿法的图片:
在最左边的图形,我们看到画出了函数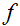
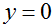
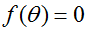
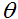
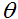
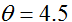
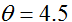
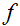
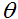
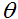
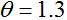
牛顿法给出了一种求解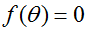
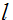
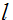
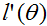
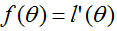
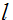
(一些需要思考的地方:如果我们想牛顿法最小化而不是最大化一个函数,这个如何改变?)
最后,在我们的逻辑回归环境下,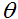
给出。这里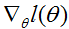
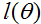
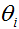
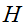
牛顿法通常比(批)梯度下降收敛的更快,需要少很多次的迭代来接近最小值。不过,牛顿法的一次迭代比梯度下降的一次迭代代价更高,因为它需要求出一个n x n的Hessian阵和它的逆;但是只要n不是太大,牛顿法通常在整体上快很多。当牛顿法被用来最大化逻辑回归log似然函数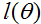
想写一写机器学习的翻译来巩固一下自己的知识,同时给需要的朋友们提供参考,鉴于作者水平有限,翻译不对或不恰当的地方,欢迎指正和建议。








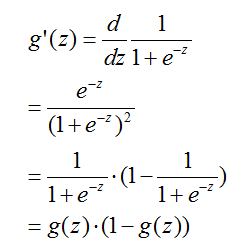

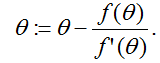
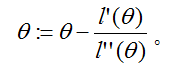
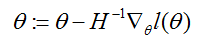
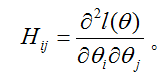














 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








