离散数学及应用 -- 02 基本结构：集合、函数、序列、求和与矩阵

最新推荐文章于 2024-03-20 21:32:23 发布

--y--

最新推荐文章于 2024-03-20 21:32:23 发布

阅读量1.2k

点赞数

文章标签：学习

本文链接：https://blog.csdn.net/2201_75368933/article/details/130607770

版权

集合

集合是对象的一个无序的聚集，对象也称为集合的元素或成员。集合包含它的元素。

$a$ ∈A：a是集合A中一个元素

$a$ ∉A：a是集合A中一个元素

描述集合的方式：

花名册方法：在可能的情况下一一列出集合中的元素；有明显规律的就先列出集合的某些元素，然后用省略号代替。

集合构造器：通过描述作为集合的成员必须具备的性质来刻画集合中的那些元素

eg.O={x|x是小于10的正奇数}

$\mathbf{N}$ = {0,1,2,3...}	自然数集
$\boldsymbol{Z}$ = {...,-2,-1,0,1,2,...}	整数集
$\mathbf{Z^{+}}$ = {1,2,3,...}	正整数集
$\mathbf{Q}$ = {p/q \| p∈ $\mathbf{Z}$ ，q∈ $\mathbf{Z}$ ，且q≠0}	；有理数集
$\mathbf{R}$	实数集
$\mathbf{R^{+}}$	正实数集
$\mathbf{C}$	复数集

A和B是相同的集合：当且仅当A和B拥有相同的元素，即 $\forall x(x \in A \leftrightarrow x \in B)$

空集： $\varnothing$ 或者 { }表示，空集是一个特殊的不含任何元素的集合

单元素集：只有一个元素的集合

文氏图：全集+其他集合

子集： $A\subseteq B$ 当且仅当 $\forall x(x \in A\rightarrow x \in B)$

对于任意集合S，(i) $\varnothing \subseteq S$ , (ii) $S\subseteq S$

真子集： $A\subset B$ ，当且仅当集合A是集合B的子集但A≠B

即 $\forall x(x\in A\rightarrow x\in B) \wedge \exists x(x\in B\wedge x\notin A)$

证明集合A和B相等，就证明 $\mathbf{A\subseteq B}$ 和 $\mathbf{B\subseteq A}$

集合的大小：令S为集合。如果S中恰有n个不同元素(n为非负整数)，我们就说S是有限集，而n是S的基数。S的基数记为 | S |。

一个集合称为是无限的如果它不是有限的。

幂集 $P(S)$ ：给定集合S，S的幂集是集合S所有子集的集合。

如果一个集合有n个元素，那么它的幂集就有 $2^{n}$ 个元素

有序n元组： $a_{1},a_{2},...,a_{n}$ 是以 $a_{1}$ 为第1个元素， $a_{2}$ 为第2个元素 , ... , $a_{n}$ 为第n个元素的有序聚集

两个有序n元组是相等的当且仅当每一对对应的元素都相等。

有序二元组称为序偶。序偶(a,b)和(c,d)相等当且仅当 a=c 和 b=d。

笛卡儿积：令A和B为集合。笛卡儿积用 $A\times B$ 表示，是所有序偶 (a,b) 的集合，其中 a∈A 且 b∈B 。

$A\times B=\left \{ (a,b)|a\in A \wedge b\in B \right \}$

笛卡儿积的个数 = 集合A中元素个数 $\times$ 集合B中元素个数

笛卡儿积 $A\times B$ 和 $B\times A$ 并不相等，除非 $A=\varnothing$ 或 $B=\varnothing$ 或 $A\times B=\varnothing$ 或 $A=B$

集合 $A_{1},A_{2},...,A_{n}$ 的笛卡儿积用 $A_{1}\times A_{2}\times ...\times A_{n}$ 表示，是有序n元组( $a_{1}$ , $a_{2}$ , ... , $a_{n}$ )的集合，其中 $a_{i}$ 属于 $A_{i}$ , $i=1,2, ..,n$ 。

即 $A_{1}\times A_{2}\times ...\times A_{n}=\left \{ \left ( a_{1},a_{2},...,a_{n} \right ) | a_{i}\in A_{i},i=1,2,...,n \right \}$

集合A和自身的笛卡儿积： $A^{2}=A\times A$

$A^{3}=A\times A \times A$

$A^{n}=\left \{ \left ( a_{1},a_{2},...,a_{n} \right ) | a_{i}\in A_{i},i=1,2,...,n \right \}$

关系：笛卡儿积 $A\times B$ 的一个子集 R 称为是从集合A到集合B的一个关系。R的元素是序偶，其中第一个元素属于A而第二个元素属于B。

使用带量词的集合符号：

$\forall x\in S(P(x))$ 是 $\forall x(x\in S\rightarrow P(x))$ 的简写，表示P(x)在集合S所有元素上的全称量化

$\exists x\in S(P(x))$ 是 $\exists x(x\in S\wedge P(x))$ 的简写，表示P(x)在集合S所有元素上的存在量化

真值集：给定谓词P和论域D，定义P的真值集为D中使P(x)为真的元素x组成的集合。

P(x)的真值集记为 $\left \{ x\in D\; | \; P(x) \right \}$ 。

eg. 谓词P(x) 是 ''|x| = 1''，论域是整数集合。

这里P的真值集为{-1 , 1} 。

$\forall xP(x)$ 在论域 $U$ 上为真当且仅当P的真值集是集合 $U$ 。

$\exists xP(x)$ 在论域 $U$ 上为真当且仅当P的真值集非空。

集合运算

令A和B为集合：

$A\cup B = \left \{ x\; |x\in A\: \vee x\in B \right \}$

$A\cap B = \left \{ x\; |x\in A\: \wedge x\in B \right \}$

两个集合称为是不相交的，如果它们的交集为空集。

容斥原理（包含排斥原理）： $|A\cup B|=|A|+|B|-|A\cap B |$

差集： $A-B=\left \{ x\: |x\in A\wedge x\notin B \right \}$

补集： $\overline{A}=\left \{ x\in U\: |\: x\notin A \right \}$

集合恒等式：可以通过成员表（与真值表类似，0&1）或下列恒等式证明

扩展的并集和交集

一组集合的并集是包含那些至少是这组集合中一个集合成员的元素的集合

$A_{1}\cup A_{2}\cup ...\cup A_{n}=\bigcup_{i=1}^{n}A_{i}$

一组集合的交集是包含那些属于这组集合中所有成员集合的元素的集合

$A_{1}\cap A_{2}\cap ... \cap A_{n}=\bigcap_{i=1}^{n}A_{i}$

函数（映射、变换）

令A和B非空集合。从A到B的函数 f 是对元素的一种指派，对A的每个元素恰好指派B的一个元素。如果B中元素 b 是唯一由函数 f 指派给A中元素 a 的，则我们就写成 f(a)=b。如果 f 是从A到B的函数，就写成 f：A→B。

如果 f 是从A到B的函数（f 把A映射到B），则A是 f 的定义域，B是 f 的陪域。

如果 f(a)=b，则b是a的像，a是b的原像。

f 的值域或像是A中元素的所有像的集合。

陪域就是集合B的所有元素，而值域是被指派到的元素。

函数相等：当且仅当两个函数有相同的定义域、陪域，且定义域中的每个元素映射到陪域中相同的元素。

实值函数：函数其陪域是实数集合。

整数集函数：函数其陪域是整数集合。

具有相同定义域的两个实值函数或两个整数集函数可以相加和相乘。

令 $f_{1}$ 和 $f_{2}$ 是从A到R的函数，那么 $f_{1}+f_{2}$ 和 $f_{1}f_{2}$ 也是从A到R的函数。

$(f_{1}+f_{2})(x)=f_{1}(x)+f_{2}(x)$

$(f_{1}f_{2})(x)=f_{1}(x)f_{2}(x)$

令 f 为从A到B的函数，S为A的一个子集。S在函数 f 下的像是由S中元素的像组成的B 的子集。用 f(S)表示S的像，则 $f(S)=\left \{ t\, |\, \exists\, s\in S(t=f(s)) \right \}$

f(S)是一个集合

令A={a,b,c,d,e}，而B={1,2,3,4}，且 f(a)=2, f(b)=1, f(c)=4, f(d)=1及f(e)=1。子集S={b,c,d}的像是集合 f(S)={1,4}

一对一函数（单射函数）：这种函数不会把同样的值赋给定义域中两个不同元素。

即 $\forall a\forall b(f(a)=f(b)\rightarrow a=b)$

或 $\forall a\forall b(a\neq b \rightarrow f(a)\neq f(b) )$

在定义域内:

递增	当 $x<y$ 时，有 $f(x)\leq f(y)$
严格递增	当 $x<y$ 时，有 $f(x)<f(y)$
递减	当 $x<y$ 时，有 $f(x)\geq f(y)$
严格递减	当 $x<y$ 时，有 $f(x)>f(y)$

映上函数（满射函数）：函数值域与陪域相等，即陪域中每个成员都是定义域中某个元素的像

即当且仅当对每个 $b\subseteq B$ 有元素 $a\subseteq A$ 使得 $f(a)=b$

或 $\forall y\exists x(f(x)=y)$

双射函数：函数既是一对一的又是映上的

如果 f 时从集合A到自身的函数。如果A是有限的，那么 f 是一对一的当且仅当它是映上的。

假设 f：A→B

要证明 f 是单射的	证明对于任意 $x,y\in A$ ,如果 $f(x)=f(y)$ ,则 $x=y$
要证明 f 不是单射的	找到特定的 $x,y\in A$ ,使得 $x\neq y$ 且 $f(x)=f(y)$
要证明 f 是满射的	考虑任意元素 $y\in B$ ,并找到一个元素 $x\in A$ 使得 $f(x)=y$
要证明 f 不是满射的	找到一个特定的 $y\in B$ ,使得对于任意 $x\in A$ 有 $f(x)=y$

反函数：只有在函数 f 是一一对应的（既是一对一的，又是映上那个的），才能定义反函数

当 $f(a)=b$ 时，有 $f^{-1}(b)=a$

一一对应关系称为可逆的

不是一一对应关系，就称为不可逆的

函数的合成

令 g 为从集合A到集合B的函数，f 是从集合B到集合C的函数，函数 f 和 g 的合成，记作 $f\circ g$ 定义为 $a\in A$ ： $(f\circ g)(a)=f(g(a))$

$f\circ g$ 没有定义除非 $g$ 的值域是 $f$ 的定义域的子集

交换律对函数合成不成立： $f\circ g\neq g\circ f$

${\color{Red} (f^{-1})^{-1}=f}$

函数的图：令 f 是从集合A到集合B的函数，函数 f 的图像是序偶集合{(a,b) | a∈A 且 f(a)=b}

下取整函数：把X向下取到小于或等于x又最接近x的函数 ┕ $\frac{1}{2}$ ┙=0或 [ $\frac{1}{2}$ ]=0

上取整函数：把X向上取到大于或等于x又最接近x的函数 ┕ $\frac{1}{2}$ ┙=1

阶乘函数 $f:\mathbf{N\rightarrow Z^{+}}$ ，记为 $f(n)=n\, \mathbf{!}$

$n\, \mathbf{!}\sim \sqrt{2\pi n}(\frac{n}{e})^{n}$

部分函数：一个从集合A到集合B的部分函数 f 是给A的一个子集（成为 f 的定义域）中的每个元素a指派唯一的一个B中的元素b。集合A和B分别称 f 的域和陪域。f 对于A中但不在 f 的定义域中的元素无定义。当 f 的定义域等于A时，就说f是全函数。看集合&函数定义域

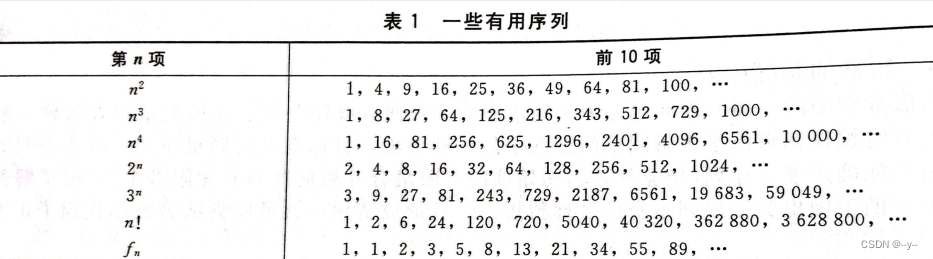
序列

序列是一个从整数集的一个子集{0,1,2,,...}或{1,2,3,...} 到一个集合S的函数。用记号 $a_{n}$ 表示整数n的像。称 $a_{n}$ 为序列的一个项。

几何级数： $a,ar,ar^{2},...,a^{n},...$ 初始项a和公比r都为实数

算术级数： $a,a+d,a+2d,...,a+nd,...$ 初始项a和公差d都为实数

递推关系：就类似于 $a_{n}=a_{n-1}+3$

斐波那契数列：初始条件 $f_{0}=0,f_{1}=1$

递推关系 $f_{n}=f_{n-1}+f_{n-2}\; \; \; \; n=2,3,4,...$

闭公式：当为序列的项找到一个显式公式（找到带初始条件的递推公式）

Lucas序列：初始条件 $L_{1}=1,L_{2}=3$

递推关系 $L_{n}=L_{n-1}+L_{n-2}$

求和

集合的基数

集合A和集合B有相同的基数，当且仅当存在从A到B的一个一一对应。当A和B有相同的基数时，就写成 $|\, A\, |=|\, B\, |$ 。

可数集：一个集合或者是有限集或者与自然数集具有相同的基数

有理数集合就是可数无限的

如果一个无限集S是可数的，写作 | S | =ℵ $_{0}$ （阿里夫零）

不可数集合：一个集合是不是可数，就称为不可数的

实数集是不可数的

可数集合的任意子集合都是可数的

任何含有不可数子集合的集合都是不可数的

如果 $A$ 和 $B$ 是可数集合，则 $A\cup B$ 也是可数集合

矩阵

0-1矩阵：所有元素非0即1.

布尔积：运算 $\vee$ 代替加法，运算 $\wedge$ 代替乘法

但实际就是两个矩阵的普通乘积

--y--

关注

0
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
离散数学及应用 -- 02 基本结构：集合、函数、序列、求和与矩阵

部分函数：一个从集合A到集合B的部分函数 f 是给A的一个子集（成为 f 的定义域）中的每个元素a指派唯一的一个B中的元素b。令A={a,b,c,d,e}，而B={1,2,3,4}，且 f(a)=2, f(b)=1, f(c)=4, f(d)=1及f(e)=1。令 f 为从A到B的函数，S为A的一个子集。函数的图：令 f 是从集合A到集合B的函数，函数 f 的图像是序偶集合{(a,b) | a∈A 且 f(a)=b}如果 f 是从A到B的函数（f 把A映射到B），则A是 f 的定义域，B是 f 的陪域。
复制链接

扫一扫