衍射:当光在传播中遇到狭缝与波长差不多的障碍物时,光传到障碍物的阴影区且形成明暗变化的光强分布。
夫琅禾费单缝衍射


明纹:
暗纹:
中央明纹宽度:
其他明纹宽度:
中央明纹会比其他明纹亮
光栅


光栅常量:, 其中,
为不透光的宽度,
为透光的宽度
光栅常量一般在的数量级
光栅的衍射条纹是衍射和干涉的总效果
光栅方程(明纹条件):
缺级:
偏振

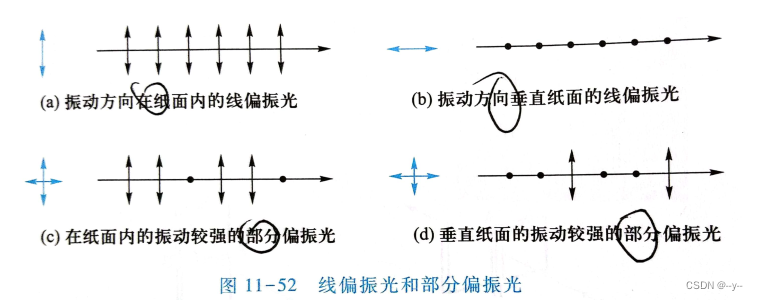
马吕斯定律

布儒斯特角:反射光为完全偏振光,折射光为部分偏振光
&







 文章讲述了光在遇到狭缝或类似障碍物时产生的衍射现象,特别是夫琅禾费单缝衍射中的明纹和暗纹分布。光栅的定义和其常量被提及,以及光栅常量通常的数值范围。光栅衍射条纹结合了衍射和干涉的效果,文章还讨论了光的偏振现象,包括马吕斯定律和布儒斯特角的应用。
文章讲述了光在遇到狭缝或类似障碍物时产生的衍射现象,特别是夫琅禾费单缝衍射中的明纹和暗纹分布。光栅的定义和其常量被提及,以及光栅常量通常的数值范围。光栅衍射条纹结合了衍射和干涉的效果,文章还讨论了光的偏振现象,包括马吕斯定律和布儒斯特角的应用。
















 1274
1274

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








