关键词:
孔径光阑、入射光瞳和出射光瞳、视场光阑、第一辅助光线、第二近轴光线、理想像高、F数、数值孔径、消杂光光阑、渐晕光阑、线性/几何渐晕系数、空间像、景深、以入射光瞳中心为坐标原点的物像位置关系公式、视差、透视距离D、物方/像方远心光路、放大镜的光束限制、显微镜系统的光束限制、望远镜系统的光束限制、照相物镜系统的光束限制
(本文章修缮于2024.12.1)
一、文章总览

二、光阑的作用
2.1为什么需要光阑

2.2横向尺寸、通光孔径和光阑
光学系统的横向尺寸:

通光孔径:

光阑:

2.3光阑的分类
①孔径光阑
定义及作用:

作用示意图:


当光位置改变时,应相应地改变其直径以保证轴上点的光束的孔径角不变。
同时:

作为目视观察用的光学系统,如放大镜、望远镜等系统,一定要把眼睛的瞳孔作为整个系统的个光阑来考虑。
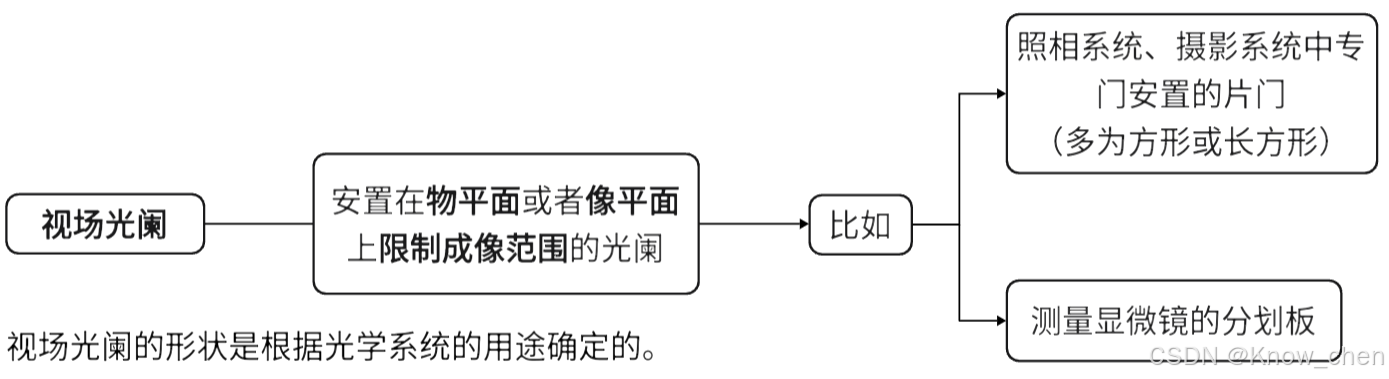
②视场光阑
定义及作用:
③渐晕光阑
渐晕的定义:
轴外光束被拦截的现象称为“渐晕”(是一种现象)

渐晕光阑多是透镜框
渐晕作用示意图:


渐晕光阑的优缺点:

④消杂光光阑
杂光的形成:

杂散光形成示意图:
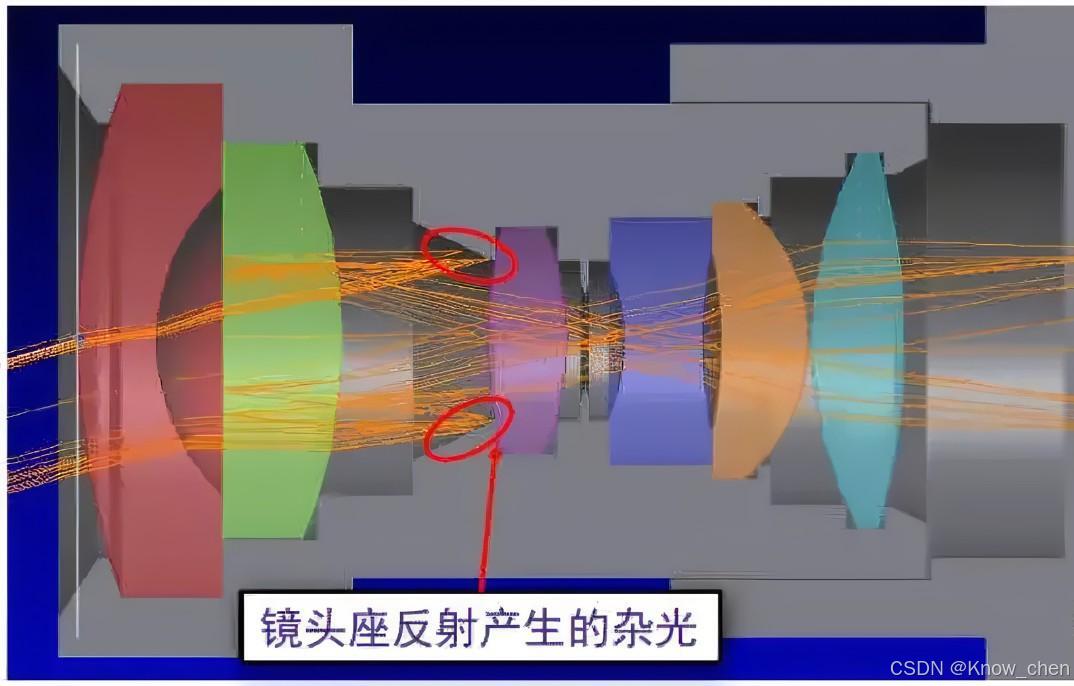
杂光的危害:

消杂光光阑:

消杂光光阑示意图:

三、光阑在光路计算中的作用
3.1为什么需要光阑?
光学零件的直径是有一定大小的,不可能让任意大的光束通过,而实际光学系统总是对一定孔径的光束成像。因此,必须有一个光孔(可能是一个透镜框,也可能是一个专门设置的光阑)限制着光束的大小。
孔径光阑就是这样的光孔,如下图Q1QQ2。

3.2孔径光阑、入射光瞳和出射光瞳
①物空间和像空间
为了方便理解后面的入射光瞳和出射光瞳的概念先介绍一下像空间和物空间的概念。
定义:
凡是物所在的空间(包括实物和虚物)称为物空间:像(包括实像和虚像)所在的空间称为像空间。
两个空间是无限扩展的,并不是由折射面或一个光学系统的左边和右边机械地分开的。
通俗来说:
它们两就像两平行世界一样,在同一个空间重叠在一起,因为虚的那一部分是不存在的,只是人为去规定的,所以不能机械地分开(没法实体去划分),无限扩展,两空间的范围都是从-无限到+无限,只是有虚实之分。下面详细说明:
物/像空间的分类:


物空间:
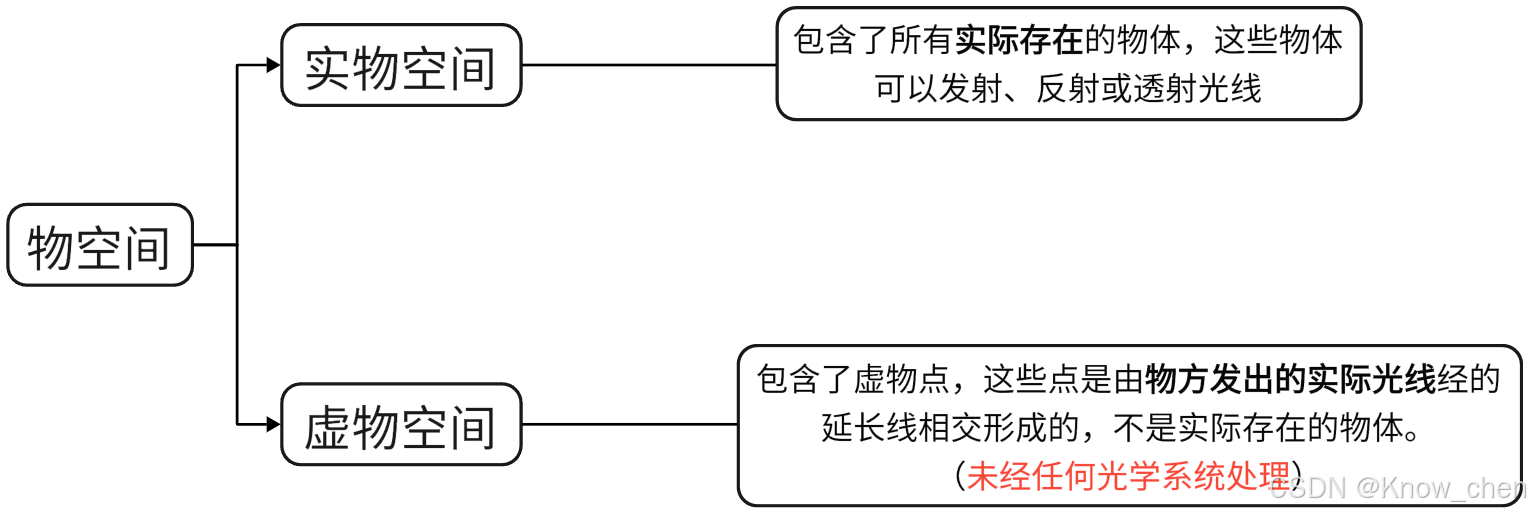

像空间:


②光瞳

出射光瞳的示意图:
红色光线形成出瞳
可以直观的看到入射光瞳是如何形成的。(是一个虚物)
孔径光阑通过前面的光学系统成像在(虚)物空间的物(虚物)。
注:
入瞳的形成可以理解为:虚物成实像,虚物是入瞳,实像是光阑。
这也就是为什么后面算入瞳--光阑之间的垂轴放大率β的时候是Da/D(Da为光阑直径),不是D/Da的原因了,因为某种程度上可以说是入瞳通过光学系统形成了光阑。

出射光瞳的示意图:
蓝色光线形成入瞳
可以直观的看到出射光瞳是如何形成的。(是一个虚像)
孔径光阑通过后面的光学系统成像在(虚)像空间的像(虚像)。

③入瞳与出瞳的共轭
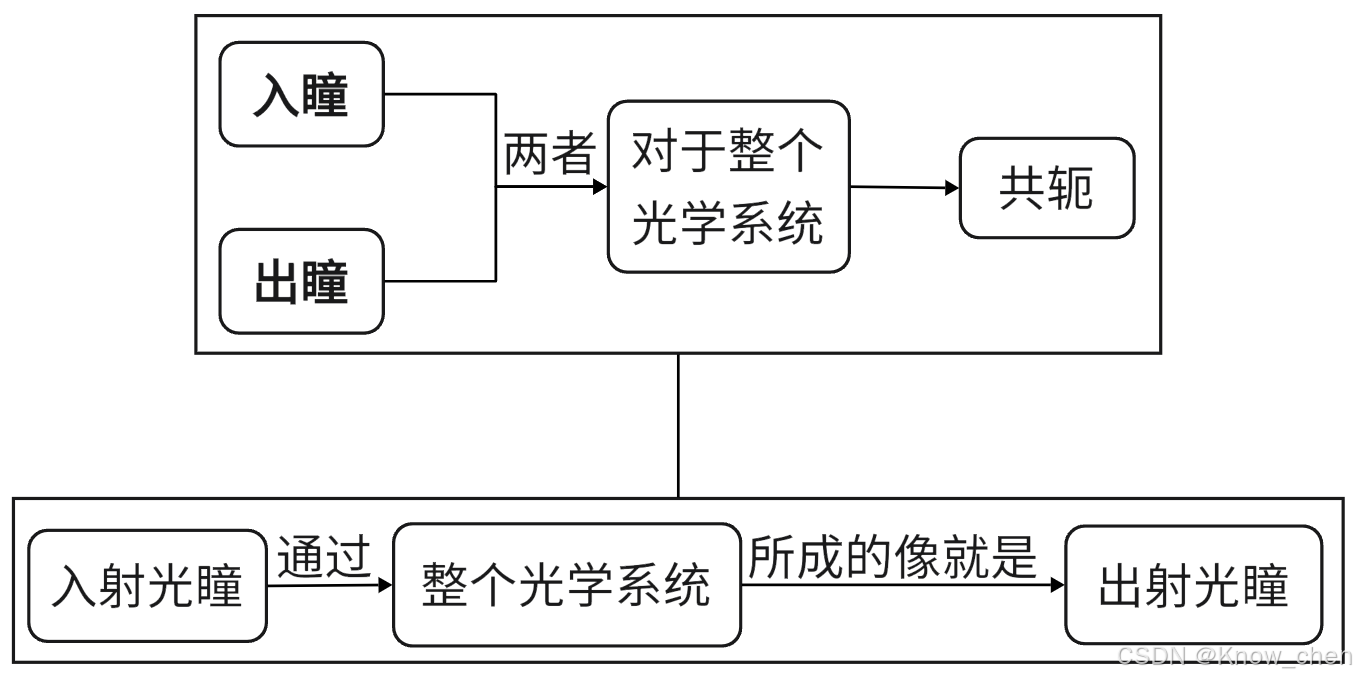
④孔径光阑
与入射光瞳、出射光瞳对应的那个实际起着限制作用的光孔Q1QQ2,即为孔径光阑。
如果光阑在整个系统的像空间,那么它本身也是出射光瞳。反之,在物空间,它就是入射光瞳。

⑤对物面中心的张角、边缘光光路计算的孔径角、第一辅助光线、对称式系统
对物面中心的张角:
将光学系统中所有光学零件的通光孔(镜框)分别通过其前面的光学零件成像到整个系统的物空间去,入射光瞳必然是其中对物面中心张角最小的一个。
如图:
为3.2入瞳出瞳的图的简化图


如图:
为3.2入瞳出瞳的图的简化图

同理,使所有的光学零件的通光孔通过其后面的光学零件成像到像空间去,则出射光瞳对像面中心的张角最小,此即像方孔径角U'。
第一辅助光线

结构对称于光阑的对称式系统

3.3孔径光阑、入射光瞳和出射光瞳之间的关系,主光线
①主光线

②第二近轴光线

③理想像高

④孔径光阑、入射光瞳和出射光瞳之间的关系

位置公式:


推导过程:
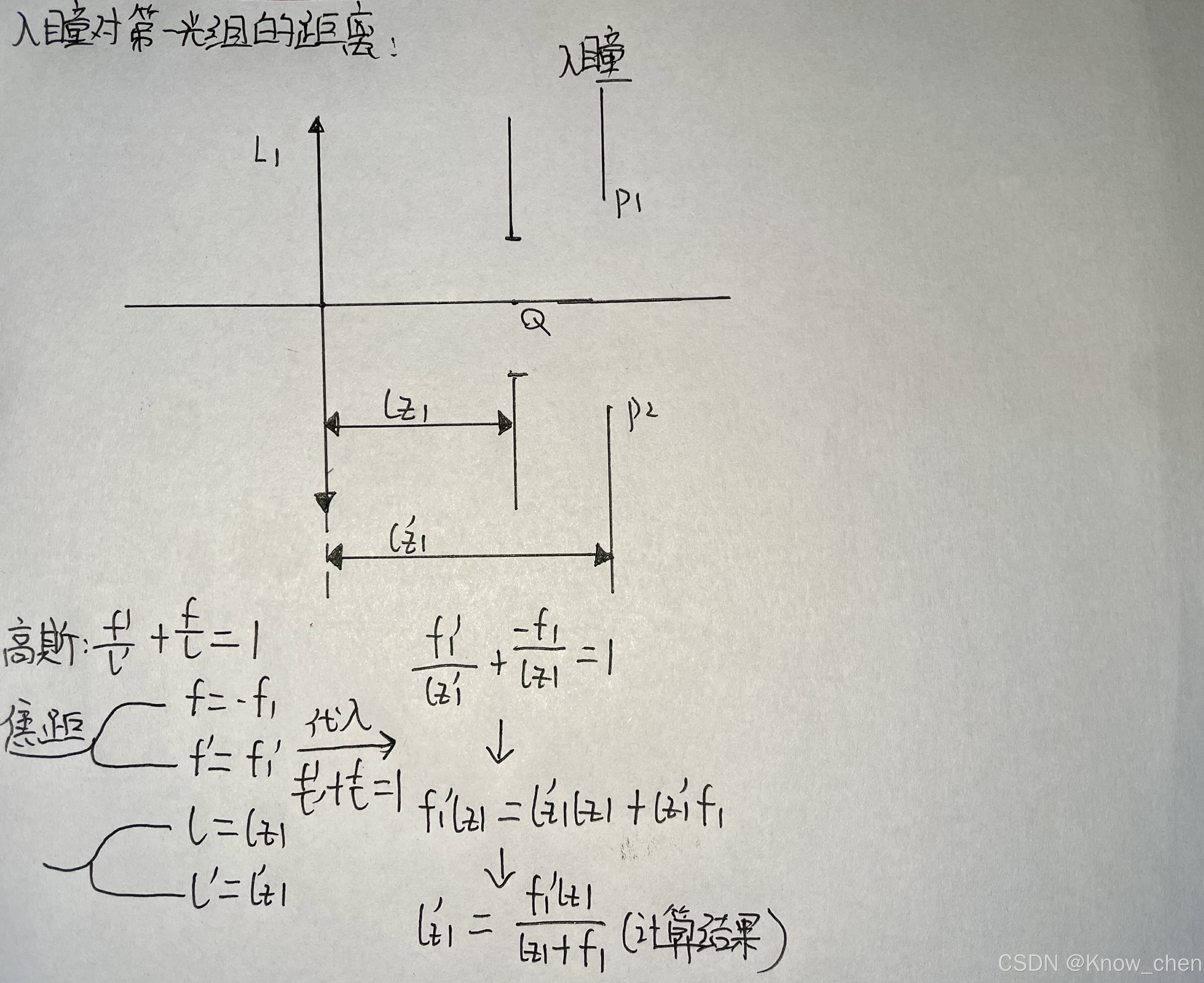
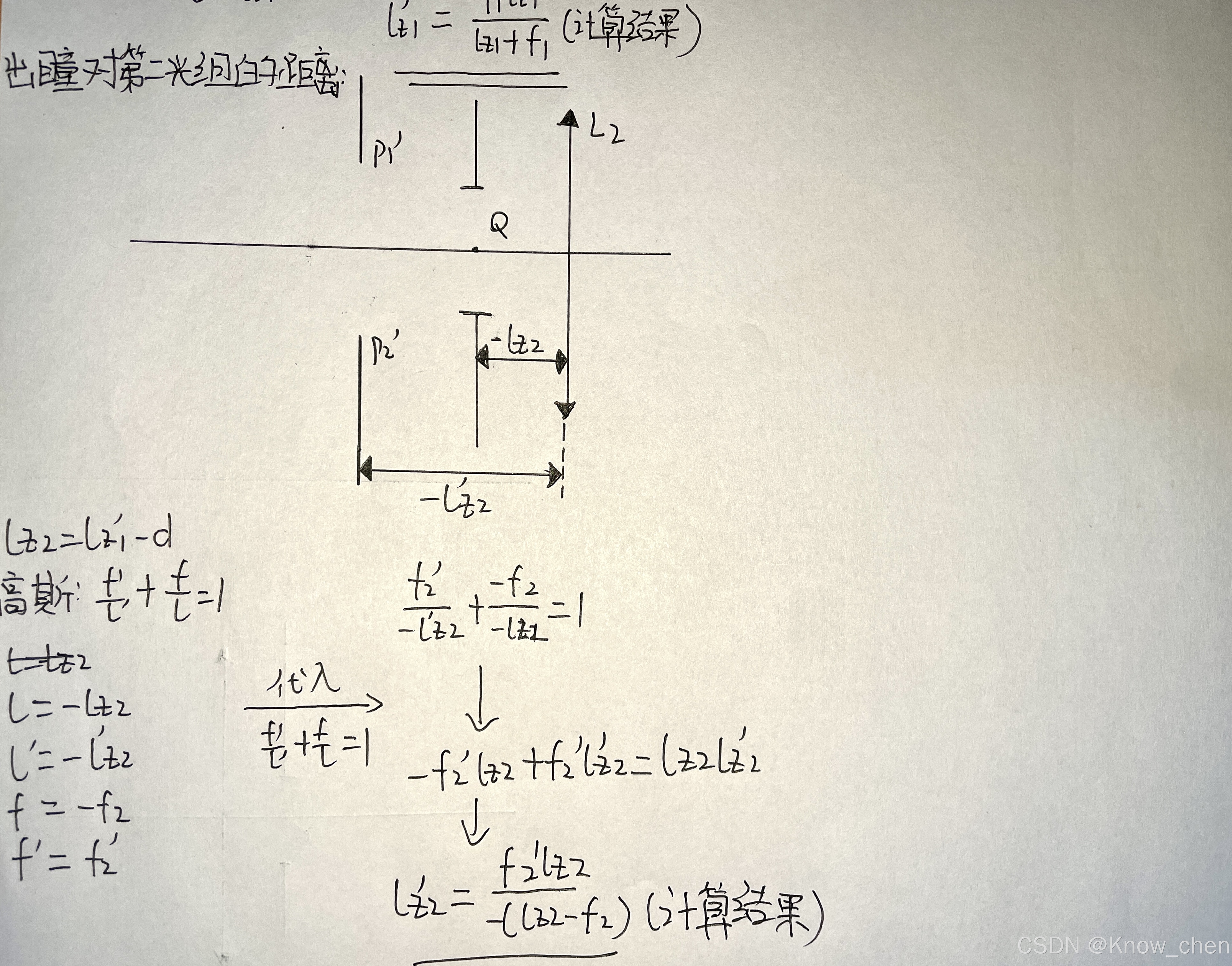
垂轴放大率β:

孔径角u

相对孔径、F数、数值孔径NA:
3.4以光瞳中心为坐标原点的物像关系
以光瞳中心为坐标原点的物像共轭点A和A'的位置分别以p和p'表示
Xz和Xz'分别是以光学系统的前、后焦点为坐标原点所表示的入射光瞳和出射光瞳的位置。

①垂轴放大率β

②以入射光瞳中心为坐标原点的物像位置关系公式

③对称式物镜

④光瞳处的拉赫不变量

式中,hz和hz'分别为第一近轴光线与入射光瞳和出射光瞳平面相交的高度,uz1和uzk' 分别为第二近轴光线在物像空间和光轴的夹角。
3.5视场光阑
3.5.1视场光阑的概述

3.5.2视场光阑的使用条件


3.5.3视场

如何求光瞳角放大率?

视场角和线视场的关系

物体在无限远处的计算

如果视场光阑为长方形或正方形,则其线视场按对角线计算。
3.6渐晕光阑
3.6.1渐晕光阑的概述


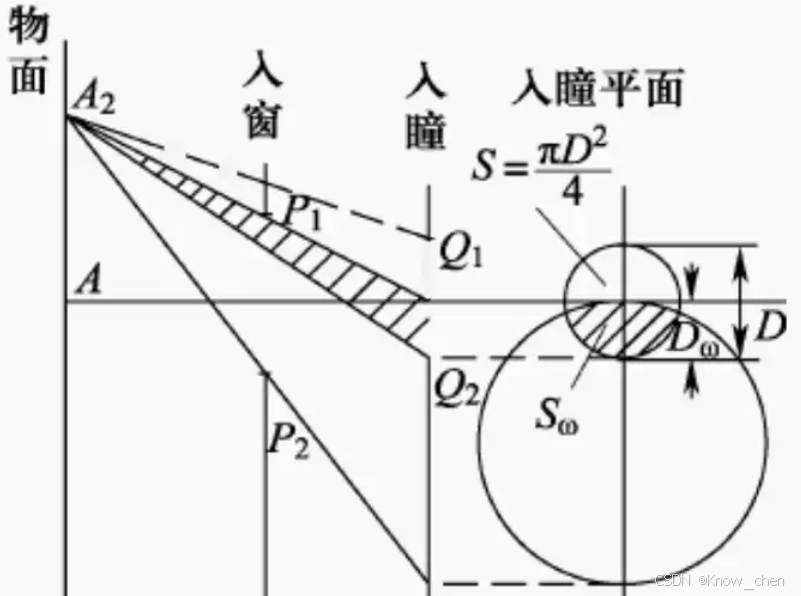
3.6.2入射/出射窗、渐晕的形成和作用效果
入射窗和出射窗:

渐晕的形成:
为说明渐晕的形成,略去光学系统的其他光孔,仅画出物平面、入射光瞳平面和入射窗平面来分析物空间轴外光束的渐晕。可分成三个区域来讨论:
①AB1为半径的圆形区域
每一个点均以充满入射光瞳的全部光束成像。
在入射光瞳平面上的成像光束如(a)

②以 B1B2绕光轴旋转一周所形成的环形区域
在此区域内,已不能使所有点以充满入射光瞳的光束通过光学系统成像。在子午面内,由点B1到点B2通过入射光瞳的光束由100%到50%渐变,这就是轴外点的渐晕。
B2点在入瞳面的成像如图(b):

③以 B2B3绕光轴旋转一周所形成的环形区域
在此区域内各点的光束渐晕更为严重,由点B2到点B3,通过入射光瞳的成像光束由50%到0。
B3点在入瞳面的成像情况如图(c):



3.6.3对称式光学系统的光束限制


3.6.4成像物体成无限远时的渐晕


渐晕的作用可使光学系统的横向尺寸减小,也可以把像质差的一部分光束拦掉,适当改善成像质量。但由于渐晕,轴外点成像的光照度是要降低的
3.6.5消除渐晕的条件



3.6.6渐晕系数

(补充一个Dw的图,如下)
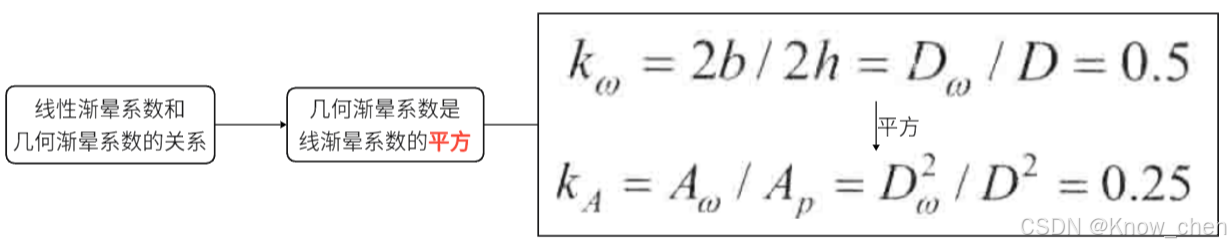
3.7消杂光光阑
3.7.1消杂光光阑概述
杂散光的产生:

杂散光的危害:

杂散光的分类:

3.7.2消杂光光阑的应用(遮光罩)
消杂光光阑一种通常的用法是装在仪器物镜的前面,即遮光罩
若物镜前面没有任何光阑时,物空间内约2π角度内的光线均可射入物镜,则镜筒内壁等非工作表面将被照射大量光能,形成杂散光。为此,加上遮光罩可以拦掉视场以外的光线射入物镜的入射光瞳。
遮光罩设计的要求:
遮光罩的设计应使任何直射到其内表面的光线经第一次反射后不能射入物镜的入射光瞳。
遮光罩的计算公式:


遮光罩内消杂光光阑的数目和位置的确定(作图法):
给定遮光罩长度L或直径D1以后,在遮光罩内消杂光光阑的数目和位置可用作图的方法确定。
作图法:
①第一个第二个光阑位置的确定
如图:


②第n个光阑位置的确定


③最后一个光阑位置的确定


四、光学系统的景深
4.1空间像

4.2空间像的成像


①空间点得到平面像的办法

②弥散斑

弥散斑大小与入射光瞳的直径有关,入射光瞳的直径减小,这些弥散斑也随之减小。

③透射失真



④景像畸变


4.3光学系统的景深
4.3.1景像平面成清晰像的条件

4.3.2景深、远景、近景及相关计算公式

入瞳直径=2a
出瞳直径=2a'
①景深计算公式

②弥散斑直径公式


可见,景像平面上弥散斑的大小除了与入射光瞳的直径有关,还与距离p1、p2和p有关。
③光学系统的正确成像(弥散斑直径允许值及正确透视)




即相当从入射光瞳中心来观察对准平面时,其上的弥散斑直径z和z'对眼睛的张角也不应超过眼睛的根限分辨角。
④弥散斑直径允许值确定后的景深公式

⑤对无限远处成清晰的像

五、远心光路
光学仪器中有相当大的一部分仪器用来测量长度。

①物方远心光路
(a)上述第一种测量类型的测量原理

(b)第一种测量类型的测量精度(视差)



(c)测量误差的修正



(d)物方远心光路的定义
因为这种光学系统物方主光线平行于光轴,主光线的会聚中心位于物方无限远,故称之为物方远心光路。

②像方远心光路
(a)上述第二种测量类型的测量原理


(b)第二种测量类型的测量精度(视差)
和第一种情况一样,都是因为视差,标尺的像不与分划板刻线平面重合。
(c)测量误差的修正

(d)像方远心光路的定义
因为这种光学系统的像方主光线平行于光轴,其会聚中心在像方无限远处,故称之为像方远心光路。


























 4563
4563

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








