一文讲清楚理想光学系统[2/2]。[光学学习笔记Light4]易懂，新手向。

关键词：

光组的组合、截距计算法、正切计算法、透镜焦距公式、薄透镜、实际光学系统的近轴区、望远镜系统、显微镜系统、照相机系统、实际光学系统的计算及系统的性质、等效系统、分划板、透镜性质、不同系统的光焦度公式。

一、文章总览：

二、光学系统的组合

2.1何为光组？

光组可以是单个透镜，也可以是复杂的透镜组。

光组可以单独看做一个理想光学系统

2.2何为等效系统？

一种通过简化或替代原始复杂光学系统来实现相同或近似光学效果的方法。

在光组的组合中：

等效系统是指由多个光组（可以是单个透镜或复杂的透镜组）组合而成的光学系统，其整体性能和行为可以通过一定的计算方法或公式来等效于一个单独的光学元件。

通俗来说：当多个光组组合在一起时，它们的共同作用可以视为一个等效的光学系统，该系统的焦距、主点位置等参数可以通过一定的方法计算得出。

2.3两光组的组合

2.3.1等效系统的像方参数：

物空间引一条平行于光轴的光线AQ，然后看图：

2.3.2等效系统的物方参数：

像空间引一条平行于光轴的光线S'Q2'，然后看图：

2.3.3等效系统的焦点和主点位置的确定：

如图可得物方参数(像方同理:

2.3.4以光组焦点为坐标原点的等效系统基点位置和焦距的计算：

①X'f/Xf

像方

物方：

②焦距位置

物方：

像方：

③主点位置

④垂轴放大率

2.3.5以光组主点为坐标原点的等效系统基点位置和焦距的计算：

①焦距位置

②主平面位置

2.4多个光组组合

两个光组的计算办法用于多个光组组合的计算太过复杂，因此多个光组的和组合，用以下计算方法。下列方法主要用于计算f/f'。

2.4.1正切算法

依赖hk和Uk'来计算，通过求出hk和Uk'这两个量来计算其他参数。

对于三个光组，由图可得：

同理，由k个光组组成的光学系统：

只要知道hk和U'k就能求出焦点位置

特殊例子计算过程：

2.4.2截距计算法

通过l来求f',l需要依赖于高斯公式计算。

利用这一公式求光学系统的焦距时，需先用高斯公式依次求出该光学系统中每一个光组的物距和像距，代入上式即可。

2.4.3各光组光焦度对等效系统光焦度的贡献

系统的总光焦度和各光组光焦度间的关系式：

当h1=1时:

说明具有一定光焦度的光组随其所处位置不同对总光焦度的贡献也不同

三、透镜

3.1单个折射球面的焦距

单个折射球面示意图：

物方和像方主面重合（如果无法理解建议先看我文章light系类的Light3，了解主平面的定义）

当考虑近轴光线时，两个主面将和球面顶点相切。如上图。

f/f’焦距公式：

单个球面的焦距公式：

3.2透镜的焦距公式

透镜在空气中：

①焦距公式

②光焦度公式

因为透镜在空气中，f=-f，设有：

③lF'和lF公式

④lH’和lH公式

代入①焦距公式可得

3.3典型透镜性质表

3.3.1决定透镜性质的参数

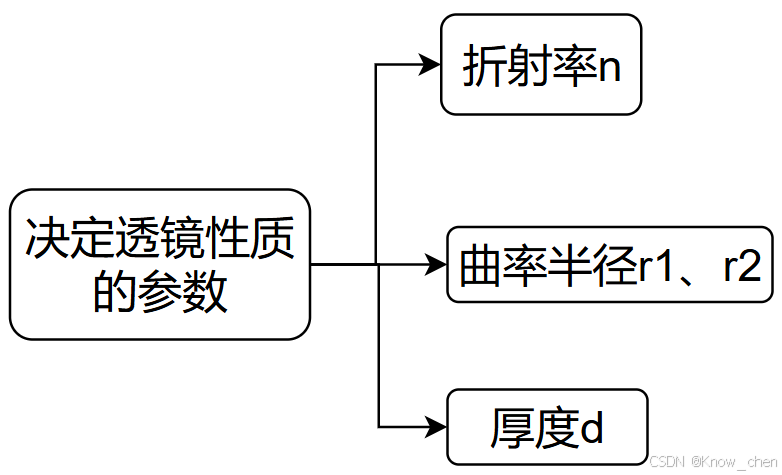
3.3.2透镜性质表

总结：

① 对于双凹、平凸、平凹和正弯月形透镜，其焦f"的正负，即会聚或发散的性质决定于其形状或曲率半径的配置。

②对于双凸透镜和负弯月形透镜，曲率半径固定后，厚度的变化可使其焦距为正值，负值和无限大
值。也可使主面在透镜以内，互相重合，透镜以外或无限远处。

③ 平凸和平凹透镜的主面之一与透镜球面顶点重合，另一主面在透镜以内距平面 d/n 处

④ 正弯月形透镜的主面位于相应折射面远离球面曲率中心一侧:负弯月形透镜的主面位于相应折射面靠近曲率中心的一侧。

这两种弯月形透镜的主面可能有一个主面位于空气中，或两个主面同时位于空气中，这由两个曲率半径和厚度的数值决定。

⑤实际上透镜厚度都是比较小的，很少用特别厚的透镜。上面表中对于透镜厚度变化的分析只是为了有助于对透镜光学性质的了解。

3.4薄透镜

3.4.1薄透镜的定义

3.4.2薄透镜的性质

3.4.3薄透镜的组合

由双薄透镜组合的公式可知：

当间隔d由小变大时，双薄透镜组合光组的光焦度：可能由正(会聚系统)变为零(望远系统)或变为负(发散系统)。

四、实际光学系统焦点位置和焦距的计算

4.1实际光学系统的近轴区具有理想光学系统的性质

可以认为共轴球面系统的近轴区就是实际的理想光学系统，理想光学系统理论可以适用于实际光学系统的近轴区。所以，

实际光学系统的基点位置和焦距是指近轴区的基点位置和焦距。

4.2实际光学系统的基点和焦距的计算

因为实际光学系统的基点位置和焦距是指近轴区的基点位置和焦距。所以简便的方法是用近轴光光路计算公式对实际系统作光路计算。

近轴光路计算公式：

将这些公式列成表格，以便于用计算器进行计算，如下表（正向光路计算示例）

求物方基点时，把光学系统反转，利用一样的办法计算，这个过程就被称为反向光路计算。

五、几种典型系统的理想光学系统性质

5.1望远系统

5.1.1有限焦距系统，无焦系统

5.1.2望远系统（无焦系统）

①焦距

②放大率

1.垂轴放大率/物像公式

2.轴向放大率

3.角放大率

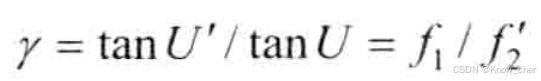
4.望远系统在空气中

5.三种放大率之间的关系

由上可见，一般光学系统的各放大率之间的关系也适用于望远系统。

③望远镜的两种最基本形式

分划板：

定义：分划板是一块极薄的表面刻有分划密位线的薄玻璃，它位于望远镜的光学系统焦面上，作为平面光学元件存在。

分划板上刻有各种特定的标记，如视距刻度线、十字丝、小圆点和小圆圈等，用于对外界物体的瞄准和测量。

作用：定位和测量、提高测量精度、辅助观测

两种最基本形式：

伽利略望远镜系统：

开普勒望远镜系统:

5.1.3望远系统的组合

例子，如下图：

合成后等效系统的焦距为：

或

f2'为所加的有限焦距系统的焦距;   β1、γ1为前面望远系统的垂轴放大率和角放大率。

总结：

上式表明，在一个有限焦距的光学系统之前加一个角放大率为γ的望远系统时，

整个系统的焦距为原有限焦距系统的焦距的γ倍。

5.2显微镜系统

①焦距公式（组合焦距）

②放大率

1.目镜放大率:

2.物镜放大率:

3.组合放大率:

轴向放大率：

角放大率：

③成像

显微镜成像示意图：

5.3照相物镜系统

①放大率

一般对无限远处物体成像所以：

②调焦

照相物镜成像示意图：

③成像曲线

照相时必须成实像在胶片上，所以永远成倒像

x/f和垂轴放大率的关系曲线示意图：