工程经济期末（一）

最新推荐文章于 2025-04-23 08:15:00 发布

Epiphanywh

最新推荐文章于 2025-04-23 08:15:00 发布

阅读量1.3k

点赞数 12

文章标签：其他经验分享

本文链接：https://blog.csdn.net/2201_75479723/article/details/144181172

版权

工程经济引入

什么是工程经济学？

工程经济学是研究工程技术学与经济的学科。

详细介绍

工程经济学是一门融合了工程学与经济学基本原理和方法的交叉学科，旨在对工程项目进行经济分析与评价，为工程技术方案的优选、项目的投资决策以及项目实施过程中的成本控制等提供科学依据。

核心内容

成本效益分析：它着重考量工程项目在整个生命周期内的投入成本（包含初始投资、运营成本、维护成本等）以及所能产生的效益（如经济收益、社会效益等），通过一定的方法将不同时间点上的成本和效益换算到同一时间基准上进行对比分析，从而判断项目是否值得实施。例如，建设一座新的工厂，要分析建设厂房、购置设备等初始投资，还有后续每年的原材料采购、员工工资等运营成本，同时预估产品销售带来的收益，权衡总体的成本效益情况。
资金的时间价值：资金在不同时间点上具有不同的价值。同样一笔钱，现在拥有和一年后拥有，其价值是不一样的，因为现在的钱可以通过投资等方式获取额外的收益。所以在分析工程项目时，需要运用诸如复利计算、净现值、内部收益率等方法，把不同时间发生的资金流量折算到同一时间去衡量。比如把未来若干年的收益按一定利率折算到项目开始投资的时间点，来和初始投资比较。
方案比选：针对一个工程项目往往会有多个可行的技术方案或者建设方案，工程经济学通过经济评价指标（如投资回收期、净现值、内部收益率等）来对比各个方案的优劣，帮助决策者挑选出最经济合理的方案。例如在一条道路建设中，有不同的施工工艺、材料选择等构成的多个方案，通过分析各方案的成本、收益以及资金时间价值等因素，确定最佳方案。

为什么要学习工程经济学？

以有限的资金，得到最大的经济效益。

避免盲目投资
优化方案选择

如何利用工程经济学？

在这里插入图片描述

考点

在这里插入图片描述
题型：

单选题
判断题
计算题

其中计算题的范围：

第二章一个大题
第五章两个大题：一是评价指标；二是盈亏平衡分析
第九章两个大题：挣值法；因素分析法
第十章两个大题：画网络图；六时标注法

现金流量与资金时间价值

1. 现金流量

现金流量是指工程项目在生命周期内所发生的资金流入或流出。

现金流出： 相对某个系统，指在某一时点上流出系统的资金或货币量，如投资、成本费用等。(CO-case out)
现金流入： 相对一个系统，指在某一时点上流入系统的资金或货币量，如销售收入等。(CI-case in)
净现金流量： 同一时点上，现金流入与现金流出的代数和。即 净现金流量=现金流入-现金流出。

2. 现金流量图

现金流量图是一种直观展示工程项目在整个生命周期内现金流入、流出情况以及其发生时间节点的图示工具。它以时间为横轴，以现金流量为纵轴，将复杂的资金收支情况通过图形清晰地呈现出来，便于分析人员快速把握项目资金流动的全貌。

在这里插入图片描述

构成要素

横轴（时间轴）：代表项目从开始到结束所经历的各个时间阶段，时间单位可以是年、月、季度等，根据项目具体情况和分析精度要求来确定。比如一个为期 5 年的工程项目，横轴就会依次标注从第 0 年（代表项目开始的初始时刻）到第 5 年的各个时间节点。
纵轴（现金流量轴）：体现现金流入或流出的数值大小，单位一般是货币单位，如人民币元、美元等。现金流入用向上的箭头表示，意味着资金进入项目，例如项目产品的销售收入、投资收益等；现金流出用向下的箭头表示，代表资金从项目中支出，像初始投资、每年的运营成本、设备维护费用等。现金流量的大小（现金流量数额），用箭头的长短会意表示。
作用点（现金流量发生的时点，通常表示该时间点末的时间）。

横轴表示时间也表示技术方案本身，0为起点，表示现在，向右延伸表示时间的延续。

在这里插入图片描述

绘制现金流量图

参考哔哩哔哩视频：BV1db4y1d7yz
在这里插入图片描述
这里主要注意，年末、年初等字眼。坐标点代表的是年末，如下标为5的点代表第五年年末、第六年年初。

在这里插入图片描述

现金流量表

现金流量表是将工程项目在一定时期内（通常涵盖项目全生命周期）的所有现金流入和现金流出按照特定的分类和时间顺序进行详细罗列的表格形式的记录文件。它系统地反映了项目各个阶段资金的来源与去向，是进行项目财务分析和经济评价的重要依据。

基本结构和内容：
一般分为表头、表体两大部分。表头包含项目名称、编制单位、报表期间（如某年某月至某年某月或者项目第几年到第几年等）等基本信息。
表体主要包含以下几列内容：
- 序号：对各现金流量项目进行顺序编号，方便查阅和引用。
- 项目：详细列出不同类型的现金流入和现金流出项目名称，例如现金流入方面有销售收入、补贴收入、回收固定资产余值等；现金流出方面有建设投资、流动资金、经营成本、税金及附加等。
- 计算期（时间阶段）：明确对应现金流量发生的具体时间阶段，与现金流量图的时间轴相对应，通常按年依次罗列项目各年情况，也可以根据需要细化到季度、月等更短的时间周期。
- 现金流入量：具体填写对应项目在相应时间阶段内实际发生的现金流入数值，各流入项目数值相加得出该阶段总的现金流入量。
- 现金流出量：记录对应项目在相应时间阶段内的现金流出数值，同样各流出项目汇总得到总的现金流出量。
- 净现金流量：通过该阶段的现金流入量减去现金流出量计算得出，它直观反映了项目在该时间点上资金的净收支情况，是分析项目盈利能力等的关键指标。

在这里插入图片描述

3. 资金时间价值

在这里插入图片描述

4. 资金时间的计算

利息与利率

在这里插入图片描述
公式：

在这里插入图片描述

单利计算

单利(Simple Interest)：利不生利，即计算利息仅考虑最初的本金，不考虑本金所产生的利息。其计算式如下：
在这里插入图片描述

当有n个计息期时，所付或所收的单利总和为n期之和：

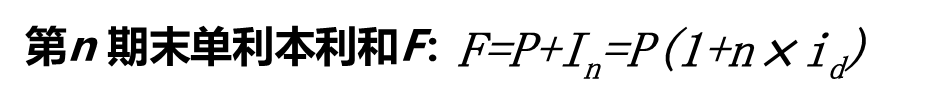
在这里插入图片描述

5. 复利公式

复利(Compound Interest)：利生利，利息是上一期期末的本利和产生的。表达式如下：
在这里插入图片描述

计算公式：

其中的年金是指，大小相等、时间间隔相等的金额（时间间隔不一定是一年）。

注意： 在等额支付中，年金是年末值。使用年金求的现值是第一个A出现时间点前一个时间点的现值；使用年金求的终值是最后一个A出现时间点的终值。

6. 等值计算

由于资金具有时间价值，即使金额相等，因其发生在不同时点，其价值就不相同。反之，不同时点绝对值不等的资金在时间价值的作用下却可能具有相等价值。这些不同时期、不同数量但其价值等效的资金称为“等值”。

两笔资金金额相同，在不同时间点：在资金时间价值的作用下，两笔资金不可能存在等值关系。
两笔金额不等的资金，在不同时间点：在资金时间价值的作用下，两笔资金有可能等值。
两笔金额不等的资金，在不同时间点：在资金时间价值的作用下，如果在某个时间点等值，则在利率不变的情况下在其他时间点上它们也等值。
两笔资金金额相同，在同一时间点上：在资金时间价值的作用下，两笔资金等值。
两笔资金金额不同，在同一时间点上：在资金时间价值的作用下，两笔资金不等值。

影响资金等值的因素有3个：

资金数额的多少
资金发生时间的长短
利率的大小

在工程经济分析中，考虑资金时间价值的情况下，不同时间发生的收入或支出因不具有时间的可比性是不能直接相加减的。利用等值的概念建立了时间可比条件，可以把不同时点发生的资金换算成同一时点的等值资金，然后再进行比较。所以，在工程经济分析中，方案比较都采用等值概念来进行分析、评价和选定。

例题

某企业在城郊租用了一处仓库，合同期限10年，有两种租金支付方式：一是每年年初支付，年租金10万元；二是一次性支付租金80万元，基准收益率8%。试分析哪种方式对企业更合算？

主要思路是将两种资金换算成同一时间点上的资金，进行比较大小。

注意： 第一种支付方式中，是年初支付年租金，该值不是年金。真正的年金是在年末支付，所以在使用年金求得现值时，需要先将年初支付年租金转换为年末支付的年租金。

在这里插入图片描述

在这里插入图片描述

这里使用年金求得终值，得到的是第5年年末的本利和，而不是第7年的本利和。

因此，还需要将第5年年末的本利和看作是现值，求得两年后（第7年）的终值。

7. 名义利率与实际利率

当利率的时间单位与计息周期不一致时，若采用复利计息，会产生名义利率与实际利率不一致问题。

在这里插入图片描述

名义利率r：计息周期利率乘以每年计息周期数得到的年利率。
在这里插入图片描述
通常指一年内多次计息时给出的年利率；以一年为计息基础，等于每一计息期的利率与每年的计息次数的乘积。

实际利率考虑了资金时间价值的实际年利率。
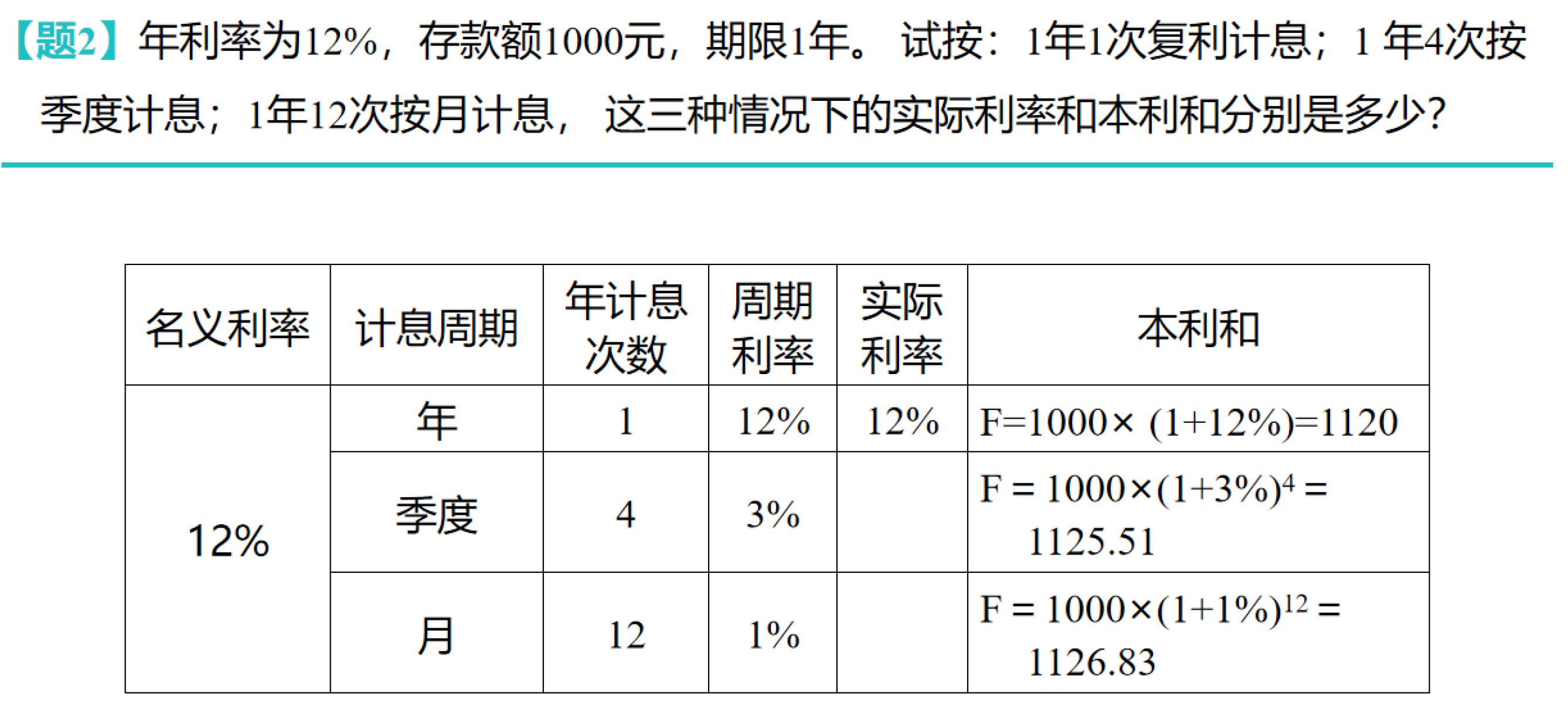
在这里插入图片描述

例题：

在这里插入图片描述

本题考查资金等值计算，我们需要先根据给定的计息周期和年利率求出实际利率，再利用等额支付现值公式来计算与其等值的第0年的现值，以下是具体步骤：

步骤一：计算实际利率

已知年利率 $10\%$ ，每半年计息一次，一年计息次数 $n = 2$ 。这里的年利率 $i$ 是名义利率，需要将其转换为周期利率，再使用周期利率计算出有效利率/实际利率。

根据实际利率计算公式 $i_{eff}=(1 + \frac{r}{n})^n - 1$ （其中 $r$ 为名义利率， $n$ 为一年内的计息次数），可得：

$\begin{aligned} i_{\text{eff}} &= \left(1 + \frac{10\%}{2}\right)^2 - 1 \\ &= (1 + 0.05)^2 - 1 \\ &= 1.05^2 - 1 \\ &= 1.1025 - 1 \\ &= 0.1025 \\ &= 10.25\% \end{aligned}$

步骤二：利用等额支付现值公式计算现值

已知连续 $3$ 年的等额年末支付 $A = 500$ 万元，期数 $n = 3$ ，实际利率 $i_{eff}=10.25\%$ 。

等额支付现值公式为 $A\times\frac{(1 + i)^{n}- 1}{i\times(1 + i)^{n}}$ （这里的(i)为实际利率），将相应数值代入可得：

$\begin{aligned} P &= 500 \times \frac{(1 + 0.1025)^{3} - 1}{0.1025 \times (1 + 0.1025)^{3}} \\ &= 500 \times \frac{1.1025^{3} - 1}{0.1025 \times 1.1025^{3}} \\ &\approx 500 \times \frac{1.3382 - 1}{0.1025 \times 1.3382} \\ &\approx 500 \times \frac{0.3382}{0.1372} \\ &\approx 1228.13 \text{（万元）} \end{aligned}$

所以，与其等值的第 $0$ 年的现值约是 $1228.13$ 万元。

在这里插入图片描述

首先，计算实际利率：
- 已知年利率 $8\%$ ，每季度计息一次，一年计息次数 $n = 4$ 。
- 根据实际利率公式 $i_{eff}=(1 + \frac{r}{n})^{n}-1$ ，其中 $8\%$ ， $n = 4$ 。
- 代入可得 $i_{eff}=(1+\frac{0.08}{4})^{4}-1=(1 + 0.02)^{4}-1$ 。
- 计算 $1 + 0.02)^{4}=1.02^{4}=1.08243216$ 。
- 所以 $i_{eff}=1.08243216-1 = 8.243216\%\approx8.24\%$ 。
然后，计算季度数(m)：
- 借款时间为 $16$ 年，每季度借款一次，所以季度数 $m=16\times4 = 64$ 。
接着，计算等额支付系列终值：
- 每季度末借款(A = 1400)元。
- 根据等额支付系列终值公式 $A\times\frac{(1 + i)^{m}-1}{i}$ ，这里 $i_{eff}\div4$ （因为公式中的(i)是计息周期利率）， $i_{eff}=8.24\%$ ，则 $i=\frac{0.0824}{4}=0.0206$ 。
- 代入公式可得 $1400\times\frac{(1 + 0.0206)^{64}-1}{0.0206}$ 。

所以，与其等值的第 $16$ 年末的将来值为 $182815.5$ 元。

注意：

不能把每季度借款 $1400$ 元转换为一年借款 $5600$ 元时。这里存在一个问题。因为每季度借款 $1400$ 元是一个等额支付系列，并且是按季度计息的。如果简单地将其转换为一年借款 $5600$ 元，会破坏等额支付系列按季度发生的特性，导致计算错误。
按照等额支付系列终值的原理，必须按照实际的支付周期和计息周期来计算。

工程项目经济评价办法

在这里插入图片描述
重点： 净现值、内部收益率、投资收益率、静态投资回收期

净现值

净现值是用一个预定的基准收益率(或设定的折现率)，分别把技术方案整个计算期间内各年所发生的净现金流量都折现到技术方案开始实施时的现值之和。

在这里插入图片描述

在这里插入图片描述

净现值与基准收益率之间的关系：

净现值和折现率之间的关系：

净现值和投资回收期之间的关系：

例题

在这里插入图片描述

某企业需要一台汽车，有买车和租车两个方案：购车费53000元，4年后转让价值11000元，使用费用第一年7500元，以后每年增加500元；租车方案，年租车费15000元（年初支付），使用费用比购车方案每年少1000元，当i=10%时，请选择最优方案。

在这里插入图片描述

净现值率

净现值率为NPVR（Net Present Value Rate），下图中给出的英文有问题~

在这里插入图片描述
作用： 净现值率常常用于多方案投资的优劣排序：净现值率越高，单位投资所获取收益的能力越大，该方案越好。

在这里插入图片描述

该题目主要用的知识点是，净现值是未来总报酬的总现值与初始投资现值之差。

基准收益率

在这里插入图片描述

内部收益率

在这里插入图片描述
这个公式求得的是折现率。

在这里插入图片描述
这里的相似三角形具体是指：

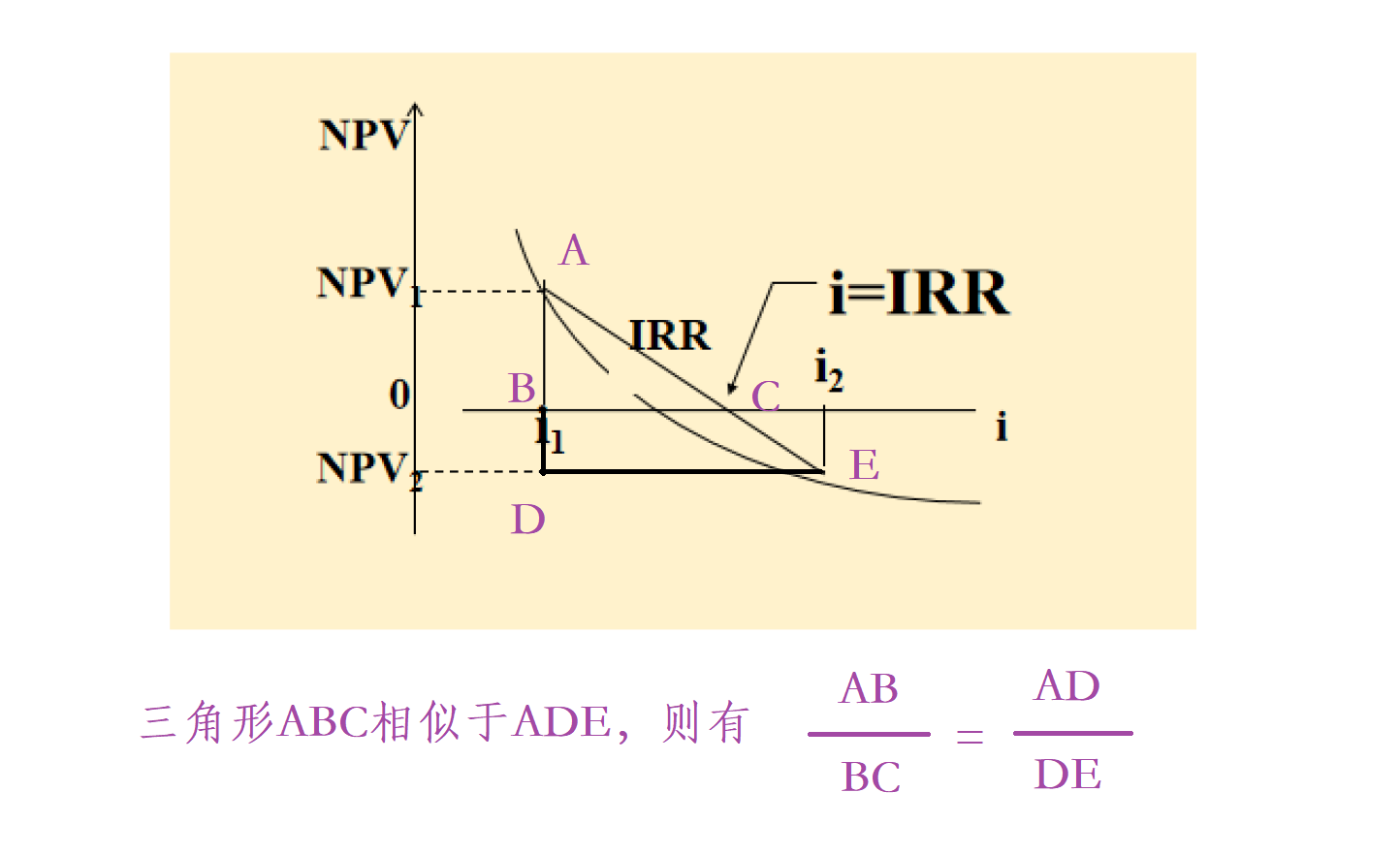
其中 $AB = NPV_1$ ， $BC = IRR - i_1$ ； $AD = NPV_1 + NPV_2$ ， $DE = i_2 - i_1$

最后整理后，就可以得到求IRR的公式了。

在这里插入图片描述

例题

在这里插入图片描述

净年值

在这里插入图片描述

先计算净现值
将净现值看作本金P，求得A

在这里插入图片描述

投资回收期

静态回收期

在这里插入图片描述
这里第一种情况，“项目建成后各年净收益均相同”如：

也就是说，需要10个单位时间才能将投资1000全部回收。（但是这种场景在做题时比较少见~）

这里的0年的初始投资/总投资 = 建设投资 + 流动资金，并且是融资前的分析（不包括贷款）。

以下是常见第二种情况的计算：
在这里插入图片描述

动态回收期

在这里插入图片描述

投资收益率

投资收益率是衡量技术方案获利水平的评价指标，它是技术方案建成投产达到设计生产能力后一个正常生产年份的年净收益额与技术方案投资的比率。

在这里插入图片描述
注意这里的投资收益率和总投资收益率之间的关系。

在这里插入图片描述

年息税前利润 = 年利润总额 + 计入年总成本费用的利息费
总投资 = 建设投资 + 建设期贷款利息 + 流动资金

例题：
在这里插入图片描述

在这里插入图片描述

年净利润 = 利润总额 - 所得税
资本金 = 总投资 - 债务资金

例题：
在这里插入图片描述

互斥方案

在这里插入图片描述

静效益值法

在这里插入图片描述

例题
在这里插入图片描述

内部收益率法

在这里插入图片描述

例题
在这里插入图片描述

最小公倍数法

在这里插入图片描述
例题：

盈亏平衡分析

盈亏平衡分析(Break-Even Analysis)是指项且达到设计生产能力的条件下，通过计算盈亏平衡点(BEP，Break-Even Poit)，分析项目成本与收益的平衡关系，判断项且对产出品数量变化的适应能力和抗风险能力。盈亏平衡分析只用于财务分析。

参考BiliBili视频：BV1ks4y1z7T1
在这里插入图片描述

在这里插入图片描述