模型解释工具：SHAP --- 论文实战

一、前言

        模型可解释性指对模型内部机制的理解以及对模型结果的理解，即模型中的那些特征最重要；哪个特征造成效果的好与不好。

        在众多模型中，可解释性最强的当然是线性模型；但是由于线性模型在特征提取方面存在天然的弱势，以及过于依赖原始的特征工程，在稍微复杂一些的场景中，基本见不到线性模型的影子。现在效果比较好的几类模型，SVR、 neural network 模型可获得较好的效果，但他们同时也被称为“黑盒”模型，原因是这类模型不能描述特征重要性。所以，打开“黑盒”模型就成了一个值得研究的课题。

       关于模型解释性，除了线性模型和决策树这种天生就有很好解释性的模型以外，sklean中有很多模型都有importance这一接口，可以查看特征的重要性。其实这已经含沙射影地体现了模型解释性的理念。只不过传统的 importance 的计算方法其实有很多争议，且并不总是一致。

二、 模型可解释性工具 SHAP

       Shapley value 最早由加州大学洛杉矶分校（UCLA）的教授 Lloyd Shapley 提出, 主要是用来解决合作博弈论中的分配均衡问题。Lloyd Shapley 是 2012 年的诺贝尔经济学奖获得者，也是博弈论领域的无冕之王。

   

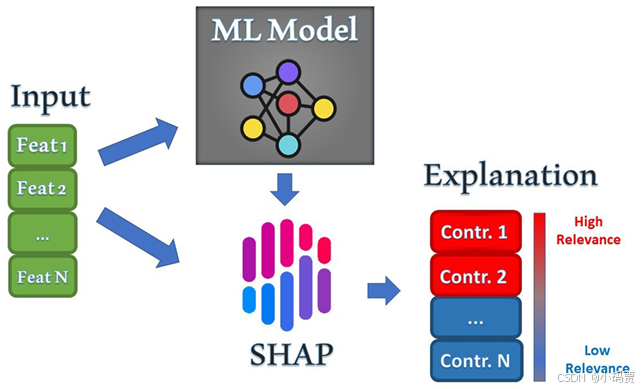
        SHAP，作为一种经典的事后解释框架，可以对每一个样本中的每一个特征变量，计算出其重要性值，达到解释的效果。该值在 SHAP 中被专门称为 Shapley Value。因此 Shapley Value 是 SHAP 方法的核心所在，理解好该值背后的含义将大大有助于我们理解 SHAP 的思想。

        我们已有的数据集中会包含很多特征变量，从博弈论的角度，可以把每一个特征变量当成一个玩家。用该数据集去训练模型得到的预测结果， 可以看成众多玩家合作完成一个项目的收益。Shapley value，通过考虑各个玩家做出的贡献，来公平地分配合作的收益。

三、支持SHAP的模型

SHAP 可以用来解释很多模型。目前支持的模型有：

• Tree Explainer（树模型）：

  Tree Explainer 首先根据树结构将待解释样本划分为一个叶子节点，并计算该叶子节点对预测结果的贡献值。

  然后，从叶子节点开始向上遍历树结构，计算每个节点对预测结果的贡献差异，并根据特征的排序顺序依次累加每个特征的贡献，得到其 Shapley value。

• Kernel Explainer（核函数）：

  Kernel Explainer 首先通过随机抽样获取一组样本，并在这些样本上拟合一个全局模型。

  然后，在每个样本上，根据每个特征的取值和全局模型的预测值，构建一个新的局部模型。

  最后，通过核函数对每个局部模型进行加权平均，得到基于全局模型的 Shapley value 近似值。

• Deep Explainer（神经网络模型）：

  DeepExplainer 会首先通过正向传播计算出模型在待解释样本上的预测值和激活值。

  然后，通过反向传播计算各层梯度，将梯度乘以激活值，并根据 Shapley value 对每个神经元进行权重分配，得到每个特征的重要性贡献。

• Gradient Explainer（梯度信息）：

  GradientExplainer 首先选择一个参考点作为基准，并在该点处计算模型输出的梯度。

  然后，在每个样本上，通过对输入特征进行微小扰动来计算新的输入数据点，并计算模型输出的梯度差异。根据梯度的加权平均值，可以得到每个特征的 Shapley value 近似值。

• Linear Explainer（线性模型）：

  LinearExplainer 首先通过拟合一个线性模型来计算每个特征对预测结果的贡献值。

  然后，根据特征的排序顺序依次累加每个特征的贡献，得到其 Shapley value。

四、SHAP解释 

 4.1  导入Python库

'''====================导入Python库===================='''
import pandas as pd               #python科学计算库
import numpy as np                #Python的一个开源数据分析处理库。
import matplotlib.pyplot as plt   #常用Python画图工具
from xgboost import XGBRegressor  # 导入 XGBRegressor 模型
from sklearn.model_selection import train_test_split # 数据划分模块
from sklearn.preprocessing import StandardScaler   # 标准化模块
from sklearn.metrics import mean_squared_error, r2_score   #误差函数MSE,误差函数R^2,
from sklearn.model_selection import GridSearchCV     #超参数网格搜索
import shap  # 导入SHAP模型解释工具

 4.2 导入数据并标准化 

'''========================导入数据========================'''
data = pd.read_excel('D:/复现/trainset_loop6.xlsx')  #读取xlsx格式数据
# date = pd.read_csv('D:/复现/trainset_loop6.csv')   #读取csv格式数据
print(data.isnull().sum())   #检查数据中是否存在缺失值
print(data.shape)   #检查维度
print(data.columns) #数据的标签
data = data.drop(["PN","AN"], axis = 1) #axis = 1表示对列进行处理，0表示对行
Y, X = data['Eads'] , data.drop(['Eads'] , axis = 1) #对Y、X分别赋值
columns = X.columns


'''=========================标准化========================'''
#利用StandardScaler函数对X进行标准化处理
scaler = StandardScaler()
X = scaler.fit_transform(X)
'''====================划分训练集与测试集==================='''
X_train,X_test,y_train,y_test = train_test_split(X , Y , test_size=0.2 , random_state=42)

 4.3  XGBoost模型训练

'''=======================模型训练========================'''
#模型训练
model = XGBRegressor()   # 模型实例化。
'''========================超参数========================='''
# booster: 默认值为 ‘gbtree’，基于树模型。 ‘gblinear’ 基于线性模型。
# silent: 默认为0；当这个参数值为1时，静默模式开启，不会输出任何信息。
# nthread：默认值为最大可能的线程数。
# eta: 权重递减参数，典型值为0.01-0.2。
# min_child_weight：决定最小叶子节点样本权重和。
# max_depth：这个值为树的最大深度。
# max_leaf_nodes：树上最大的节点或叶子的数量。
# gamma：Gamma指定了节点分裂所需的最小损失函数下降值。 这个参数的值越大，算法越保守。
# max_delta_step：每棵树权重改变的最大步长。如果这个参数的值为0，那就意味着没有约束。
# reg_alpha：权重的L1正则化项。 可以应用在很高维度的情况下，使得算法的速度更快。默认为1。
# reg_lambda：权重的L2正则化项。默认为1。
# colsample_bytree:  # 对特征随机采样的比例;如本文有25个特征,colsample_bytree=0.8,则为25*0.8=20。
# objective: 'reg:linear'线性回归,'reg:logistic'逻辑回归,'binary:logistic'二分类问题,'multi:softmax'多分类,用num_class指定类别数
# eval_metric: 评估指标,‘rmse’回归;‘mlogloss’多分类;‘error’二分类;‘auc’二分类任务。

# 定义超参数网格。
n_estimators = [50,100,150]
max_depth = [2,3,4]
reg_alpha = [0.1,0.5,1.0]
reg_lambda = [0.1,0.5,1.0]
# min_samples_leaf = [1,3,5,7,9,11]  #有点费时间就没加这个超参数,想加的可以加,（不加可能会有点过拟合）。
# learning_rate = [0.1,0.5,1]  # 每棵树对最终预测的贡献,大的 learning_rate 能加快收敛速度，默认为0.1。

# 网格搜索,cv = 5 表示进行5折交叉验证
grid_search = GridSearchCV(estimator = model,cv = 5, param_grid={'max_depth': max_depth,"n_estimators":n_estimators,"reg_alpha":reg_alpha,"reg_lambda":reg_lambda}, scoring='neg_mean_squared_error')
grid_search.fit(X_train, y_train)
# 最佳模型
best_model = grid_search.best_estimator_
# 最佳超参数
best_max_depth = grid_search.best_params_['max_depth']
# best_min_samples_leaf = grid_search.best_params_['min_samples_leaf']
best_n_estimators = grid_search.best_params_['n_estimators']
best_reg_alpha = grid_search.best_params_['reg_alpha']
best_reg_lambda = grid_search.best_params_['reg_lambda']
print(f'Best max_depth:{best_max_depth:.3f}',"\n",f'Best n_estimators:{best_n_estimators:.3f}',  # ,"\n",用于换行
      "\n",f'Best reg_alpha:{best_reg_alpha:.3f}',"\n",f'Best reg_lambda:{best_reg_lambda:.3f}')

 4.4  SHAP解释模型

'''=====================SHAP解释模型======================'''
explainer = shap.TreeExplainer(best_model)  # 传入训练好的模型。
shap_values = explainer.shap_values(X_test)  # 这里拿验证数据集进行呈现。输入X_train拿训练数据集进行呈现。

shap.summary_plot(shap_values = shap_values,  # 一个数组，其中包含了样本的 Shapley 值，大小为 [n_samples, n_features]
                  features = X_test , # 一个数组，其中包含了样本的特征矩阵。这需要与 shap_values 中的样本数量一致。
                  feature_names = columns, # 特征名称列表，长度应该和 features 的列数相同。
                  max_display = 25,    # 可选参数，用于指定要显示的最多特征数量。默认情况下，将显示所有特征。
                  plot_type = "dot",  # 可选参数，用于指定图形类型。可以设置为 ‘dot’ 或 ‘bar’。
                  )

#summary plot是针对全部样本预测的解释，有两种图，‘bar’一种是取每个特征的shap values的平均绝对值来获得标准条形图，这个其实就是全局重要度，
# ‘dot’另一种是通过散点简单绘制每个样本的每个特征的shap values，通过颜色可以看到特征值大小与预测影响之间的关系，同时展示其特征值分布。

# feature_importance = pd.DataFrame()  #创建一个 DataFrame 来存储 feature_importance。
# feature_importance['feature'] = columns  # 给 'feature' 赋予特征名称。
# feature_importance['importance'] = np.abs(shap_values).mean(0) # 对shap values按照特征维度聚合计算平均绝对值。
# feature_importance.sort_values('importance', ascending = False)  # 对 'importance' values 不升序排序并放入feature_importance。
# print(feature_importance) # 打印 feature_importance

shap.summary_plot（）的超参数：

shap_values ： 一个数组，其中包含了样本的 Shapley 值，大小为 [n_samples, n_features]
features ： 一个数组，其中包含了X_test所有值。需要与 shap_values 的样本数量一致。
feature_names： 特征名称列表，长度应该和 features 的列数相同。
max_display（default=all）：用于指定要显示的最多特征数量。
plot_type:  用于指定图形类型。可以设置为 ‘dot’ 或 ‘bar’。

4.5 蜂巢与特征重要性图结合

'''========================蜂巢与特征重要性图结合========================='''
# 创建主图（用来画蜂巢图）
fig, ax1 = plt.subplots()
# 在主图上绘制蜂巢图，并保留热度条
shap.summary_plot(shap_values, X_test, feature_names=columns,max_display = 25, plot_type="dot", show=False, color_bar=True)
plt.gca().set_position([0.2, 0.2, 0.65, 0.65])  # 调整图表位置，留出右侧空间放热度条
# 获取共享的 y 轴
ax1 = plt.gca()
# 创建共享 y 轴的另一个图，绘制特征贡献图在顶部x轴
ax2 = ax1.twiny()
shap.summary_plot(shap_values, X_test,feature_names=columns, max_display = 25,plot_type="bar", show=False)
plt.gca().set_position([0.2, 0.2, 0.65, 0.65])  # 调整图表位置，与蜂巢图对齐
# 在顶部 X 轴添加一条横线
ax2.axhline(y=25, color='gray', linestyle='-', linewidth=1)  # 注意y值应该对应顶部
# 调整透明度
bars = ax2.patches  # 获取所有的柱状图对象
for bar in bars:
    bar.set_alpha(0.3)# 设置透明度
# 设置两个x轴的标签
ax1.set_xlabel('Shapley Value Contribution (Bee Swarm)', fontsize=12)
ax2.set_xlabel('Mean Shapley Value (Feature Importance)', fontsize=12)
# 移动顶部的 X 轴，避免与底部 X 轴重叠
ax2.xaxis.set_label_position('top')  # 将标签移动到顶部
ax2.xaxis.tick_top()  # 将刻度也移动到顶部
# 设置y轴标签
ax1.set_ylabel('Features', fontsize=12)
plt.tight_layout()
plt.savefig("SHAP_combined_with_top_line_corrected.jpg", format='jpg', bbox_inches='tight')
plt.show()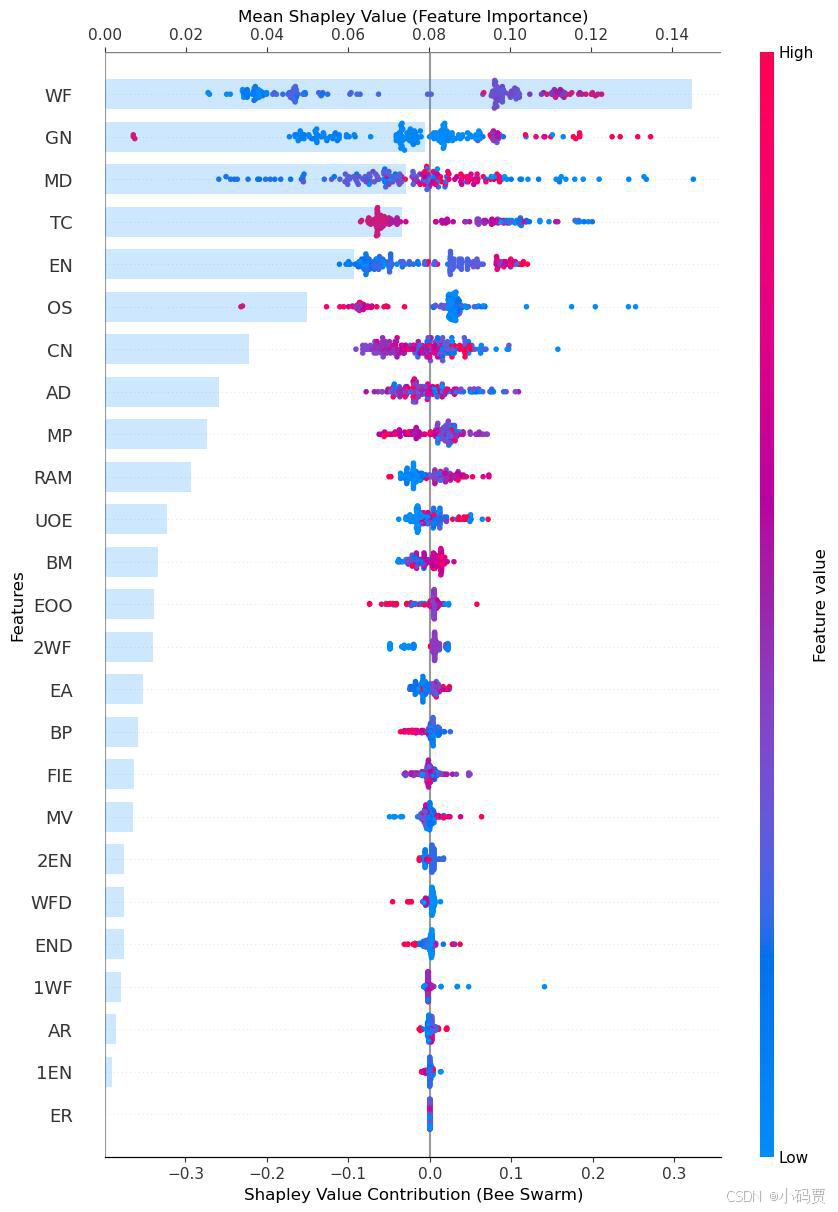

 五、代码全部注释

'''====================导入Python库===================='''
import pandas as pd               #python科学计算库
import numpy as np                #Python的一个开源数据分析处理库。
import matplotlib.pyplot as plt   #常用Python画图工具
from xgboost import XGBRegressor  # 导入 XGBRegressor 模型
from sklearn.model_selection import train_test_split # 数据划分模块
from sklearn.preprocessing import StandardScaler   # 标准化模块
from sklearn.metrics import mean_squared_error, r2_score   #误差函数MSE,误差函数R^2,
from sklearn.model_selection import GridSearchCV     #超参数网格搜索
import shap  # 导入SHAP模型解释工具


'''========================导入数据========================'''
data = pd.read_excel('D:/复现/trainset_loop6.xlsx')  #读取xlsx格式数据
# date = pd.read_csv('D:/复现/trainset_loop6.csv')   #读取csv格式数据
print(data.isnull().sum())   #检查数据中是否存在缺失值
print(data.shape)   #检查维度
print(data.columns) #数据的标签
data = data.drop(["PN","AN"], axis = 1) #axis = 1表示对列进行处理，0表示对行
Y, X = data['Eads'] , data.drop(['Eads'] , axis = 1) #对Y、X分别赋值
columns = X.columns


'''=========================标准化========================'''
#利用StandardScaler函数对X进行标准化处理
scaler = StandardScaler()
X = scaler.fit_transform(X)
'''====================划分训练集与测试集==================='''
X_train,X_test,y_train,y_test = train_test_split(X , Y , test_size=0.2 , random_state=42)



'''=======================模型训练========================'''
#模型训练
model = XGBRegressor()   # 模型实例化。
'''========================超参数========================='''
# booster: 默认值为 ‘gbtree’，基于树模型。 ‘gblinear’ 基于线性模型。
# silent: 默认为0；当这个参数值为1时，静默模式开启，不会输出任何信息。
# nthread：默认值为最大可能的线程数。
# eta: 权重递减参数，典型值为0.01-0.2。
# min_child_weight：决定最小叶子节点样本权重和。
# max_depth：这个值为树的最大深度。
# max_leaf_nodes：树上最大的节点或叶子的数量。
# gamma：Gamma指定了节点分裂所需的最小损失函数下降值。 这个参数的值越大，算法越保守。
# max_delta_step：每棵树权重改变的最大步长。如果这个参数的值为0，那就意味着没有约束。
# reg_alpha：权重的L1正则化项。 可以应用在很高维度的情况下，使得算法的速度更快。默认为1。
# reg_lambda：权重的L2正则化项。默认为1。
# colsample_bytree:  # 对特征随机采样的比例;如本文有25个特征,colsample_bytree=0.8,则为25*0.8=20。
# objective: 'reg:linear'线性回归,'reg:logistic'逻辑回归,'binary:logistic'二分类问题,'multi:softmax'多分类,用num_class指定类别数
# eval_metric: 评估指标,‘rmse’回归;‘mlogloss’多分类;‘error’二分类;‘auc’二分类任务。

# 定义超参数网格。
n_estimators = [100]  # 可以自己尝试添加参数；如：max_depth = [2,3,4,5,6]等。
max_depth = [3]
reg_alpha = [0.5]
reg_lambda = [0.5]

# min_samples_leaf = [1,3,5,7,9,11]  #有点费时间就没加这个超参数,想加的可以加,（不加可能会有点过拟合）。
# learning_rate = [0.1,0.5,1]  # 每棵树对最终预测的贡献,大的 learning_rate 能加快收敛速度，默认为0.1。
# 网格搜索,cv = 5 表示进行5折交叉验证
grid_search = GridSearchCV(estimator = model,cv = 5, param_grid={'max_depth': max_depth,"n_estimators":n_estimators,"reg_alpha":reg_alpha,"reg_lambda":reg_lambda}, scoring='neg_mean_squared_error')
grid_search.fit(X_train, y_train)
# 最佳模型
best_model = grid_search.best_estimator_
# 最佳超参数
best_max_depth = grid_search.best_params_['max_depth']
# best_min_samples_leaf = grid_search.best_params_['min_samples_leaf']
best_n_estimators = grid_search.best_params_['n_estimators']
best_reg_alpha = grid_search.best_params_['reg_alpha']
best_reg_lambda = grid_search.best_params_['reg_lambda']
print(f'Best max_depth:{best_max_depth:.3f}',"\n",f'Best n_estimators:{best_n_estimators:.3f}',  # ,"\n",用于换行
      "\n",f'Best reg_alpha:{best_reg_alpha:.3f}',"\n",f'Best reg_lambda:{best_reg_lambda:.3f}')


'''=====================SHAP解释模型======================'''
explainer = shap.TreeExplainer(best_model)  # 传入训练好的模型。
shap_values = explainer.shap_values(X_test)  # 这里拿验证数据集进行呈现。输入X_train拿训练数据集进行呈现。


#summary plot是针对全部样本预测的解释，有两种图，‘bar’一种是取每个特征的shap values的平均绝对值来获得标准条形图，这个其实就是全局重要度，
# ‘dot’另一种是通过散点简单绘制每个样本的每个特征的shap values，通过颜色可以看到特征值大小与预测影响之间的关系，同时展示其特征值分布。
'''=====================SHAP值特征贡献的蜂巢图（'dot'）======================'''
plt.figure()  # figsize=(10, 5)设置图的大小，dpi=1200 像素大小。
shap.summary_plot(shap_values = shap_values,  # 一个数组，其中包含了样本的 Shapley 值，大小为 [n_samples, n_features]
                  features = X_test , # 一个数组，其中包含了样本的特征矩阵。这需要与 shap_values 中的样本数量一致。
                  feature_names = columns, # 特征名称列表，长度应该和 features 的列数相同。
                  max_display = 25,    # 可选参数，用于指定要显示的最多特征数量。默认情况下，将显示所有特征。
                  plot_type = "dot",  # 可选参数，用于指定图形类型。可以设置为 ‘dot’ 或 ‘bar’。
                  show=False   # 不展示
                  )
plt.savefig("SHAP_numpy summary_plot.jpg", format='jpg',bbox_inches='tight') # 图保存为pdf格式
plt.show()  # 展示

'''=====================SHAP值特征贡献的蜂巢图（'dot'）======================'''
plt.figure()
shap.summary_plot(shap_values = shap_values,  # 一个数组，其中包含了样本的 Shapley 值，大小为 [n_samples, n_features]
                  features = X_test , # 一个数组，其中包含了样本的特征矩阵。这需要与 shap_values 中的样本数量一致。
                  feature_names = columns, # 特征名称列表，长度应该和 features 的列数相同。
                  max_display = 25,    # 可选参数，用于指定要显示的最多特征数量。默认情况下，将显示所有特征。
                  plot_type = "bar",  # 可选参数，用于指定图形类型。可以设置为 ‘dot’ 或 ‘bar’。
                  show=False   # 不展示
                  )
plt.title('SHAP_numpy Sorted Feature Importance')  # 标题名称
plt.tight_layout()  # 显示标题
plt.savefig("SHAP_numpy Sorted Feature Importance.jpg", format='jpg',bbox_inches='tight') # 图保存为pdf格式
plt.show()  # 展示

'''=====================打印feature_importance值======================'''
# feature_importance = pd.DataFrame()  #创建一个 DataFrame 来存储 feature_importance。
# feature_importance['feature'] = columns  # 给 'feature' 赋予特征名称。
# feature_importance['importance'] = np.abs(shap_values).mean(0) # 对shap values按照特征维度聚合计算平均绝对值。
# feature_importance.sort_values('importance', ascending = False)  # 对 'importance' values 不升序排序并放入feature_importance。
# print(feature_importance) # 打印 feature_importance

'''========================蜂巢与特征重要性图结合========================='''
# 创建主图（用来画蜂巢图）
fig, ax1 = plt.subplots()
# 在主图上绘制蜂巢图，并保留热度条
shap.summary_plot(shap_values, X_test, feature_names=columns,max_display = 25, plot_type="dot", show=False, color_bar=True)
plt.gca().set_position([0.2, 0.2, 0.65, 0.65])  # 调整图表位置，留出右侧空间放热度条
# 获取共享的 y 轴
ax1 = plt.gca()
# 创建共享 y 轴的另一个图，绘制特征贡献图在顶部x轴
ax2 = ax1.twiny()
shap.summary_plot(shap_values, X_test,feature_names=columns, max_display = 25,plot_type="bar", show=False)
plt.gca().set_position([0.2, 0.2, 0.65, 0.65])  # 调整图表位置，与蜂巢图对齐
# 在顶部 X 轴添加一条横线
ax2.axhline(y=25, color='gray', linestyle='-', linewidth=1)  # 注意y值应该对应顶部
# 调整透明度
bars = ax2.patches  # 获取所有的柱状图对象
for bar in bars:
    bar.set_alpha(0.3)# 设置透明度
# 设置两个x轴的标签
ax1.set_xlabel('Shapley Value Contribution (Bee Swarm)', fontsize=12)
ax2.set_xlabel('Mean Shapley Value (Feature Importance)', fontsize=12)
# 移动顶部的 X 轴，避免与底部 X 轴重叠
ax2.xaxis.set_label_position('top')  # 将标签移动到顶部
ax2.xaxis.tick_top()  # 将刻度也移动到顶部
# 设置y轴标签
ax1.set_ylabel('Features', fontsize=12)
plt.tight_layout()
plt.savefig("SHAP_combined_with_top_line_corrected.jpg", format='jpg', bbox_inches='tight')
plt.show()

参考链接：

• Welcome to the SHAP documentation — SHAP latest documentation

• 机器学习模型可解释性

• Exercise: Advanced Uses of SHAP Values | Kaggle

持续更新中。。。