一、论文介绍
镁 (Mg) 合金具有重量轻和生物相容性强的特点,可广泛应用于运输、航空航天和生物医学领域。然而,由于高化学活性,它们通常会受到严重的电偶腐蚀。在这项工作中,采用主动学习来发现 可以抑制 Mg 合金腐蚀阴极反应的金属间化合物。氢吸附能是阴极析氢反应 (HER) 速率的描述符,由机器学习模型使用 H 原子的 Voronoi 邻居的几何和化学特征进行预测。经过五次主动学习迭代后,在训练集大小小于 1% 未知数据集的情况下,强/弱吸附配置的 H 吸附能量预测误差为 0.196 eV (MAE)。此外,我们发现具有强 H 吸附的表面比弱 H 吸附表面向 H 吸附原子转移的电子更多。最后,根据二元 Mg 金属间化合物的表面稳定性和预测的 H 吸附能对二元 Mg 金属间化合物抑制 HER 的能力进行排序。这项工作通过主动学习和密度泛函理论 (DFT) 模拟提出了可以极大地抑制腐蚀阴极反应的二元 Mg 金属间化合物,有望加速耐腐蚀 Mg 合金的设计。
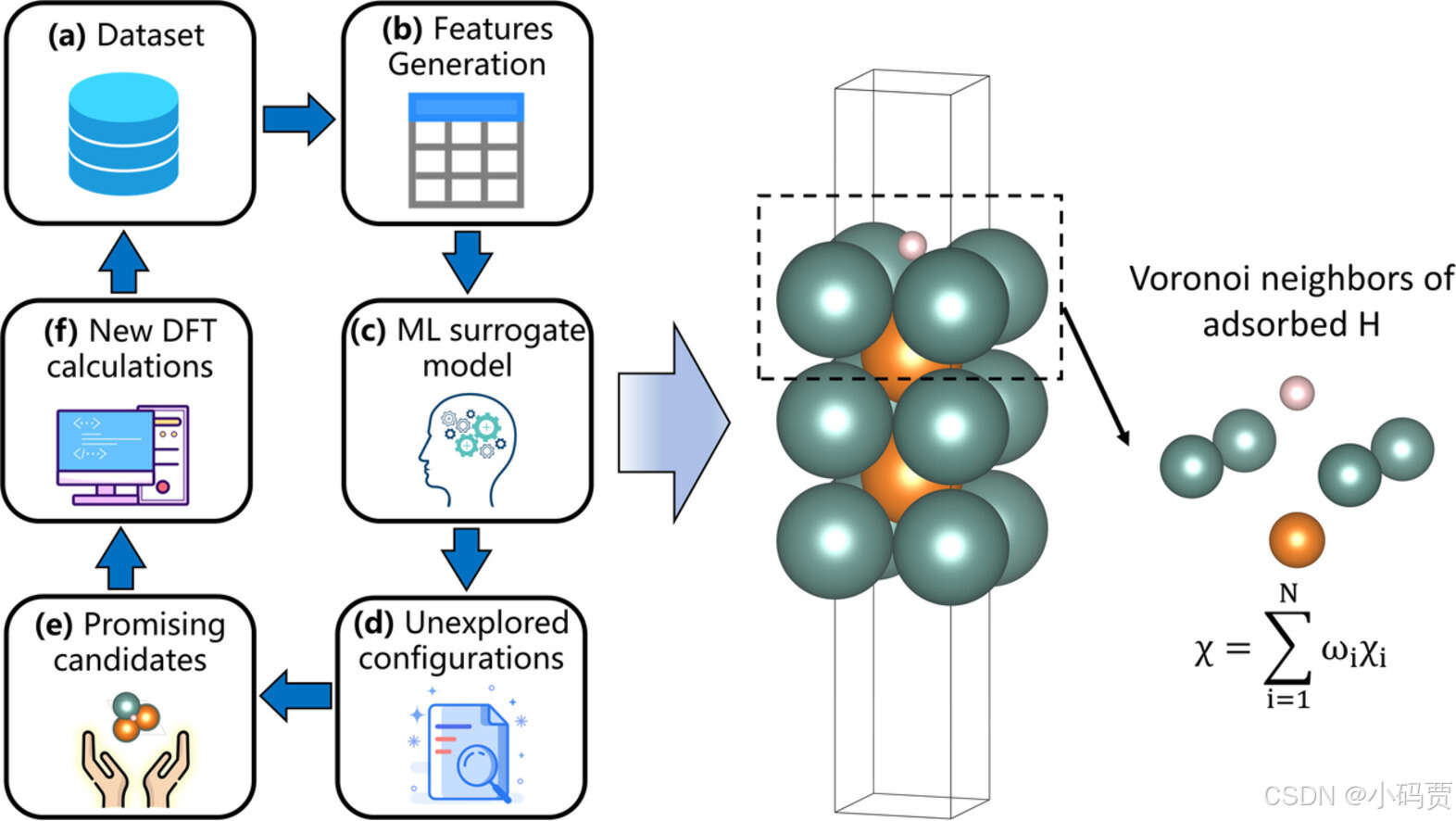
图片来自 https://doi.org/10.1016/j.actamat.2023.119063
(a) 原始数据集(b)有效特征提取(c) ML(Machine Learning)模型训练。(d)提取结构特征(未被计算过的结构)(e)ML 模型预测的有效结果(f) 根据预测的有效结构进行 DFT 计算,得到 数据添加到数据集中。不断循环此过程,模型越来越强大。
二、数据集
其初始数据为690*27(690个结构,27个特征),通过 Pearson 相关系数 (PCC) 考虑特征的相关性后,由于与其他特征的高线性关系,排除了 2 个特征。即690*25的数据经过5次上述主动学习迭代过程得到最后数据集最后数据集。(890*25)
三、模型训练
3.1 导入Python库
'''====================导入Python库===================='''
import pandas as pd #python科学计算库
import numpy as np #Python的一个开源数据分析处理库。#
import matplotlib.pyplot as plt #常用Python画图工具
import seaborn as sns #基于 Matplotlib 的 Python 数据可视化库,专注于绘制各种统计图形,提供高级接口和美观的默认主题。
import mglearn #用于辅助机器学习和数据分析的工具包。它提供了一些方便的函数和工具,帮助用户更好地理解和应用机器学习算法。mglearn的目标是简化机器学习的学习曲线,让初学者更容易上手。
from sklearn.linear_model import LinearRegression # 线性回归模型
from sklearn.model_selection import train_test_split # 数据划分模块
from sklearn.preprocessing import StandardScaler # 标准化模块
from sklearn.metrics import mean_squared_error,r2_score #误差函数MSE,误差函数R^2,首先,导入一些常用的Python库:
pandas: Pandas是Python的一个开源数据分析处理库。它提供了高性能易用的数据结构和数据分析工具,用于进行数据的读取、清洗、过滤、聚合、视觉化等操作。
numpy: python科学计算库,提供了矩阵,线性代数,傅立叶变换等等的解决方案, 最常用的是它的N维数组对象。
scikit-learn: 是基于 Python 语言的机器学习工具。有六大任务模块:分别是分类、回归、聚类、降维、模型选择和预处理。
3.2 导入数据
'''========================导入数据========================'''
data = pd.read_excel('D:/复现/trainset_loop6.xlsx') #读取xlsx格式数据
# date = pd.read_csv('D:/复现/trainset_loop6.csv') #读取csv格式数据
print(data.isnull().sum()) #检查数据中是否存在缺失值
print(data.shape) #检查维度
print(data.columns) #数据的标签
data = data.drop(["PN","AN"], axis = 1) #axis = 1表示对列进行处理,0表示对行
Y, X = data['Eads'] , data.drop(['Eads'] , axis = 1) #对Y、X分别赋值3.3 分析数据分布
'''===================data数据结构可视化==================='''
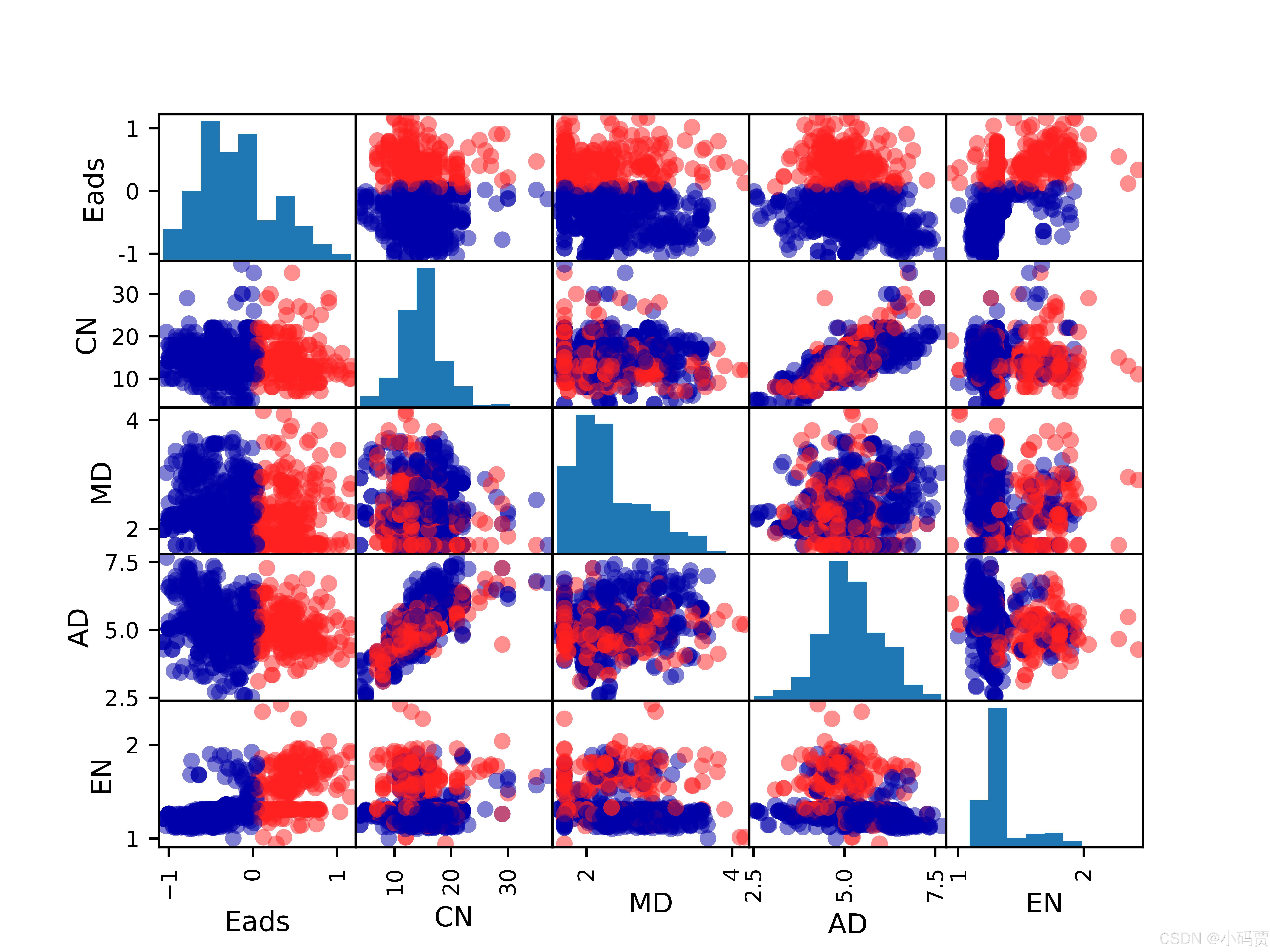
#scatter_matrix函数,它会绘制出每个数值属性相对于其他数值属性的相关值。
pd.plotting.scatter_matrix(data.iloc[:,0:5], # pandas.dataframe对象,这里导入了data的前5列进行分析。
alpha = 0.5 , #图像透明度,一般取(0, 1]
figsize = (10,10), #以英寸为单位的图像大小,一般以元组(width, height)
diagonal = 'hist', #’hist’表示直方图(Histogramplot), ’kde’表示核密度估计;该参数是scatter_matrix函数的关键参数
hist_kwds = {'bins': 10},#与hist相关的字典参数
marker = 'o', #Matplotlib可用的标记类型,如’.’,’, ’,’o’等
c = Y , #颜色参考标准
cmap = mglearn.cm2) #两特征的颜色分布
# 将图保存为*.jpg图
plt.savefig('./data_Distribute.jpg',dpi = 1200) #在当前文件夹下保存jpg格式图,dpi = 1200
plt.show()
3.4 Pearson 相关性分析
'''===================Pearson 相关性分析==================='''
# 计算相关系数矩阵,包含了任意两个data特征的相关系数
print(data.corr())
# 绘制相关性热力图
plt.subplots() # 设置画面大小,如:figsize = (8, 8)
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
sns.heatmap(data.corr(), #要分析的数据,这里放入了data的特征的相关系数
annot=False, # 显示相关系数
center=0.5, # 居中
fmt='.2f', # 只显示一位小数
linewidth=0.5, # 设置每个单元格的距离
linecolor='black', # 设置间距线的颜色
vmin=0, vmax=1, # 设置数值最小值和最大值
xticklabels=True, yticklabels=True, # 显示x轴和y轴
square=True, # 每个方格都是正方形
cbar=True, # 绘制颜色条
cmap='coolwarm', # 设置热力图颜色
)
plt.title('相关性热力图') #图的标题
# 将图保存为*.jpg图
plt.savefig('./Pearson_Picture.jpg',dpi = 1200) #在当前文件夹下保存jpg格式图,dpi = 1200
plt.show()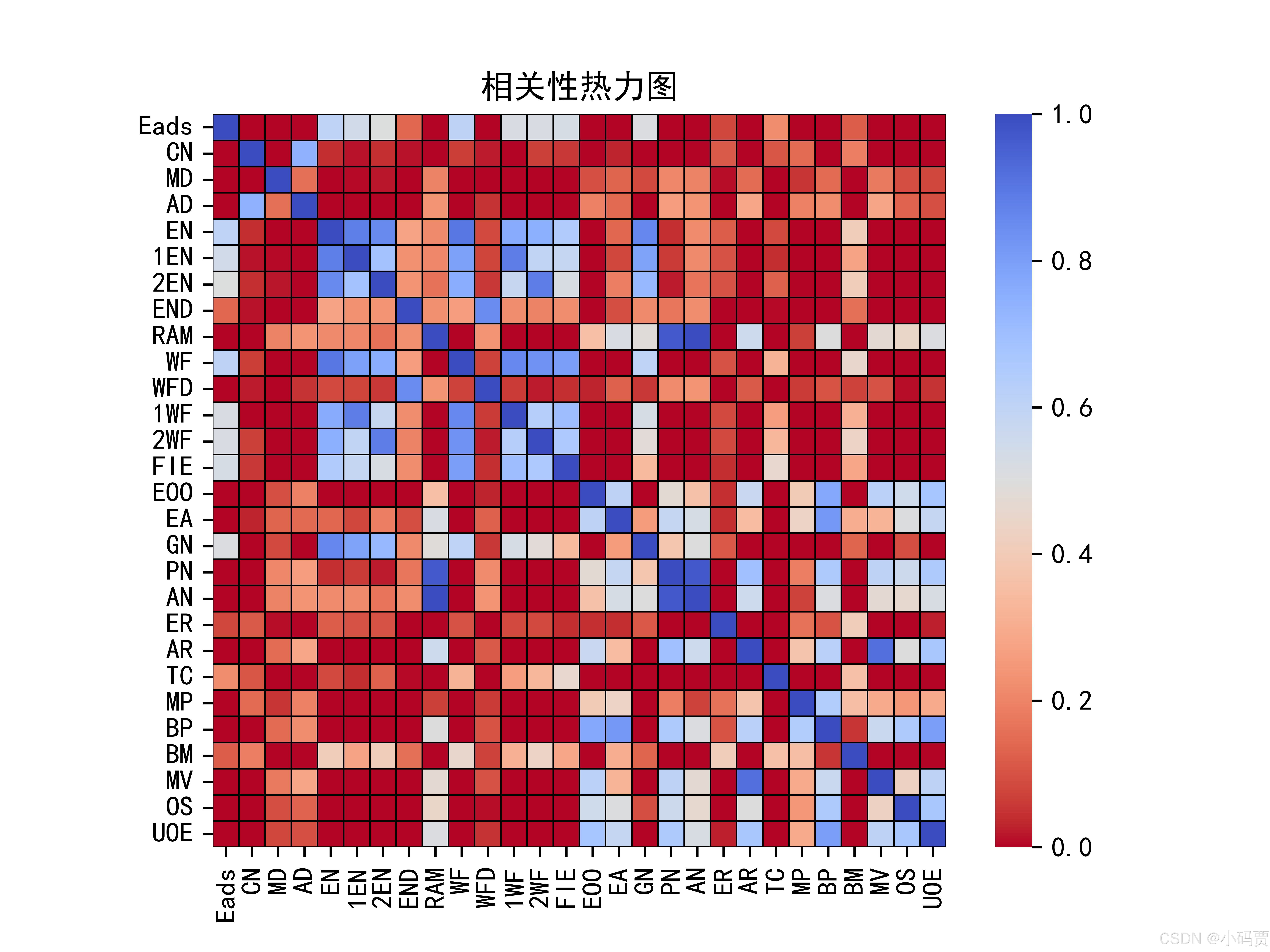
作者去除相关性大的 "PN" 和 "AN" 特征
data = data.drop(['PN', 'AN'],axis = 1) #axis = 1表示对列进行处理,0表示对行3.5 标准化
'''=========================标准化========================'''
#利用StandardScaler函数对X进行标准化处理
scaler = StandardScaler()
X = scaler.fit_transform(X)
'''====================划分训练集与测试集==================='''
X_train,X_test,y_train,y_test = train_test_split(X,Y,test_size=0.2,random_state=42)3.6 模型训练与评估
'''=====================模型训练与评估======================'''
#模型训练
model = LinearRegression() # LinearRegression模型实例化
model.fit(X_train,y_train) # 利用训练集进行模型训练
#模型预测
y_pred_train=model.predict(X_train) # 利用训练集进行模型预测
y_pred_test=model.predict(X_test) # 利用预测集进行模型预测
#评估
mse_train=mean_squared_error(y_train,y_pred_train) #均方误差越小模型越好
mse_test=mean_squared_error(y_test,y_pred_test) #R2 表示模型对因变量的解释能力,取值范围从 0 ~ 1,越接近 1 表示模型对数据的拟合程度越好。
r2_train=r2_score(y_train,y_pred_train)
r2_test=r2_score(y_test,y_pred_test)
print(f'MSE(Train):{mse_train:.2f}') #保留2位小数
print(f'MSE(Test):{mse_test:.2f}')
print(f'R^2(Train):{r2_train:.2f}')
print(f'R^2(Test):{r2_test:.2f}')
'''=====================特征权重Wi图======================'''
plt.bar(columns, model.coef_) # X轴columns特征名;Y轴model.coef_模型输出的Wi
plt.title('Linear Regression 预测的各特征权重W$_i$')
plt.savefig('./LR_Wi.jpg',dpi = 1200) #在当前文件夹下保存jpg格式图,dpi = 1200
plt.show() MSE与结果:
MSE(Train):0.10
MSE(Test):0.09
R^2(Train):0.53
R^2(Test):0.49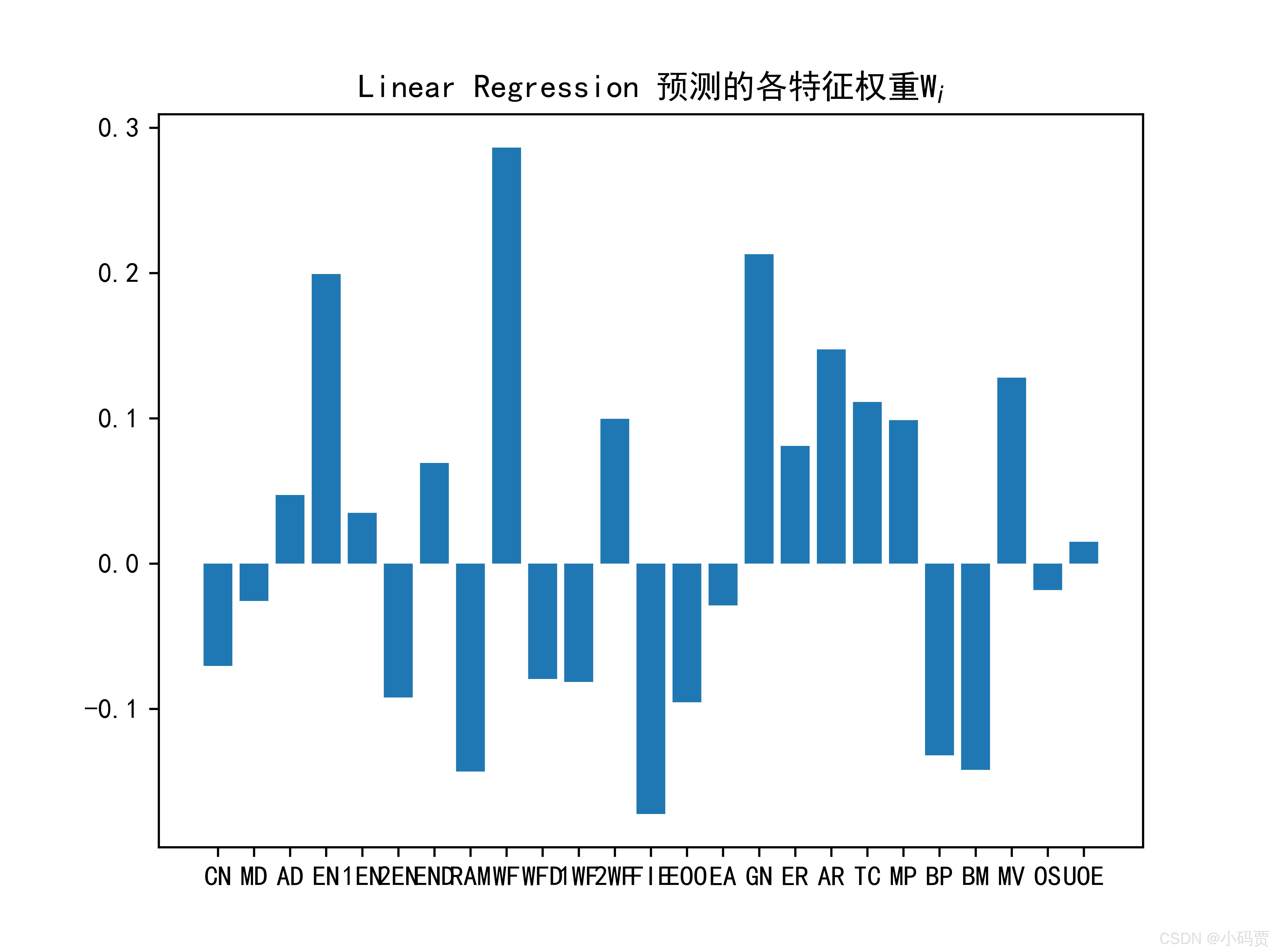
3.7 可视化
'''======================结果可视化======================='''
plt.figure(figsize=(8,8))
colors = ['b', 'r'] # 设置颜色
markers = ["*","o"] # 设置点的形状
Y_train_picture = [y_train,y_test] #可视化图的x轴数据
Y_pred_picture = [y_pred_train,y_pred_test] #可视化图的y轴数据
for i in range(0,2):
plt.scatter(Y_train_picture[i],
Y_pred_picture[i],
s = 20, # 表示点的大小
c = colors[i], # 颜色
marker = markers[i], # 点的形状
edgecolors='b', # 散点边框颜色
alpha=0.6) # 透明度
plt.plot([-1.0,1.0],[-1.0,1.0],'r--') #可视化图数据范围
plt.xlabel('Actual') #x轴标签
plt.ylabel('Predicted') #y轴标签
plt.legend(['train', 'test'], loc='upper right',frameon=False) #图例,位置位于右上方,去掉图例边框
plt.title('Actual vs Predicted',fontsize=15, c='r')
# 将图保存为*.jpg图
plt.savefig('./LR可视化_Picture.jpg',dpi = 1200) #在当前文件夹下保存jpg格式图,dpi = 1200
plt.show()
此图表示,数据点越靠近中间红线模型越好。
四、代码全部注释
'''====================导入Python库===================='''
import pandas as pd #python科学计算库
import numpy as np #Python的一个开源数据分析处理库。#
import matplotlib.pyplot as plt #常用Python画图工具
import seaborn as sns #基于 Matplotlib 的 Python 数据可视化库,专注于绘制各种统计图形,提供高级接口和美观的默认主题。
import mglearn #用于辅助机器学习和数据分析的工具包。它提供了一些方便的函数和工具,帮助用户更好地理解和应用机器学习算法。mglearn的目标是简化机器学习的学习曲线,让初学者更容易上手。
from sklearn.linear_model import LinearRegression # 线性回归模型
from sklearn.model_selection import train_test_split # 数据划分模块
from sklearn.preprocessing import StandardScaler # 标准化模块
from sklearn.metrics import mean_squared_error,r2_score #误差函数MSE,误差函数R^2,
'''========================导入数据========================'''
data = pd.read_excel('D:/复现/trainset_loop6.xlsx') #读取xlsx格式数据
# date = pd.read_csv('D:/复现/trainset_loop6.csv') #读取csv格式数据
print(data.isnull().sum()) #检查数据中是否存在缺失值
print(data.shape) #检查维度
print(data.columns) #数据的标签
data = data.drop(["PN","AN"], axis = 1) #axis = 1表示对列进行处理,0表示对行
Y, X = data['Eads'] , data.drop(['Eads'] , axis = 1) #对Y、X分别赋值
columns = X.columns #用于后续画特征权重图
'''===================data数据结构可视化==================='''
#scatter_matrix函数,它会绘制出每个数值属性相对于其他数值属性的相关值。
pd.plotting.scatter_matrix(data.iloc[:,0:5], # pandas.dataframe对象,这里导入了data的前5列进行分析。
alpha = 0.5 , #图像透明度,一般取(0, 1]
figsize = (10,10), #以英寸为单位的图像大小,一般以元组(width, height)
diagonal = 'hist', #’hist’表示直方图(Histogramplot), ’kde’表示核密度估计;该参数是scatter_matrix函数的关键参数
hist_kwds = {'bins': 10},#与hist相关的字典参数
marker = 'o', #Matplotlib可用的标记类型,如’.’,’, ’,’o’等
c = Y , #颜色参考标准
cmap = mglearn.cm2) #两特征的颜色分布
# 将图保存为*.jpg图
plt.savefig('./data_Distribute.jpg',dpi = 1200) #在当前文件夹下保存jpg格式图,dpi = 1200
plt.show()
'''===================Pearson 相关性分析==================='''
# 计算相关系数矩阵,包含了任意两个data特征的相关系数
print(data.corr())
# 绘制相关性热力图
plt.subplots() # 设置画面大小,如:figsize = (8, 8)
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
sns.heatmap(data.corr(), #要分析的数据,这里放入了data的特征的相关系数
annot=False, # 显示相关系数
center=0.5, # 居中
fmt='.2f', # 只显示一位小数
linewidth=0.5, # 设置每个单元格的距离
linecolor='black', # 设置间距线的颜色
vmin=0, vmax=1, # 设置数值最小值和最大值
xticklabels=True, yticklabels=True, # 显示x轴和y轴
square=True, # 每个方格都是正方形
cbar=True, # 绘制颜色条
cmap='coolwarm', # 设置热力图颜色
)
plt.title('相关性热力图') #图的标题
# 将图保存为*.jpg图
plt.savefig('./Pearson_Picture.jpg',dpi = 1200) #在当前文件夹下保存jpg格式图,dpi = 1200
plt.show()
'''=========================标准化========================'''
#利用StandardScaler函数对X进行标准化处理
scaler = StandardScaler()
X = scaler.fit_transform(X)
'''====================划分训练集与测试集==================='''
X_train,X_test,y_train,y_test = train_test_split(X,Y,test_size=0.2,random_state=42)
'''=====================模型训练与评估======================'''
#模型训练
model = LinearRegression() # LinearRegression模型实例化
model.fit(X_train,y_train) # 利用训练集进行模型训练
#模型预测
y_pred_train=model.predict(X_train) # 利用训练集进行模型预测
y_pred_test=model.predict(X_test) # 利用预测集进行模型预测
#评估
mse_train=mean_squared_error(y_train,y_pred_train) #均方误差越小模型越好
mse_test=mean_squared_error(y_test,y_pred_test) #R2 表示模型对因变量的解释能力,取值范围从 0 ~ 1,越接近 1 表示模型对数据的拟合程度越好。
r2_train=r2_score(y_train,y_pred_train)
r2_test=r2_score(y_test,y_pred_test)
print(f'MSE(Train):{mse_train:.2f}') #保留2位小数
print(f'MSE(Test):{mse_test:.2f}')
print(f'R^2(Train):{r2_train:.2f}')
print(f'R^2(Test):{r2_test:.2f}')
'''=====================特征权重Wi图======================'''
plt.bar(columns, model.coef_) # X轴columns特征名;Y轴model.coef_模型输出的Wi
plt.title('Linear Regression 预测的各特征权重W$_i$')
plt.savefig('./LR_Wi.jpg',dpi = 1200) #在当前文件夹下保存jpg格式图,dpi = 1200
plt.show()
'''======================结果可视化======================='''
plt.figure(figsize=(8,8))
colors = ['b', 'r'] # 设置颜色
markers = ["*","o"] # 设置点的形状
Y_train_picture = [y_train,y_test] #可视化图的x轴数据
Y_pred_picture = [y_pred_train,y_pred_test] #可视化图的y轴数据
for i in range(0,2):
plt.scatter(Y_train_picture[i],
Y_pred_picture[i],
s = 20, # 表示点的大小
c = colors[i], # 颜色
marker = markers[i], # 点的形状
edgecolors='b', # 散点边框颜色
alpha=0.6) # 透明度
plt.plot([-1.0,1.0],[-1.0,1.0],'r--') #可视化图数据范围
plt.xlabel('Actual') #x轴标签
plt.ylabel('Predicted') #y轴标签
plt.legend(['train', 'test'], loc='upper right',frameon=False) #图例,位置位于右上方,去掉图例边框
plt.title('Actual vs Predicted',fontsize=15, c='r')
# 将图保存为*.jpg图
plt.savefig('./LR可视化_Picture.jpg',dpi = 1200) #在当前文件夹下保存jpg格式图,dpi = 1200
plt.show()
其中,有几个点,需要大家注意下~
-
数据预处理:确保所有特征进行标准化,避免特征值差异过大对模型的影响。
-
特征重要性:LinearRegression 回归会输出模型各特征的权重,可以查看哪些特征对模型的贡献最大,这也可以帮助我们理解特征的重要性。
-
模型评估:计算 MSE 和 R² 来评估模型性能,并通过可视化检查预测效果。























 945
945

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










