《高频电子线路》 —— 单级高频谐振小信号放大器的增益

膝盖中箭卫兵

已于 2024-11-04 13:31:00 修改

阅读量1.8k

点赞数 15

分类专栏：【通信(高频)电子线路精品公开课—中国MOOC】笔记分享文章标签：笔记

于 2024-10-28 16:42:14 首次发布

本文链接：https://blog.csdn.net/2301_79288228/article/details/143302480

版权

【通信(高频)电子线路精品公开课—中国MOOC】笔记分享专栏收录该内容

32 篇文章

订阅专栏

文章内容来源于【中国大学MOOC 华中科技大学通信（高频）电子线路精品公开课】，此篇文章仅作为笔记分享。

单级高频谐振小信号放大器

对于给定的电路，先画出其高频交流等效电路，然后求其增益、通频带和选择性。

将电路一分为二，右上部分，是带抽头的并联谐振回路，左下部分，就是晶体管的放大电路。
晶体管放大电路的静态工作点由R1、R2、R3决定。
C3代表发射极的旁路电容，对于电源而言，负极供电，LF和CF是滤波电路。

高频交流等效电路

其中Y参数等效电路代表着晶体管，带抽头的是并联谐振回路的等效电路。
其中gp是并联谐振回路的谐振电阻Rp的倒数，Rp实际上是电感的损耗电阻R，R原本是与电感串联的形式，为了计算方便，将其转化成了并联的形式，在并联的形式中是以电导的形式体现的。
在原始的电路里，是没有Rp的，Rp只会出现在等效电路中，必须要小心，避免在并联谐振等效回路中遗漏Rp。
有了这两个部分后，在加上信号源以及信号源的导纳和负载导纳即可（此处的负载假设的是下一级是采用晶体管的放大器，下一级晶体管的输入导纳，即为本级的负载导纳）。

电压增益

要求电压增益，需要求出输出电压和输入电压的关系。
首先需要建立输入电压Vi和集电极电压Vc之间的关系，是通过外参数来建立。
其次再通过抽头之间的关系来建立集电极电压Vc和输出电压Vo之间的关系。

Vi与Vc之间的关系

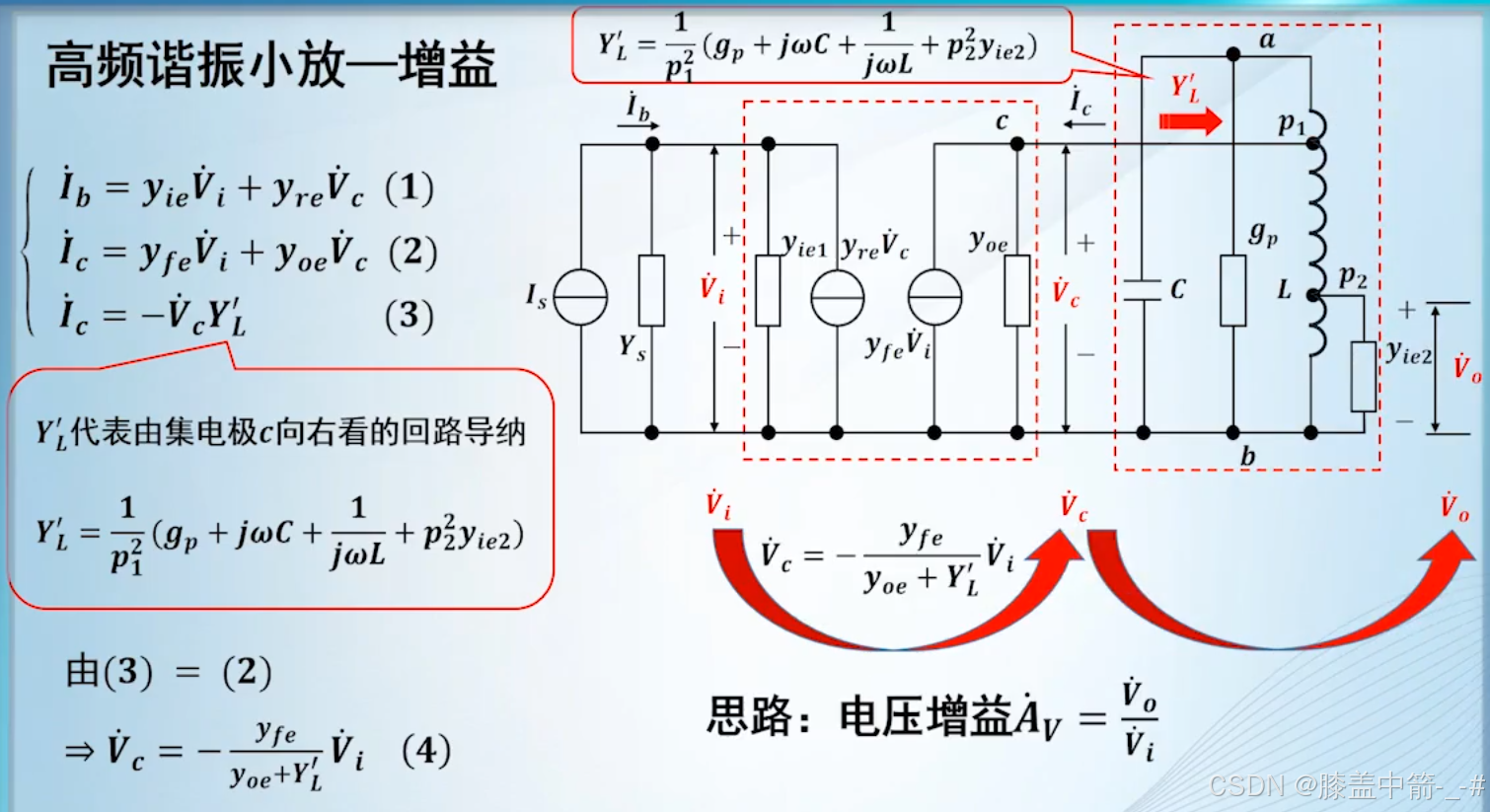
根据外参数的电流Ib，可以建立方程一：
根据外参数电流的Ic，可以建立方程二：
再根据集电极电流Ic流向抽头，可以得到方程三：
其中Y'L表示集电极C向右看过去的回路导纳。

集电极C向右看过去的回路导纳Y'L，包括四部分：
：并联谐振回路的电阻。
：并联谐振回路的电容。
：并联谐振回路的电感。
:负载折合过来的导纳。

再根据第三个式子和第二个式子相等联立，就可以得到Vc和Vi之间的关系：

注意：yf1代表的是晶体管的放大倍数。

Vc与Vo之间的关系

Vc电压过来是接到抽头p1，输出电压Vo是以抽头p2接入的。
所以根据抽头的电压变化比，就可以得到Vc与Vo之间的关系。

计算电压增益

代入Vo、Vc、Y'L

把输出电压Vo代入，再把Vc的电压代入，再把Y'L代入，就得到了这样一个复杂的式子。

分析一下分母的物理意义：
从左到右分别代表：信号源折合过来的导纳、并列谐振的电阻、并列谐振的电容、并列谐振的电感和负载折合过来的导纳。正好就是并联谐振回路的左边和右边。

拆解yoe、yie2

进一步的把yoe拆解成电导和电纳：
进一步的把yie2拆解成电导和电纳：
因为yoe和yie2都是放大管等效出来的，没有电感的成分，只有电容的成分。

整理式子的分母

再整理一下分母得到：

将所有的电电导整合到一起，称为g∑；
所有的电容整合到一起，称为C∑；
最后把所有电感放到一起。

电压增益的最简式

最后就可以得到电压增益较为简洁的式子：

分母里包括三大块：电导（电阻成分）、容抗（电容成分）、感抗（电感成分）。
yf1代表着晶体管的放大倍数，对高频谐振小信号放大电路的电压增益起到决定性的作用。
负号代表着输入和输出信号相位正好相反，因为正好是共射极放大电路。

说明g∑和C∑的使用

以g∑为例，从刚才的推导中可以看到它包括三项，中间一项代表着并联谐振回路的电导，右边一项代表着负载折合过来的电导，左边一项代表着左边信号源折合过来的电导。但是g∑不一定永远等于这三项。
假如在并联谐振回路中增加了电阻R4，那么相应的高频交流等效电流就会发生改变，随之g∑也会有相应的增减，那么针对R4的增加，需要在g∑中对应增大电导g4，是电阻R4的倒数。