目录
摘要
在本周中,通过阅读文献,进一步了解了使用域分解PINN来解决问题的适用情况以及其原理和优劣性,具体做法为:每个子域使用单独的PINN来计算局部解,通过在接口处施加额外的连续性条件来无缝连接。且可以通过研究各界面上的各种连续条件用于提高性能。在Fluent中,选用径向流入的穿孔管道分析分析,进行几何划分和设置求解。理论学习方面,对有限体积法的基本原理进行了学习。
Abstract
This week, I read the literature to learn more about the applicability and pros and cons of using domain decomposition PINNs to solve problems by using a separate PINN for each subdomain to compute a local solution, seamlessly connected by imposing additional continuity conditions at the interface. It can also be used to improve performance by studying various continuous conditions on various surfaces. In Fluent, I used a radial inflow perforated pipe analysis to do the geometry and setup solving. In terms of theoretical study, I learned the basic principles of the finite volume method.
文献阅读:使用带有域分解的PINN求解NS方程
文献摘要
本文通过使用域分解的PINN来求解NS方程,并评估了该方法的准确性,收敛性以及不同策略对预测性能的影响。具体做法为:每个子域使用单独的PINN来计算局部解,通过在接口处施加额外的连续性条件来无缝连接。且可以通过研究各界面上的各种连续条件用于提高性能。
文中从流体力学和生物流体力学中的经典问题,包括:二维 Kovasznay流、三维Beltrami流、二维盖驱动腔流和二维圆柱体尾流,以及血管3D血液流动模拟来研究域分解PINN方来求解NS方程,实验结果证明了区域分解PINN方法在精确求解不可压缩Navier-Stokes流问题方面的能力和通用性。
文献讨论|结论
文中从以下观点中提出了PINN的优劣势:
- 传统的数值方法(CFD)面临着诸如复杂的计算机代码、解决所有物理尺度所需的高计算成本以及参数值的不确定性的挑战,而PINN可以以更高的效率和准确性处理复杂流体流动模拟的能力。
- 对当前深度学习算法(包括pinn)的一个重要评判是围绕它们的可解释性和理论收敛性,而这些仍然没有得到充分的理论证实。
- 域分解方式的PINN除了增强并行化能力外,还具有提高精度的优点:通过使用单独的神经网络来学习每个子域内的子问题;并且加入连续性条件(残差连续性条件,通量连续性和高阶连续性条件),该策略可以在几个关键方面显著提高准确性。
文献通过观察诸如精度,收敛性以及各种策略的影响等因素,在界面上引入了创新的连续性条件,如残差和通量连续性,并分析了它们对预测精度和界面一致性的影响。并提出动态权重法和结合注意机制的神经网络架构,意在解决在域分解PINN方法中经常遇到的梯度病理问题。
在对子域的处理中,我们在每个子域中使用单独的网络,为并行计算提供了一个简单的应用;然而,没有探讨分布式系统实现的细节或并行效率。
通过实验验证有如下结论:
- 观察到界面上的连续性条件显著提高了界面的连续性和预测精度。
- 网络结构中的动态权重策略和注意机制有助于提高预测精度。这些方法促进了梯度更一致的行为,增强了整体的平衡、稳定性和收敛速度。
- 没有深入研究该方法在分布式系统上的具体实现或该方法的并行效率。在今后的工作中探索该方法的并行计算前景是很有意义的。
- 认识到在相应的子领域中采用适当设置配置的潜力,包括网络体系结构、优化方法和训练点。这些进展将进一步提高区域分解PINN方法的性能和适应性。
- 在PINN中专门学习PDE的特定实例的解函数,缺乏在不重新优化的情况下推广到其他实例的能力。例如,当使用特定雷诺数下的观测数据训练PINN模型时,除非模型经过重新优化,否则它可能无法准确预测不同雷诺数下的流动。
实验设置
NS方程介绍
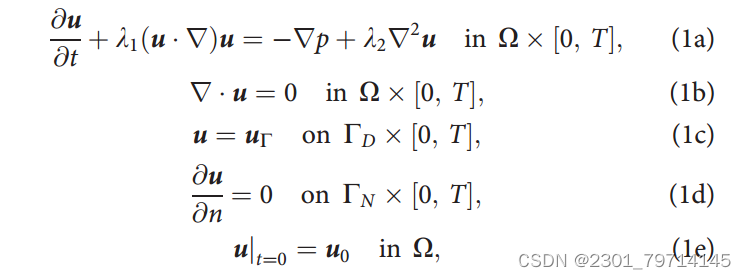
如图所示,本次实验中的NS方程如下设置,其中T为模拟的实践周期,u为速度矢量场,λ为流体性质,式(1a)对应动量守恒,式(1b)对应质量守恒。此外,方程式。(1c)和(1d)描述边界条件,(1e)是初始条件。
PINN框架
设uNN为由L个隐藏层组成的前馈神经网络,如图所示:

也可表示为:
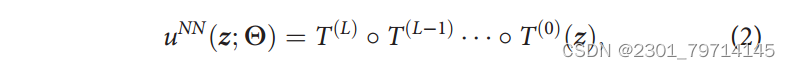
其中:∘为各种函数的组合;T为第i层的映射,其中的z为(i-1)输出向量;也为第i层的输入向量,表示为:
W为权重矩阵,b为偏置向








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 380
380

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








