同相放大器和同相积分运算放大器

前言

        节后的第一周，不知道大家的元旦过得怎么样呢，假期有没有去感受一下诗和远方2333。前两期的内容和大家分享了反相放大电路和从反相放大展开的T型网络反相比例运算电路和反相积分运算电路。笔者写csdn的逻辑是先介绍反相一类及其延伸，再介绍同相一类，后面还会再补充同相和反相的加减法等运算电路。话不多说，今天分享的第三期是同相放大电路和同相积分放大电路。 

1.同相放大器电路

1.1 同相放大器电路图

1.2 同相放大器电路分析

        1.“虚短”，“虚断”可以得到：Up = Un = Ui，ip = in = 0，这里有一个点是从初学者过来的我给大家提的一个小tips吧，不能上来就想当然的认为虚短得到的两端的电压就一定为0.这样就是犯了先入为主的毛病，在很多情况下也是需要将Up与Un的值求出代数再进行下一步运算的。根据“虚短”只能得出Up = Un，这里也比较好分析，ip的电流为0，R'两端电压为0，所以Up = Ui = Un。

        2.IR = IRf = Ui/R，Uo = Un + IRf * Rf = Un + Rf * Ui/R

        3.将2中的Un替换成Ui，得到 Uo = Ui（1 + Rf/R），此时平衡电阻R' = R//Rf

2. 同相积分运算电路

2.1 同相积分运算电路电路图

2.2 同相积分运算电路电路分析

        1.在同相放大电路的基础上，将反馈电阻Rf改成电容C1，在同相输入端配上平衡电容C2，这样就构成了同相积分运算电路，设置C1 = C2 = C，输入端电阻R阻值相等。

        2.根据虚短、虚断得出：Un = Up，iC1 = i1 = -Un/R

        3.对C1进行分析，在前面的反相积分中我们提到，单位时间内通过导体某一横截面的电荷量就是电流。此时流经C1的电压为Un - Uo，所以iC1 = C* d（Un - Uo）/dt = -Un/R（来自上一步的等式），对等式拆分合并得出：C*dUo = C*dUn / dt + Un / R        

        4.对C2进行分析，i2 = iC2 →（Ui - Up）/R = C*dUp / dt，同样拆分合并该等式得出：Ui/R = C*dUp / dt + Up / R

        5.观察发现，第三步与第四步的右边等式由于Up = Un的关系所以是相等的（这也是在第一步中要强调设置的两个电容和电阻值需要相等的原因），所以左边的等式也相等，得出：Ui / R = C*dUo/dt ，合并：dUo / dt = Ui / RC，对两边同时积分得：

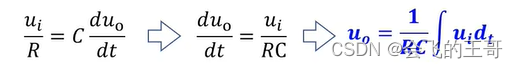
当存在初始电压Uo（to）时，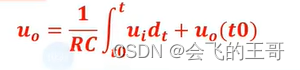

2.3 同相积分与反相积分的区别与联系

        1.在对电路的使用和实际电路仿真中，我们可以看出两种电路都能将方波信号转变为三角波信号以及将正弦信号转变为余弦信号。      

        2.所不同的是在对同一方波信号同时做同相积分和反相积分的处理后，所得的三角波相位相差180度，对正弦信号处理所得的两个余弦信号也是相差180度。