有容量限制的车辆路径规划问题(Capacitated Vehicle Routing Problem)

在看matlab的时候发现了这篇文章https://www.frontiersin.org/articles/10.3389/fict.2019.00013/full

仔细阅读一下。(英语渣渣，自学用)

The Capacitated Vehicle Routing Problem (CVRP) is an NP-optimization problem (NPO) that has been of great interest for decades for both, science and industry. The CVRP is a variant of the vehicle routing problem characterized by capacity constrained vehicles. The aim is to plan tours for vehicles to supply a given number of customers as efficiently as possible. The problem is the combinatorial explosion of possible solutions, which increases superexponentially with the number of customers. Classical solutions provide good approximations to the globally optimal solution.

旨在以尽可能高效的方式为一定数量的客户提供服务。问题在于可能解决方案的组合爆炸，随着客户数量呈超指数级增长。经典解决方案能够提供全局最优解的良好近似。

D-Wave's quantum annealer is a machine designed to solve optimization problems. This machine uses quantum effects to speed up computation time compared to classic computers. The problem on solving the CVRP on the quantum annealer is the particular formulation of the optimization problem.

D-Wave的量子退火器是一台旨在解决优化问题的机器。与经典计算机相比，这台机器利用量子效应加快计算速度。在量子退火器上解决CVRP问题的问题在于优化问题的特定表述。

For this, it has to be mapped onto a quadratic unconstrained binary optimization (QUBO) problem. Complex optimization problems such as the CVRP can be translated to smaller subproblems and thus enable a sequential solution of the partitioned problem. This work presents a quantum-classic hybrid solution method for the CVRP. It clarifies whether the implementation of such a method pays off in comparison to existing classical solution methods regarding computation time and solution quality. Several approaches to solving the CVRP are elaborated, the arising problems are discussed, and the results are evaluated in terms of solution quality and computation time.为此，必须将其映射到二次无约束二进制优化（QUBO）问题上。像CVRP这样的复杂优化问题可以转化为较小的子问题，从而实现分阶段解决问题。这项工作提出了一种用于CVRP的量子-经典混合解决方法。它阐明了这种方法的实施是否值得，相较于现有的经典解决方法，无论是在计算时间还是解决方案质量方面。详细阐述了解决CVRP问题的几种方法，讨论了出现的问题，并根据解决方案质量和计算时间对结果进行评估。

1.Introduction

Optimization problems can be found in many different domains of applications, be it economics and finance (Black and Litterman, 1992), logistics (Caunhye et al., 2012), or healthcare (Cabrera et al., 2011). Their high complexity engaged researchers to develop efficient methods for solving these problems (Papadimitriou and Steiglitz, 1998). With D-Wave Systems releasing the first commercially available quantum annealer in 20111, there is now the possibility to find solutions for such problems in a completely different way than classical computation does. To use D-Wave's quantum annealer the optimization problem has to be formulated as a quadratic unconstrained binary optimization (QUBO) problem (Boros et al., 2007), which is one of two input types acceptable by the machine (alternative: the Ising model Glauber, 1963). Doing this, the metaheuristic quantum annealing seeks for the minimum of the optimization function, i.e., the best solution of the defined configuration space (McGeoch, 2014). There has been recent research about solving real world problems on a quantum annealer, like Volkswagen's Traffic Flow Optimization (Neukart et al., 2017) or the recently announced Tsunami Evacuation Optimization project by Tohoku University.

优化问题可以在许多不同的应用领域中找到，无论是经济和金融（Black and Litterman，1992），物流（Caunhye et al.，2012）还是医疗保健（Cabrera et al.，2011）。它们的高度复杂性促使研究人员开发解决这些问题的有效方法（Papadimitriou和Steiglitz，1998）。2011 年，D-Wave Systems 发布了第一台商用量子退火炉1，现在有可能以与经典计算完全不同的方式找到此类问题的解决方案。为了使用D-Wave的量子退火器，优化问题必须表述为二次无约束二元优化（QUBO）问题（Boros et al.， 2007），这是机器可接受的两种输入类型之一（替代：Ising 模型 Glauber，1963）。这样做，元启发式量子退火寻求优化函数的最小值，即定义的配置空间的最佳解（McGeoch，2014）。最近有关于在量子退火器上解决现实世界问题的研究，如大众汽车的交通流优化（Neukart et al.， 2017）或东北大学最近宣布的海啸疏散优化项目。

The paper at hand regards the Capacitated Vehicle Routing Problem (CVRP), an NP-optimization problem that plays a major role in common operations research and is excessively studied since its proposal in Dantzig and Ramser (1959). The classic CVRP can be described as the problem of designing optimal routes from one depot to a number of geographically scattered customers subject to some side constraints (see Figure 1). It can be formulated as follows:

本文讨论了有能力车辆路径问题（CVRP），这是一个np优化问题，在普通作战研究中起着重要作用，自Dantzig和Ramser（1959）提出以来得到了广泛的研究。经典的CVRP可以被描述为设计从一个仓库到许多地理上分散的客户的最优路线的问题，但会受到一些侧边的约束（见图1）。其可表述如下：

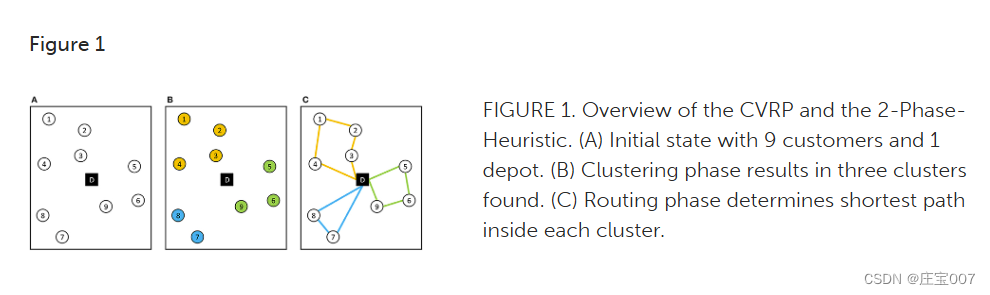​图1所示，CVRP和两阶段启发式的概述:(A)初始状态有9个客户和1个仓库(B)聚类阶段产生3个集群(C)路径由每个集群的最短路径确定。

Let G = (V, E) be a graph with V = {1, …, n} being a set of vertices representing n customer locations with the depot located at vertex 1 and E being a set of undirected edges. With every edge (i, j) ∈ E, i ≠ j a non-negative cost cij is associated. This cost may, for instance, represent the (geographical) distance between two customers i and j. Furthermore, assume there are m vehicles stationed at the depot that have the same capacity Q. In addition, every customer has a certain demand q (Laporte, 1992). The CVRP consists of finding a set of vehicle routes such that

• each customer in V \ {1} is visited exactly once by exactly one vehicle;

• all routes start and end at the depot;

• the sum of customer demand within a route does not exceed the vehicles' capacity;

• the sum of costs of all routes is minimal given the constraints above;

设 G = （V， E） 是一个图，V ={1，…，n}是代表n个客户位置的顶点集合，其中仓库位于顶点1,E是一组无向边。对于每条边 （i， j） ∈ E，i ≠ j 一个非负成本 cij是关联的。例如，此成本可能表示两个客户 i 和 j 之间的（地理）距离。此外，假设有 m 辆车辆驻扎在仓库中，其容量为 Q。此外，每个客户都有一定的需求q（Laporte，1992）。CVRP 包括查找一组车辆路线，以便

• V \ {1} 中的每个客户正好被一辆车访问一次;

• 所有路线的起点和终点都在停车场;

• 路线内的客户需求总和不超过车辆的容量;

• 鉴于上述限制，所有路线的成本总和是最小的;

To solve the CVRP on D-Wave's quantum annealer, the formulated QUBO problem has to be mapped to the hardware. However, quantum computation compared to classical computation is still in its infancy and one of the major problems is that quantum hardware is limited regarding the number of quantum bits (qubits) and their connectivity on the chip. Generally, this leads to difficulties in mapping large QUBO problems to the hardware.为了解决D-Wave量子退火机上的CVRP问题，必须将公式化的QUBO问题映射到硬件上。然而，与经典计算相比，量子计算仍处于起步阶段，其中一个主要问题是量子硬件在量子比特(量子位)数量及其在芯片上的连接方面受到限制。通常，这会导致将大型QUBO问题映射到硬件的困难。

With this paper we present an intuitive way to split the CVRP into smaller optimization problems by taking advantage of a classical 2-Phase-Heuristic (Laporte and Semet, 2002), see Figure 1. This heuristic divides the CVRP into two phases, the clustering phase and the routing phase. The clustering phase itself can be mapped to the NP-complete Knapsack Problem (KP) (Karp, 1972), which tries to pack different sized items (here: customers) into capacity restricted knapsacks (here: vehicles). Doing this, the sum of the objective values of the items in a knapsack should be maximized, i.e., the euclidean distance between customers assigned to a vehicle should be minimized. The routing phase can be represented by the NP-hard Travelling Salesman Problem (TSP) (Biggs, 1986). Thus, the minimal tour in which all customers of a cluster are visited once is sought. Doing this, the tour starts and ends in one place, i.e., the depot.在本文中，我们提出了一种直观的方法，通过利用经典的两阶段启发式(Laporte和Semet, 2002)，将CVRP拆分为更小的优化问题，参见图1。该启发式算法将CVRP划分为两个阶段，即聚类阶段和路由阶段。聚类阶段本身可以映射到np完备的背包问题(KP) (Karp, 1972)，(6 封私信 / 56 条消息) 计算机科学中的「背包问题(Knapsack problem)」是什么，它有什么应用场景？ - 知乎 (zhihu.com)它试图将不同大小的物品(这里是客户)打包到容量有限的背包(这里是车辆)中。这样做，一个背包中物品的客观价值的总和应该是最大的，也就是说，分配给车辆的顾客之间的欧几里得距离应该是最小的。路由阶段可以用NP-hard旅行商问题(TSP)来表示(Biggs, 1986)。因此，寻求一次访问集群中所有客户的最小行程。这样，旅行就在一个地方开始和结束，即仓库。

Figure 1 shows a CVRP example with the 2-Phase-Heuristic. First the customers are grouped into clusters (b) before efficient vehicle routes in each cluster are searched (c).展示了一个带有两阶段启发式的CVRP示例。首先将顾客分组(b)，然后在每个分组中搜索有效的车辆路线(c)。

In this paper we investigate different quantum-classic hybrid approaches to solve the CVRP, expound their difficulties in finding good solutions, and finally propose a hybrid method based on the 2-Phase-Heuristic to solve the CVRP using D-Wave's quantum annealer. We map the optimization problems to a QUBO problem, and analyze performance from an application-specific perspective by using large benchmark datasets.

本文研究了求解CVRP的不同量子经典混合方法，阐述了它们在求解CVRP时存在的困难，最后提出了一种基于两相启发式的混合方法，利用D-Wave的量子退火器求解CVRP。我们将优化问题映射为QUBO问题，并通过使用大型基准数据集从特定于应用程序的角度分析性能。

The paper is structured as follows: section 2 gives an introduction to quantum annealing and the common QUBO problem. A brief overview of existing methods for solving the CVRP is given in section 3. In section 4, two approaches for solving the CVRP are briefly discussed before the concept of our hybrid method is presented. Section 5 first introduces the test setup, and subsequently presents and discusses the results with regard to solution quality and computational performance on commonly used CVRP datasets. Finally, we conclude this paper in section 6.

本文的结构如下:第2节介绍量子退火和常见的QUBO问题。第3节给出了解决CVRP的现有方法的简要概述。在第4节中，在提出混合方法的概念之前，简要讨论了解决CVRP的两种方法。第5节首先介绍了测试设置，随后介绍并讨论了在常用CVRP数据集上关于解决方案质量和计算性能的结果。最后，我们在第六节对本文进行总结。

2. Quantum Annealing on D-Wave Processor

Quantum annealing in general is a metaheuristic for solving complex optimization problems (Kadowaki and Nishimori, 1998). D-Wave's quantum annealing algorithm is implemented in hardware using a framework of analog control devices to manipulate a collection of quantum bit (qubit) states according to a time-dependent Hamiltonian, denoted H(t), shown in Equation (1).

一般来说，量子退火是解决复杂优化问题的元启发式方法(Kadowaki和Nishimori, 1998)。D-Wave的量子退火算法是在硬件中实现的，使用模拟控制设备框架来根据与时间相关的哈密顿量(表示为H(t))来操纵量子比特(qubit)状态的集合，如式(1)所示。

The basic process of quantum annealing is to physically interpolate between an initial Hamiltonian HI with an easy to prepare minimal energy configuration (or ground state), and a problem Hamiltonian HP, whose minimal energy configuration is sought that corresponds to the best solution of the defined problem. This transition is described by an adiabatic evolution path which is mathematically represented as function s(t) and decreases from 1 to 0 (McGeoch, 2014). If this transition is executed sufficiently slow, the probability to find the ground state of the problem Hamiltonian is close to 1 (Albash and Lidar, 2018).

量子退火的基本过程是在具有易于制备的最小能量构型(或基态)的初始哈密顿量HI和寻找与所定义问题的最佳解对应的最小能量构型的问题哈密顿量HP之间进行物理插值。这种转变由绝热演化路径描述，该路径在数学上表示为函数s(t)，从1到0递减(McGeoch, 2014)。如果这种转换执行得足够慢，那么找到问题哈密顿量的基态的概率接近于1 (Albash和Lidar, 2018)。

The just described concept of adiabatic quantum computing is the source of inspiration for the design of D-Wave's quantum annealing hardware. While the machine's functioning is based on following an adiabatic evolution path, the dynamics describing its working is not adiabatic. This is because the machine is strongly coupled to the environment resulting in the performance being affected by dissipative effects (Marshall et al., 2017). Nonetheless, the hardware is known to be capable of solving a specific optimization problem called a quadratic unconstrained binary optimization (QUBO) problem (Boros et al., 2007). QUBO is a unifying model which can be used for representing a wide range of combinatorial optimization problems. However, in order to use quantum annealing on D-Wave's hardware the CVRP has to be formulated as a QUBO problem. The functional form of the QUBO the quantum annealer is designed to minimize is:

刚才描述的绝热量子计算概念是D-Wave量子退火硬件设计的灵感来源。虽然机器的功能是基于遵循绝热演化路径，但描述其工作的动力学不是绝热的。这是因为机器与环境强耦合，导致性能受到耗散效应的影响(Marshall等人，2017)。尽管如此，已知硬件能够解决称为二次无约束二进制优化(QUBO)问题的特定优化问题(Boros等人，2007)。QUBO是一种统一的模型，可用于表示广泛的组合优化问题。然而，为了在D-Wave的硬件上使用量子退火，CVRP必须被表述为QUBO问题。量子退火炉设计的QUBO的功能形式最小化为:

with x being a vector of binary variables of size n, and Q being an n × n real-valued matrix describing the relationship between the variables. Given the matrix Q, the annealing process tries to find binary variable assignments to minimize the objective function in Equation (2).

其中x是大小为n的二元变量的向量，Q是描述变量之间关系的n × n实值矩阵。给定矩阵Q，退火过程试图找到二值变量赋值以最小化式(2)中的目标函数。

The quantum processing unit (QPU) is a physical implementation of an undirected graph with qubits as vertices and couplers as edges between them. These qubits are arranged according in a so-called chimera graph, as illustrated in Figure 2. In relation to the QUBO problem, each qubit on the QPU represents such a QUBO variable and couplers between qubits represent the costs associated with qubit pairs, mathematically described in matrix Q. If the problem structure can not be embedded directly to the chimera graph, auxiliary qubits may be introduced to augment the available couplings.

量子处理单元(QPU)是一个无向图的物理实现，量子比特作为顶点，耦合器作为它们之间的边。这些量子位按照所谓的嵌合体图排列，如图2所示。对于QUBO问题，QPU上的每个量子位代表这样一个QUBO变量，量子位之间的耦合器代表与量子位对相关的成本，在数学上用矩阵q描述。如果问题结构不能直接嵌入到嵌合体图中，可以引入辅助量子位来增加可用的耦合。

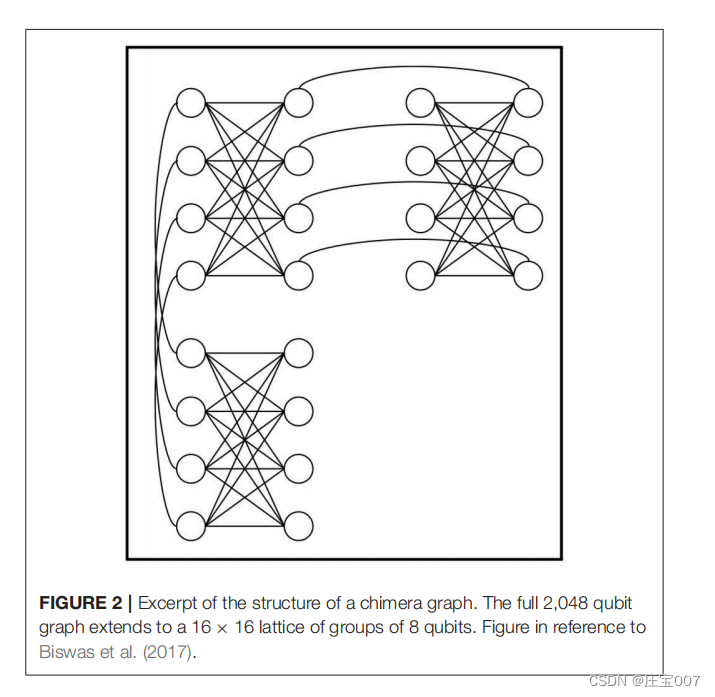
一个嵌合拉图的结构摘录。完整的2048量子位图扩展到一个8个量子位群的16×16格。图参考Biswas等人。

If—like in this paper—large data sets are used, the size of the resulting QUBO problem may exceed the limited number of available qubits on the QPU and the problem cannot be put on the chip altogether anymore. For this case, D-Wave provides a tool called QBSolv that splits the QUBO into smaller components and solves them sequentially on the D-Wave hardware3. A detailed view on the QBSolv algorithm is given in section 5.1.

如果像本文中那样使用大型数据集，那么由此产生的QUBO问题的大小可能会超过QPU上可用量子位的有限数量，并且问题无法完全放在芯片上。对于这种情况，D-Wave提供了一个名为QBSolv的工具，它将QUBO拆分为更小的组件，并在D-Wave硬件上依次解决它们。第5.1节给出了QBSolv算法的详细视图。

In this paper we used the D-Wave 2000Q model located in Vancouver, Canada, and we accessed the machine using D-Wave's cloud interface. The instance at hand has got a working graph with 2,038 qubits and 5,955 couplers out of the full graph with 2,048 qubits and 6,016 couplers.在本文中，我们使用位于加拿大温哥华的D-Wave 2000Q模型，我们使用D-Wave的云接口访问机器。当前实例的工作图包含2,038个量子位和5,955个耦合器，而完整图包含2,048个量子位和6,016个耦合器。

3. Related Work

Over the last decades several families of heuristics have been proposed for solving the CVRP. They can be divided into construction heuristics, improvement heuristics and metaheuristics (Laporte and Semet, 2002).

在过去的几十年里，人们提出了几种启发式方法来解决CVRP问题。它们可以分为构建启发式、改进启发式和元启发式(Laporte和Semet, 2002)。

Construction heuristics try to generate a good solution gradually. In every step, they insert customers into partial tours or combine sub-tours considering some capacities and costs to generate a complete solution. One of the most fundamental construction heuristics is the Clarke and Wright savings algorithm (Clarke and Wright, 1964), which first constructs a single tour for each customer, calculates the saving that can be obtained by merging those single customer tours, and iteratively combines the best sub-tours until no saving can be obtained anymore.

构建启发式试图逐步产生一个好的解决方案。在每一步中，他们将客户插入到部分行程中，或者结合考虑一些容量和成本的子行程，以生成完整的解决方案。最基本的构造启发式方法之一是Clarke and Wright节省算法(Clarke and Wright, 1964)，该算法首先为每个客户构建一个单独的行程，计算合并这些单个客户行程所能获得的节省，并迭代地组合最佳子行程，直到无法再获得节省。

Improvement heuristics try to iteratively enhance a given feasible solution, which is often generated by a construction heuristic. A common methodology is to replace or swap customers between sub-tours taking capacity constraints into account. Popular improvement methods can be found in Lin (1965) and Or (1976). 

改进启发式尝试迭代地增强给定的可行解决方案，这通常是由构造启发式产生的。一种常见的方法是在考虑容量限制的情况下在子旅行之间替换或交换客户。流行的改进方法可以在Lin(1965)和Or(1976)中找到。

Metaheuristics can be thought of as top-level strategies which guide local improvement operators to find a global solution. Groër et al. describe a library of local search heuristics for the (C)VRP (Groër et al., 2010). In addition, Crispin and Syrichas propose a classical quantum annealing metaheuristic for vehicle scheduling (Crispin and Syrichas, 2013). To approximate quantum annealing on a classical computer, they use a stochastic variant called Path-Integral Monte Carlo (PIMC) to simulate the quantum fluctuations of a quantum system. In our work, the quantum annealing hardware is responsible for that. However, the complexity exists in mapping the CVRP to a format readable by the hardware.

元启发式可以被认为是指导局部改进操作者找到全局解决方案的顶层策略。Groër等人描述了(C)VRP的本地搜索启发式库(Groër等人，2010)。此外，Crispin和Syrichas提出了一种经典的量子退火元启发式车辆调度方法(Crispin和Syrichas, 2013)。为了在经典计算机上近似量子退火，他们使用一种称为路径积分蒙特卡罗(PIMC)的随机变体来模拟量子系统的量子波动。在我们的工作中，量子退火硬件负责这一点。但是，将CVRP映射为硬件可读的格式存在复杂性。

One of the most important classical 2-Phase-Heuristics is the Sweep algorithm (Gillett and Miller, 1974), where feasible clusters are formed by rotating a ray centered at the depot. After that the TSP is solved for each cluster. Fisher and Jaikumar also tried to solve the VRP with a cluster-first, route-second algorithm (Fisher and Jaikumar, 1981). They formulated a Generalized Assignment Problem (GAP) instead of using a geometry based method to form the clusters. Bramel and Simchi-Levi described a 2-Phase-Heuristic where the seeds were determined by solving capacitated location problems and the remaining vertices were gradually included into their allotted route in a second stage (Bramel and Simchi-Levi, 1995).最重要的经典两阶段启发式算法之一是扫描算法(Gillett和Miller, 1974)，其中可行的集群是通过旋转以仓库为中心的射线形成的。然后求解每个集群的TSP。Fisher和Jaikumar也尝试用集群优先，路由第二的算法来解决VRP (Fisher和Jaikumar, 1981)。他们提出了一个广义分配问题(GAP)，而不是使用基于几何的方法来形成聚类。Bramel和Simchi-Levi描述了一种两阶段启发式算法，其中通过求解有能力定位问题来确定种子，剩余的顶点在第二阶段逐渐被纳入分配的路线(Bramel和Simchi-Levi, 1995)。

However, there are similar investigations performed by the quantum computing community. In Rieffel et al. (2015), the authors have studied the effectiveness of a quantum annealer in solving small instances within families of hard operational planning problems under various mappings to QUBO problems and embeddings. While their study did not produce results competitive with state-of-the-art classical approaches, they derive insights from the results, useful for the programming and design of future quantum annealers. In our work we investigate larger routing problem instances using a classical quantum hybrid method and state the effectiveness and efficiency. 然而，量子计算社区也进行了类似的调查。在Rieffel et al.(2015)中，作者研究了量子退火器在各种映射到QUBO问题和嵌入的情况下解决硬操作计划问题族中的小实例的有效性。虽然他们的研究没有产生与最先进的经典方法竞争的结果，但他们从结果中获得了见解，对未来量子退火炉的编程和设计有用。在我们的工作中，我们使用经典的量子混合方法研究了较大的路由问题实例，并说明了该方法的有效性和效率。

In Tran et al. (2016), a tree-search based quantum-classical framework is presented. The authors use a quantum annealer to sample from the configuration space of a relaxed problem to obtain strong candidate solutions and then apply a classical processor that maintains a global search tree. They empirically test their algorithm and compare the variants on small problem instances from three scheduling domains. In general, one can see that many approaches have got a hybrid structure. That is, classical bottlenecks are outsourced to quantum computing devices that iteratively perform local quantum searches (Haddar et al., 2016; Tran et al., 2016; Chancellor, 2017).Tran等人(2016)提出了一种基于树搜索的量子经典框架。利用量子退火器从松弛问题的组态空间中进行采样，得到强候选解，然后应用经典处理器维护全局搜索树。他们对算法进行了实证测试，并在三个调度领域的小问题实例上比较了算法的变体。一般来说，我们可以看到很多方法都有混合结构。也就是说，经典瓶颈被外包给迭代执行局部量子搜索的量子计算设备(Haddar等人，2016;Tran et al.， 2016;总理,2017)。

4. Concept of Hybrid Solution Method

There are numerous heuristics in the literature for solving the CVRP that all have an iterative approach. This makes it difficult to map them into a QUBO problem to be solved on a quantum annealer. In addition, there exists the classical 2-Phase-Heuristic that separates the CVRP into a clustering phase and a routing phase. Both phases can be seen as detached optimization problems, the Knapsack Problem (KP) with an additional minimization of distances between customers and the Travelling Salesman Problem (TSP), respectively. This division allows the mapping of the problems to one or two QUBO matrices.

文献中有许多用于求解 CVRP 的启发式方法，它们都具有迭代方法。这使得很难将它们映射到要在量子退火器上求解的 QUBO 问题。此外，还存在经典的 2 阶段启发式方法，将 CVRP 分为聚类阶段和路由阶段。这两个阶段都可以看作是分离的优化问题，分别是背包问题（KP）和旅行推销员问题（TSP），前者是客户之间距离的最小化。这种划分允许将问题映射到一个或两个 QUBO 矩阵。

 We have investigated three different approaches for the 2-Phase-Heuristic using a quantum annealer, see Figure 3. The insights of the preliminary exploration will be given in section 4.1. The concept of the most suitable approach—called Hybrid Solution (HS)—will be presented in detail in sections 4.2 and 4.3.

我们研究了使用量子退火器进行 2 相启发式的三种不同方法，见图 3。初步探索的见解将在第4.1节中给出。最合适的方法的概念（称为混合解决方案 （HS））将在 4.2 和 4.3 节中详细介绍。

 4.1Preliminary Exploration

第一种基于两相启发式的方法将CVRP划分为两个独立的优化问题（图3中的Q2Q）。聚类阶段可以看作是背包问题，在要分组的客户之间有额外的距离最小化。路由阶段可以简化为熟悉的旅行推销员问题。因此，可以将 CVRP 拆分为两个单独的 QUBO 问题并按顺序执行它们。路由阶段的 QUBO 公式与 Lucas （2014） 中提出的 TSP 表示完全对应。然而，聚类阶段的 QUBO 公式是对 Lucas （2014） 所述的背包问题的改编。它由 H = HA + HB + HC 组成，其中 

As the CVRP usually needs to fill several routes m (i.e., backpacks) with customers, the original formulation of Lucas (2014), which takes only one backpack into account, has been adapted accordingly with HA (Equation 3). The first term of HA ensures that the backpack has only one capacity constraint. That is, as soon as two or more yn variables are set to 1, a penalty value X (very high value) is added to the solution what declares it as bad or invalid. The second term, in turn, ensures that the sum of packed objects does not exceed the specified backpack capacity from the first term.

由于CVRP通常需要用客户填充几条路线（即背包），因此Lucas（2014）的原始公式仅考虑一个背包，已相应地调整为HA（公式3）。HA 的第一个术语确保背包只有一个容量限制。也就是说，一旦将两个或多个 yn 变量设置为 1，就会向解决方案中添加一个惩罚值 X（非常高的值），该值声明它为错误或无效。反过来，第二项确保包装物品的总和不超过第一项规定的背包容量。

As soon as the difference is not equal to 0, the squaring and the penalty value A also classify the solution as bad. HB (Equation 4) guarantees that every object or customer must be packed in just one backpack or route. Finally, HC (Equation 5) is an additional optimization function that tries to improve the clustering by grouping the customers that are close to each other. To do this, the distances between the customers of a cluster are summed up.

一旦差值不等于 0，平方和惩罚值 A 也会将解归类为坏解。HB（公式 4）保证每个物品或客户都必须装在一个背包或路线中。最后，HC（公式 5）是一个额外的优化函数，它试图通过对彼此接近的客户进行分组来改进聚类。为此，需要将集群的客户之间的距离相加。

Duv corresponds to the Euclidean distance between customers u and v. The solution with the shortest summed distances within the clusters is the optimum of a classical clustering. The penalty value X must be greater than A and A greater than C. This ensures that in fact only one capacity limit per vehicle is set and each customer is assigned to exactly one vehicle. Experimental tests for different CVRP datasets and problem sizes yielded the following correlation of the penalty values: X = A2 and A = max(Duv) * number of customers. C corresponds to an edge weighting of the clustering, which is used to optimize the clustering.

Duv 相当于客户 u 和 v 之间的欧氏距离。簇内距离总和最短的解就是经典聚类的最优解。惩罚值 X 必须大于 A，而 A 又必须大于 C。这就确保了事实上每辆车只设置了一个容量限制，并且每个客户都被精确分配到一辆车上。针对不同的 CVRP 数据集和问题规模进行的实验测试得出了以下惩罚值的相关性： X = A^2 和 A = max(Duv) * 客户数量。C 相当于聚类的边缘权重，用于优化聚类。第二种方法试图同时而不是按顺序解决每个 CVRP 子问题（图 3 中的 Q1Q）。为此，必须将这些子问题映射为一个单一的 QUBO 问题。这个 QUBO 问题的整体解决方案如下：

 HA corresponds to Equation (3) of the first approach. The first term also ensures that the m vehicles have a clear capacity constraint while the second term ensures that the vehicle capacity determined by the first term is not exceeded by the summed customer demand.

HA 相当于第一种方法的公式 (3)。第一项还确保 m 辆车有明确的容量限制，而第二项则确保第一项确定的车辆容量不超过客户需求总和。

HB′ (等式 6）与第一种方法的等式 4 相似。不过，这里还需要考虑路线中的位置，因为在这种方法中，集群和集群内的路线都是同时解决的。

Thus, this term means that a customer can only be assigned exactly one route with exactly one position within this route. HC corresponds to Equation (5) of the first approach and is responsible for optimizing the clustering. That is, we try to assign customers who have a small distance from each other to a route. HD (Equation 7) ensures that each position j can only be assigned to exactly one customer α and one route k. Finally, the shortest route within a cluster must be found. This is optimized with HE (Equation 8). Since each position is unique across all routes, the route subdivision can be neglected here. It should also be noted that in the Q1Q approach the depot needs to be mapped to each cluster in order to properly execute the TSP in each cluster. HF causes the depots that were inserted multiple times in the dataset to be assigned to different clusters each, where d corresponds to the number of depots or the number of vehicles.

因此，这个术语意味着一个客户只能被分配到一条路线，而在这条路线中只能有一个位置。HC 与第一种方法的公式 (5) 相对应，负责优化聚类。也就是说，我们尽量将彼此距离较小的客户分配到一条线路上。HD（等式 7）确保每个位置 j 只能分配给一个客户 α 和一条线路 k。这可以通过 HE 进行优化（公式 8）。由于每个位置在所有路线中都是唯一的，因此可以忽略路线细分。还应注意的是，在 Q1Q 方法中，为了在每个集群中正确执行 TSP，需要将车厂映射到每个集群。高频会导致在数据集中多次插入的车厂分别被分配到不同的集群，其中 d 相当于车厂数量或车辆数量。

However, in the second approach we observed that both optimization functions (HC and HE) seemed to hinder each other. Neglecting the clustering optimization function (HC) led to valid routes inside the clusters, but at the same time the clusters were very sparse. The other way round, i.e., neglecting the routing optimization function HE, led to dense clusters but also to invalid routes inside the clusters. In summary, both efforts lead to invalid or unusable solutions.

然而，在第二种方法中，我们发现两个优化功能（HC 和 HE）似乎相互阻碍。忽略集群优化功能（HC）会导致集群内的路线有效，但同时集群非常稀疏。反之，即忽略路由优化函数 HE，则会导致集群密集，但同时集群内的路由也无效。总之，这两种方法都会导致无效或无法使用的解决方案。

The third approach (HS in Figure 3) as a candidate for a CVRP solution method combines the positive aspects of the previous mentioned approaches. To achieve this, the clustering phase (KP) is solved using a classical algorithm while the routing phase (TSP) is mapped to a QUBO problem in order to solve it on the quantum annealer. The following Subsections will go into detail.作为 CVRP 解决方案候选方法的第三种方法（图 3 中的 HS）结合了前几种方法的优点。为此，聚类阶段（KP）采用经典算法求解，而路由阶段（TSP）则映射为 QUBO 问题，以便在量子退火器上求解。以下分节将详细介绍。

4.2 Hybrid Solution—Clustering Phase(混合解决方案-聚类阶段)

The clustering phase of the hybrid solution method we propose is inspired by Shin and Han (2011). Based on their work, we add a characteristics called clustering core point parameter that will be presented below. The clustering phase can be subdivided: (1) cluster generation and (2) cluster improvement.

我们提出的混合求解方法的聚类阶段受到了 Shin 和 Han（2011 年）的启发。在他们工作的基础上，我们添加了一个称为聚类核心点参数的特征，将在下文中介绍。聚类阶段可细分为：（1）聚类生成和（2）聚类改进。

Within the cluster generation the core stop of a cluster, i.e., the first customer in a cluster, is chosen. Koenig (1995) propose to select the core stop either based on the maximum demand of the customers, or based on the largest distance to the depot. The motivation behind choosing the customer with the highest demand is the assumption that this one is the most critical customer in relation to the vehicles' capacity constraint. After selecting that particular customer, the vehicle can be filled with goods for customers having a smaller demand.

在集群生成过程中，选择集群的核心站点，即集群中的第一个客户。Koenig （1995）建议根据客户的最大需求量或与仓库的最大距离来选择核心站。之所以选择需求量最大的客户，是因为假定该客户是与车辆运力限制相关的最关键客户。选择该客户后，车辆可为需求量较小的客户装满货物。

The motivation behind choosing the customer with the largest distance to the depot is the assumption that this one is the most critical customer in relation to the routes' length constraint and that other customers may be supplied while approaching or receding that particular customer. Once the core stop v of a cluster has been selected, the geometric center CC(mk) of cluster mk is calculated using

之所以选择与车厂距离最大的客户，是因为假设该客户是与路线长度限制相关的最重要客户，而且在接近或离开该客户时，可能会向其他客户提供服务。一旦选定了集群的核心站点 v，集群 mk 的几何中心 CC(mk) 的计算公式为

 

the customer with the smallest distance to the cluster center is selected from the set of unclustered customers and added to the cluster. After the cluster center is recalculated the steps are repeated until the demand of a customer to be added would exceed the vehicle's capacity. If this is the case, a new core stop is selected based on the previously explained criteria and the still unclustered customers are assigned to the new cluster. This procedure stops when each customer has been assigned to a cluster.

从未分类的客户集合中选出与集群中心距离最小的客户，并将其添加到集群中。重新计算集群中心后，重复上述步骤，直到要添加的客户需求超过车辆的容量。如果出现这种情况，就会根据之前说明的标准选择一个新的核心站，并将仍未聚类的客户分配到新的聚类中。当每个客户都被分配到一个群组后，该程序就会停止。

Once the clusters have been generated, the cluster improvement is executed to enhance the clusters. This step assigns a customer vi belonging to cluster mk to another cluster mj, if that would reduce the distance to the cluster center, i.e., if the distance to CC(mj) is smaller than the distance to CC(mk). However, assigning a customer to a new cluster must not violate the capacity limitation. If the reassignment is possible and valid, CC(mj) and CC(mk) are recalculated and the improvement process begins again. The improvement step terminates if it is not possible to assign a customer to another cluster or when a certain stop criterion is reached (e.g., number of iterations).

聚类生成后，将执行聚类改进以增强聚类。这一步会将属于簇 mk 的客户 vi 分配到另一个簇 mj，前提是这样能减少与簇中心的距离，即与 CC(mj) 的距离小于与 CC(mk) 的距离。但是，将客户分配到新的群组不得违反容量限制。如果重新分配可行且有效，则重新计算 CC(mj) 和 CC(mk)，并重新开始改进过程。如果无法将客户分配到另一个群组，或达到某个停止标准（如迭代次数），则改进步骤终止。

4.3 Hybrid Solution—Routing Phase(混合解决方案--路由阶段)

After the clustering phase is completed, the goal is now to find the shortest route inside each cluster. Thus, the Travelling Salesman Problem (TSP) is executed for every generated cluster. The TSP can be reduced to the Hamiltonian Cycle Problem (HPC), which can be formulated as QUBO problem as follows (Lucas, 2014):

聚类阶段完成后，现在的目标是找到每个聚类内部的最短路径。因此，每个生成的集群都要执行旅行推销员问题（TSP）。TSP 可以简化为汉密尔顿循环问题（Hamiltonian Cycle Problem，HPC），可表述为如下 QUBO 问题（Lucas，2014）：

The binary variable xi, j is 1 if the customer with index i is located at position j in the Hamiltonian Cycle. The first term (constraint) requires that each customer must occur only once in the cycle, while the second term enforces that each position in the cycle must be assigned to exactly one customer. This defines the order of the customers within the tour. The squared differences of these terms ensure that exactly one customer has a unique position in the tour. Otherwise, a high penalty value A would be added to the solution energy, which states the solution itself as suboptimal or rather invalid. 

如果索引为 i 的客户位于汉密尔顿循环中的位置 j，则二进制变量 xi, j 为 1。第一项（约束条件）要求每位顾客在循环中只能出现一次，而第二项则强制要求循环中的每个位置必须分配给一位顾客。这就定义了客户在巡回中的顺序。这些项的平方差确保了恰好有一位顾客在巡回中拥有唯一的位置。否则，解的能量中就会增加一个高惩罚值 A，从而说明解本身是次优的，或者说是无效的。

 Although different penalties are possible for the two terms, we choose the same value because we consider both constraints equally important. The third term ensures that the order of customers found is possible. That is, if xu, j and xi, j+1 are both 1 and (ui) ∉ E with E being the set of edges between the nodes representing the customers, then the penalty value A should also state the solution invalid (Lucas, 2014). In this work we have evaluated our algorithm using CVRP/TSP datasets with fully meshed vertices, i.e., customers are connected with undirected edges. That is why the third term can be neglected.虽然这两个项可能有不同的惩罚，但我们选择了相同的值，因为我们认为这两个约束条件同样重要。第三项确保找到的客户顺序是可能的。也就是说，如果 xu, j 和 xi, j+1 均为 1 且 (ui) ∉ E（E 是代表客户的节点之间的边集），那么惩罚值 A 也应说明解决方案无效（Lucas，2014 年）。在这项工作中，我们使用全网格顶点的 CVRP/TSP 数据集对算法进行了评估，即客户是通过无向边连接的。因此第三项可以忽略。

为了找到长度最短的哈密顿周期，需要使用以下最小化函数：

Here Dui is the euclidean distance between the customers u and i. The minimization function sums all costs of the edges between successive customers. The total solution for the TSP QUBO problem is then composed of:Dui 是客户 u 和 i 之间的欧氏距离。最小化函数将连续客户之间边的所有成本相加。因此，TSP QUBO 问题的总解由以下部分组成：

The penalty value B must be chosen sufficiently small so that it does not violate the constraint HA. A possible choice would be 0 < B · max(Dui) < A (Lucas, 2014). With B = 1, A has to be chosen larger than the greatest distance between two customers. In our experiments B was set to 1 and A was set to n · max(Dui) with n being the number of customers.

惩罚值 B 必须选得足够小，这样才不会违反 HA 约束。可能的选择是 0 < B - max(Dui) < A（卢卡斯，2014 年）。当 B = 1 时，A 必须大于两个客户之间的最大距离。在我们的实验中，B 被设为 1，A 被设为 n - max(Dui)，n 为客户数。

By multiplying the QUBO formulas, one obtains the coefficients for the QUBO problem matrix which can be written as a lower (or upper) triangular matrix to be mapped to the quantum annealing processor. Figure 4 shows an excerpt of an exemplary QUBO problem in which only the coefficients are entered for simplification. As soon as several coefficients are noted on one cell of the matrix they must be added. In addition, every coefficient is multiplied with the penalty value A and the distance is multiplied with penalty value B.

通过与 QUBO 公式相乘，可以得到 QUBO 问题矩阵的系数，该矩阵可以写成下（或上）三角矩阵，并映射到量子退火处理器中。图 4 显示了一个示例 QUBO 问题的摘录，其中只输入了系数以简化问题。一旦矩阵的一个单元格中出现多个系数，就必须将其相加。此外，每个系数都要乘以惩罚值 A，距离则乘以惩罚值 B。

 5. Evaluation

In this section we present the results of the hybrid solving method with regards to solution quality and computational results. First the preliminaries for the test setup are given, then the test results are shown.在本节中，我们将介绍混合求解方法在求解质量和计算结果方面的成果。首先介绍测试设置的初步情况，然后展示测试结果。

5.1Preliminaries

As already mentioned, the D-Wave quantum annealer can be regarded as a discrete optimization machine that accepts problems in QUBO formulation. The QUBO problem matrix increases with the problem size, i.e., with the number of problem variables used. For the TSP n2 logical variables, with n being the number of customers, have to be used to describe it as a QUBO problem (see section 4.3). These variables have to be mapped to the qubits and the logical links between them to the couplers of the physical QPU. Because of the almost fully meshed dependencies between the logical variables it is not possible that the logical problem structure matches the physical one. For such issues D-Wave provides a minor embedding technique to find a valid embedding to the hardware, as described in Cai et al. (2014). We have used this technique4 in combination with D-Wave's QBSolv tool to fit our large QUBO problems to the physical hardware.
如前所述，D-Wave 量子退火器可被视为一种离散优化机器，可接受 QUBO 格式的问题。QUBO 问题矩阵随着问题规模（即使用的问题变量数量）的增加而增加。就 TSP 而言，必须使用 n2 个逻辑变量（n 表示客户数量）才能将其描述为 QUBO 问题（见第 4.3 节）。这些变量必须映射到量子比特，而量子比特之间的逻辑链路必须映射到物理 QPU 的耦合器。由于逻辑变量之间存在几乎完全网状的依赖关系，因此逻辑问题结构不可能与物理问题结构相匹配。针对此类问题，D-Wave 提供了一种次要嵌入技术，以找到对硬件的有效嵌入，如 Cai 等人（2014 年）所述。我们将该技术4 与 D-Wave 的 QBSolv 工具结合使用，将大型 QUBO 问题与物理硬件相匹配。
QBSolv splits the QUBO into smaller components (subQUBOs) of a predefined subproblem size5, which are then solved independently of each other. This process is executed iteratively as long as there is an improvement and it can be defined using the QBSolv parameter num_repeats. This parameter determines the number of times to repeat the splitting of the QUBO problem matrix after finding a better sample. With doing so, the QUBO matrix is split into different components using a classical tabu search heuristic in each iteration. QBSolv can be used in a completely classical way to solve the subQUBOs or as a quantum-classic hybrid method by solving the single subQUBOs on the quantum annealer.

QBSolv 将 QUBO 分解成预定义子问题大小5 的较小部分（子 QUBO），然后独立求解。只要有改进，这个过程就会反复执行，可以使用 QBSolv 参数 num_repeats 来定义。该参数决定了在找到更好的样本后，重复分割 QUBO 问题矩阵的次数。这样，QUBO 矩阵就会在每次迭代中使用经典的塔布搜索启发式分割成不同的部分。QBSolv 可用于以完全经典的方式求解子 QUBO，也可作为量子经典混合方法，在量子退火器上求解单个子 QUBO。

Besides embedding and splitting the QUBO into subQUBOs, QBSolv also takes care of the unembedding and the merging of the subproblems' solutions. We use the default configuration of D-Wave's QBSolv6 including the auto_scale function that automatically scales the values of the QUBO matrix to the allowed range of values for the biases and strengths of qubits and couplers. The single-shot annealing time is set to the default value of 20μs. For more details about QBSolv, see Michael Booth and Roy (2017).除了将 QUBO 嵌入和拆分成子 QUBO 之外，QBSolv 还负责解嵌入和合并子问题的解。我们使用 D-Wave QBSolv6 的默认配置，包括自动缩放功能（auto_scale），该功能可自动将 QUBO 矩阵的值缩放至量子比特和耦合器偏置和强度的允许值范围。单次退火时间设置为默认值 20μs。有关 QBSolv 的更多详情，请参见 Michael Booth and Roy (2017)。

There exist many different benchmark datasets for the CVRP and the TSP, which can be downloaded from Xavier (2014), Reinelt (2013), and Cook (2009). In addition, the Best Known Solution (BKS) of each dataset is noted. It gives information about the best solution, i.e., the shortest euclidean distance found by any solution method. In order to test and compare the proposed hybrid solution method with regard to the solution quality, various test datasets of Christofides and Eilon (Xavier, 2014) have been selected. Details about the CVRP datasets can be extracted from the name with the format E-nX-kY. For example, E-n22-k4 stands for a certain dataset E, n22 for the number of customers including the depot and k4 for the minimal number of vehicles needed to solve the problem. The TSP datasets have the name format CityX, which just indicates the number of customers which have to be visited in the TSP tour. As already mentioned, the customer and depot coordinates relate to a 2D euclidean space.

CVRP 和 TSP 有许多不同的基准数据集，可从 Xavier（2014 年）、Reinelt（2013 年）和 Cook（2009 年）下载。此外，每个数据集的最佳已知解（BKS）都有记录。它提供了最佳解决方案的信息，即任何解决方案找到的最短欧氏距离。为了测试和比较所提出的混合求解方法的求解质量，我们选择了克里斯托菲德斯和埃隆（Xavier，2014 年）的各种测试数据集。有关 CVRP 数据集的详细信息可从名称中提取，格式为 E-nX-kY。例如，E-n22-k4 代表某个数据集 E，n22 代表包括仓库在内的客户数量，k4 代表解决问题所需的最小车辆数量。TSP 数据集的名称格式为 CityX，表示在 TSP 行程中必须访问的客户数量。如前所述，客户和车厂坐标与二维欧几里得空间有关。

（累了，过几天再编辑）