数据操作
三维:图片(宽,高,通道) 四维:一批图片(批量大小,宽,高,通道) 五维:视频(批量大小,时间,宽,高,通道)
访问元素:一个[1,2] 一行[1,:] 一列[:,1] 子区域[1:3,1:] 子区域[::3,::2](行每三行一跳,列每两列一跳)
访问形状:x.shape 元素总数x.numpy 改变形状x.reshape(3,4)
创建数组:torch.tensor([[1,2,3],[1,2,3]]) torch.zeros((2,3,4)) torch.ones((2,3,4))
数组连结:torch.cat((X,Y),dim = 0)按行合并 , dim=1按列合并
内存问题:
before = id(Y)
Y = Y+X
id(Y) = before #False
before = id(Y)
Y += X # Z = torch,zeros_like(Y) Z[:]=X+Y
id(Y) = before #True
数据预处理
- 读取数据集
import os
#创建目录
os.makedirs(os.path.join('..', 'data'), exist_ok=True)#exist_ok=True表示如果目录已经存在,则不会引发异常。
data_file = os.path.join('..', 'data', 'house_tiny.csv')’#这里以house_tiny为例
with open(data_file, 'w') as f:
f.write('NumRooms,Alley,Price\n') # 列名
f.write('NA,Pave,127500\n') # 每行表示一个数据样本
f.write('2,NA,106000\n')
f.write('4,NA,178100\n')
f.write('NA,NA,140000\n')
import pandas as pd
data = pd.read_csv(data_file)
print(data)
# NumRooms Alley Price
#0 NaN Pave 127500
#1 2.0 NaN 106000
#2 4.0 NaN 178100
#3 NaN NaN 140000
-
处理缺失值
-
插值法(这里采用的)
-
删除法(直接忽略缺失值)
-
# 这里用iloc将data分为inputs(前两列),outputs(后一列)
inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2]
inputs = inputs.fillna(inputs.mean())# 用同一列的均值替换NAN值
print(inputs)
# NumRooms Alley
#0 3.0 Pave
#1 2.0 NaN
#2 4.0 NaN
#3 3.0 NaN 只处理了数字列
?类别列怎么处理
inputs = pd.get_dummies(inputs, dummy_na=True)#pd.get_dummies()用于将分类变量转换为虚拟变量,并且在原始数据中用1表该取值存在,0表该取值不存在
print(inputs)
# NumRooms Alley_Pave Alley_nan
#0 3.0 1 0
#1 2.0 0 1
#2 4.0 0 1
#3 3.0 0 1
转换为张量
import torch
X = torch.tensor(inputs.to_numpy(dtype=float))
y = torch.tensor(outputs.to_numpy(dtype=float))
X, y
'''(tensor([[3., 1., 0.],
[2., 0., 1.],
[4., 0., 1.],
[3., 0., 1.]], dtype=torch.float64),
tensor([127500., 106000., 178100., 140000.], dtype=torch.float64))'''
线性代数
降维:
# 求和
A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape #(array([40., 45., 50., 55.]), (4,))
A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape #(array([ 6., 22., 38., 54., 70.]), (5,))
A.sum(axis=[0, 1]) # array(190.),结果和A.sum()相同
# 求平均
A.mean(), A.sum()/A.size # (array(9.5), array(9.5))
A.mean(axis=0), A.sum(axis=0)/A.shape[0] #(array([ 8., 9., 10., 11.]), array([ 8., 9., 10., 11.]))
非降维求和
sum_A = A.sum(axis=1, keepdims=True)
sum_A
'''>>> sum_A =A.sum(axis=1)
tensor([3, 7])
>>> sum_A = A.sum(axis=1,keepdims=True)
tensor([[3],
[7]])'''
累积求和
>>> A
tensor([[1, 2],
[3, 4]])
>>> A.cumsum(axis=0)
tensor([[1, 2],
[4, 6]])
点积
向量之间按元素乘积的和
矩阵-向量积
A.shape, x.shape, np.dot(A, x)
#((5, 4), (4,), array([ 14., 38., 62., 86., 110.]))
矩阵-矩阵乘法
B = np.ones(shape=(4, 3))
np.dot(A, B)
'''array([[ 6., 6., 6.],
[22., 22., 22.],
[38., 38., 38.],
[54., 54., 54.],
[70., 70., 70.]])'''
范数
向量的范数是表示一个向量有多大
L 2 L_2 L2范数的计算
u = np.array([3, -4])
np.linalg.norm(u)
#array(5.)
L 1 L_1 L1范数的计算
np.abs(u).sum()
#array(7.)
计算矩阵的Frobenius范数
np.linalg.norm(np.ones((4, 9)))
# array(6.)
自动微分
简单例子介绍一下求梯度
import torch
x = torch.arange(4.0)
x #tensor([0., 1., 2., 3.])
x.requires_grad_(True) # 等价于x=torch.arange(4.0,requires_grad=True)
x.grad # 默认值是None
y = 2 * torch.dot(x, x)
y
y.backward()
x.grad # tensor([ 0., 4., 8., 12.])
# 在默认情况下,PyTorch会累积梯度,我们需要清除之前的值
x.grad.zero_()
y = x.sum()
y.backward()
x.grad
非标量变量的反向传播
当y不是标量时,向量y关于向量x的导数的最自然解释是一个矩阵。 对于高阶和高维的y和x,求导的结果可以是一个高阶张量。
# 对非标量调用backward需要传入一个grad参数,该参数指定微分函数关于self的梯度。
# 本例只想求偏导数的和,所以传递一个1的梯度是合适的
x.grad.zero_()
y = x * x
# 等价于y.backward(torch.ones(len(x)))
y.sum().backward()
x.grad # tensor([0., 2., 4., 6.])
概率
基本概率论
时间概率的预测值: 将事件出现的次数除以投掷的总次数
大数定律: 随着次数的增多,这个估计值会越来越接近真实值
#以投掷骰子为例
import torch
from torch.distributions import multinomial#torch.distributions模块提供了一系列概率分布的实现,包括正态分布、均匀分布、伽马分布等。其中multinomial是用于多项分布的类。
from d2l import torch as d2l
fair_probs = torch.ones([6]) / 6
multinomial.Multinomial(1, fair_probs).sample() # tensor([0., 0., 1., 0., 0., 0.])
multinomial.Multinomial(10, fair_probs).sample() # tensor([5., 3., 2., 0., 0., 0.])
# 现在我们知道如何对骰子进行采样,我们可以模拟1000次投掷。 然后,我们可以统计1000次投掷后,每个数字被投中了多少次。 具体来说,我们计算相对频率,以作为真实概率的估计。
counts = multinomial.Multinomial(1000, fair_probs).sample()
counts / 1000 # 相对频率作为估计值 tensor([0.1550, 0.1820, 0.1770, 0.1710, 0.1600, 0.1550])
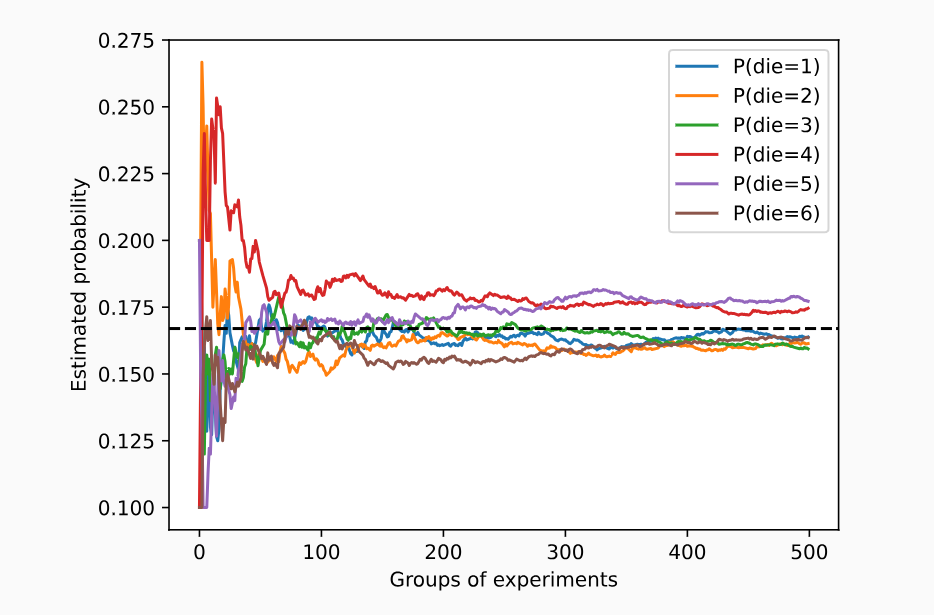
#看这些概率如何随着时间的推移收敛到真实概率。 让我们进行500组实验,每组抽取10个样本。
counts = multinomial.Multinomial(10, fair_probs).sample((500,))
cum_counts = counts.cumsum(dim=0)
estimates = cum_counts / cum_counts.sum(dim=1, keepdims=True)
d2l.set_figsize((6, 4.5))
for i in range(6):
d2l.plt.plot(estimates[:, i].numpy(),
label=("P(die=" + str(i + 1) + ")"))
d2l.plt.axhline(y=0.167, color='black', linestyle='dashed')
d2l.plt.gca().set_xlabel('Groups of experiments')
d2l.plt.gca().set_ylabel('Estimated probability')
d2l.plt.legend();
-
概率论公理
集合S={1,2,3,4,5,6} 称为样本空间(sample space)或结果空间(outcome space), 其中每个元素都是结果(outcome)。 事件(event)是一组给定样本空间的随机结果
概率(probability)可以被认为是将集合映射到真实值的函数
处理多个随机变量
图像包含数百万像素,因此有数百万个随机变量
1. 联合概率
P(A=a,B=b)即A=a,B=b同时发生的概率 P(A=a,B=b)<= P(A=a)
2. 条件概率
并用P(B=b∣A=a)表示它:它是B=b的概率,前提是A=a已发生。
3. 贝叶斯定理
$P(A|B) = \frac {P(B|A) \dot P(A)}{P(B)} $
4. 边际化
为了能进行事件概率求和,我们需要求和法则(sum rule), 即B的概率相当于计算A的所有可能选择,并将所有选择的联合概率聚合在一起:
5. 独立性
如果两个随机变量A和B是独立的,意味着事件A的发生跟B事件的发生无关。 在这种情况下,统计学家通常将这一点表述为A⊥B
期望和方差
一个随机变量的期望 E [ X ] = ∑ x P ( X = x ) E[X] = \sum xP(X=x) E[X]=∑xP(X=x)
方差 V a r [ X ] = E [ ( X − E [ X ] ) ∗ ∗ 2 ] = E [ X ∗ ∗ 2 ] − E [ X ] ∗ ∗ 2 Var[X] = E[(X-E[X])**2] = E[X**2]- E[X]**2 Var[X]=E[(X−E[X])∗∗2]=E[X∗∗2]−E[X]∗∗2
frac {P(B|A) \dot P(A)}{P(B)} $
4. 边际化
为了能进行事件概率求和,我们需要求和法则(sum rule), 即B的概率相当于计算A的所有可能选择,并将所有选择的联合概率聚合在一起:
5. 独立性
如果两个随机变量A和B是独立的,意味着事件A的发生跟B事件的发生无关。 在这种情况下,统计学家通常将这一点表述为A⊥B
期望和方差
一个随机变量的期望 E [ X ] = ∑ x P ( X = x ) E[X] = \sum xP(X=x) E[X]=∑xP(X=x)
方差 V a r [ X ] = E [ ( X − E [ X ] ) ∗ ∗ 2 ] = E [ X ∗ ∗ 2 ] − E [ X ] ∗ ∗ 2 Var[X] = E[(X-E[X])**2] = E[X**2]- E[X]**2 Var[X]=E[(X−E[X])∗∗2]=E[X∗∗2]−E[X]∗∗2






















 231
231

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








