深度学习与神经网络复习（自用）

凡ρ1

已于 2025-04-29 15:02:27 修改

阅读量738

点赞数 6

文章标签：深度学习神经网络人工智能

于 2025-04-28 20:03:44 首次发布

本文链接：https://blog.csdn.net/2301_80852187/article/details/147589152

版权

本篇文章用于本人期末复习，也供有需要的朋友学习，如有不对的地方请多多包涵，看到会纠正的。

深度学习概念

1.深度学习定义

深度学习定义：一般是指通过训练多层网络结构对未知数据进行分类或回归

深度学习分类：有监督学习方法——深度前馈网络、卷积神经网络、循环神经网络等；

无监督学习方法——深度信念网、深度玻尔兹曼机，深度自编码器等。

深度学习的思想：

深度神经网络的基本思想是通过构建多层网络，对目标进行多层表示，以期通过多层的高层次特征来表示数据的抽象语义信息，获得更好的特征鲁棒性。

2.深度学习应用

图像处理领域主要应用

图像分类(物体识别)：整幅图像的分类或识别
物体检测：检测图像中物体的位置进而识别物体
图像分割：对图像中的特定物体按边缘进行分割
图像回归：预测图像中物体组成部分的坐标

语音识别领域主要应用

语音识别：将语音识别为文字
声纹识别：识别是哪个人的声音
语音合成：根据文字合成特定人的语音

自然语言处理领域主要应用

语言模型：根据之前词预测下一个单词。
情感分析：分析文本体现的情感(正负向、正负中或多态度类型)。
神经机器翻译：基于统计语言模型的多语种互译。
神经自动摘要：根据文本自动生成摘要。
机器阅读理解：通过阅读文本回答问题、完成选择题或完型填空。
自然语言推理：根据一句话(前提)推理出另一句话(结论)。

综合应用

图像描述：根据图像给出图像的描述句子
可视问答：根据图像或视频回答问题
图像生成：根据文本描述生成图像
视频生成：根据故事自动生成视频

神经网络

人工神经网络（Artificial Neural Networks，简写为ANNs）是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的，并具有自学习和自适应的能力。神经网络类型众多，其中最为重要的是多层感知机。

感知机是神经网络和支持向量机的基础

神经元

神经网络由大量的神经元相互连接而成。每个神经元接受线性组合的输入后，最开始只是简单的线性加权，后来给每个神经元加上了非线性的激活函数，从而进行非线性变换后输出。每两个神经元之间的连接代表加权值，称之为权重（weight）。不同的权重和激活函数，则会导致神经网络不同的输出。

举个手写识别的例子，给定一个未知数字，让神经网络识别是什么数字。此时的神经网络的输入由一组被输入图像的像素所激活的输入神经元所定义。在通过非线性激活函数进行非线性变换后，神经元被激活然后被传递到其他神经元。重复这一过程，直到最后一个输出神经元被激活。从而识别当前数字是什么字。

神经网络的每个神经元如下

神经网络

将单个神经元组织在一起便形成了神经网络。上图中最左边的原始输入信息称之为输入层，最右边的神经元称之为输出层（上图中输出层只有一个神经元），中间的叫隐藏层。

输入层（Input layer），众多神经元（Neuron）接受大量非线形输入讯息。输入的讯息称为输入向量。
输出层（Output layer），讯息在神经元链接中传输、分析、权衡，形成输出结果。输出的讯息称为输出向量。
隐藏层（Hidden layer），简称“隐层”，是输入层和输出层之间众多神经元和链接组成的各个层面。如果有多个隐藏层，则意味着多个激活函数。

激活函数

定义

激活函数（Activation Function），就是在人工神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端，旨在帮助网络学习数据中的复杂模式。

作用

如果不用激活函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合，这种情况就是最原始的感知机（Perceptron）。

使用激活函数能够给神经元引入非线性因素，使得神经网络可以任意逼近任何非线性函数，使深层神经网络表达能力更加强大，这样神经网络就可以应用到众多的非线性模型中。

常用激活函数

常用的非线性激活函数有sigmoid、tanh、relu等等，前两者sigmoid/tanh比较常见于全连接层，为饱和激活函数；后者relu常见于卷积层，为非饱和激活函数

x趋于正无穷，激活函数的导数趋于0，为右饱和；x趋于负无穷，激活函数的导数趋于0，为左饱和。当函数满足左右饱和（即有界），则为饱和函数。

相对于饱和激活函数，使用非饱和激活函数的优势在于两点：

1.非饱和激活函数能解决深度神经网络（层数非常多）带来的梯度消失问题

2.使用非饱和激活函数能加快收敛速度。

Sigmoid

表达式

sigmoid函数的功能是相当于把一个实数压缩至0到1之间。当z是非常大的正数时，g(z)会趋近于1，而z是非常小的负数时，则g(z)会趋近于0。

压缩至0到1有何用处呢？用处是这样一来便可以把激活函数看作一种“分类的概率”，比如激活函数的输出为0.9的话便可以解释为90%的概率为正样本。

使用情况：用于表示二分类的类别或者用于表示置信度；梯度平滑，便于求导，也防止模型训练过程中出现突变的梯度。

缺点：

容易造成梯度消失。我们从导函数图像中了解到sigmoid的导数都是小于0.25的，那么在进行反向传播的时候，梯度相乘结果会慢慢的趋向于0。这样几乎就没有梯度信号通过神经元传递到前面层的梯度更新中，因此这时前面层的权值几乎没有更新，这就叫梯度消失。除此之外，为了防止饱和，必须对于权重矩阵的初始化特别留意。如果初始化权重过大，可能很多神经元得到一个比较小的梯度，致使神经元不能很好的更新权重提前饱和，神经网络就几乎不学习。
函数输出不是以 0 为中心的，梯度可能就会向特定方向移动，从而降低权重更新的效率
Sigmoid 函数执行指数运算，计算机运行得较慢，比较消耗计算资源。

Tanh

什么情况下适合使用Tanh？

tanh 的输出间隔为 1，并且整个函数以 0 为中心，比 sigmoid 函数更好；
在 tanh 图中，负输入将被强映射为负，而零输入被映射为接近零。

Tanh有哪些缺点？

仍然存在梯度饱和的问题
依然进行的是指数运算

ReLU

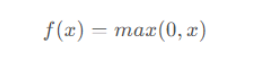
什么情况下适合使用ReLU？

ReLU解决了梯度消失的问题，当输入值为正时，神经元不会饱和
由于ReLU线性、非饱和的性质，在SGD中能够快速收敛
计算复杂度低，不需要进行指数运算

ReLU有哪些缺点？

与Sigmoid一样，其输出不是以0为中心的
Dead ReLU 问题。当输入为负时，梯度为0。这个神经元及之后的神经元梯度永远为0，不再对任何数据有所响应，导致相应参数永远不会被更新

训练神经网络的时候，一旦学习率没有设置好，第一次更新权重的时候，输入是负值，那么这个含有ReLU的神经节点就会死亡，再也不会被激活。所以，要设置一个合适的较小的学习率，来降低这种情况的发生

softmax

softmax把一些输入映射为0-1之间的实数，并且归一化保证和为1，因此多分类的概率之和也为1，最后输出的是每个分类被取到的概率。

优化方法

在机器学习任务中，大部分监督学习算法都会有一个目标函数 (Objective Function),算法对该目标函数进行优化，称为优化算法的过程。

梯度下降

深度学习网络训练过程可以分成两大部分：前向计算过程与反向传播过程。前向计算过程，是指通过我们预先设定好的卷积层、池化层等等，按照规定的网络结构一层层前向计算，得到预测的结果。反向传播过程，是为了将设定的网络中的众多参数一步步调整，使得预测结果能更加贴近真实值。

那么，在反向传播过程中，很重要的一点就是：参数如何更新？或者问的更具体点：参数应该朝着什么方向更新？

显然，参数应该是朝着目标损失函数下降最快的方向更新，更确切的说，要朝着梯度方向更新！

在深度学习中，有三种最基本的梯度下降算法：SGD、BGD、MBGD，他们各有优劣。根据不同的数据量和参数量，可以选择一种具体的实现形式，在训练神经网络是优化算法大体可以分为两类：1）调整学习率，使得优化更稳定；2）梯度估计修正，优化训练速度。

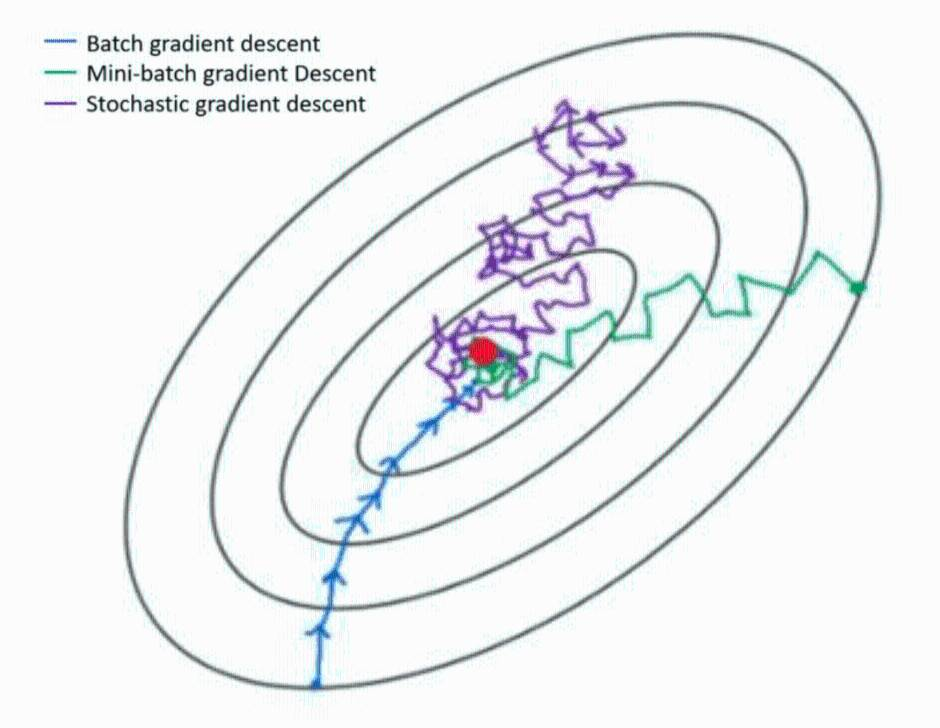
（1）随机梯度下降法 SGD

随机梯度下降法 (Stochastic Gradient Descent，SGD)，每次迭代（更新参数）只使用单个训练样本（ x ( i ) , y ( i ) ）（x^{(i)}, y^{(i)}）（x(i),y(i)），其中x是输入数据，y是标签。因此，参数更新表达式如下：

在这里插入图片描述
优点： SGD 一次迭代只需对一个样本进行计算，因此运行速度很快，还可用于在线学习。

缺点：（1）由于单个样本的随机性，实际过程中，目标损失函数值会剧烈波动，一方面，SGD 的波动使它能够跳到新的可能更好的局部最小值。另一方面，使得训练永远不会收敛，而是会一直在最小值附近波动。（2）一次迭代只计算一张图片，没有发挥GPU并行运算的优势，使得整体计算的效率不高。

（2）批量梯度下降法 BGD

批量梯度下降法 (Batch Gradient Descent，BGD)，每次迭代更新中使用所有的训练样本，参数更新表达式如下：

在这里插入图片描述
优缺点分析：BGD能保证收敛到凸误差表面的全局最小值和非凸表面的局部最小值。但每迭代一次，需要用到训练集中的所有数据，如果数据量很大，那么迭代速度就会非常慢。

（3）小批量梯度下降法 MBGD

小批（3）量梯度下降法 (Mini-Batch Gradient Descent，MBGD)，折中了 BGD 和 SGD 的方法，每次迭代使用 batch_size 个训练样本进行计算，参数更新表达式如下：

在这里插入图片描述
优缺点分析：因为每次迭代使用多个样本，所以 MBGD 比 SGD 收敛更稳定，也能避免 BGD 在数据集过大时迭代速度慢的问题。因此，MBGD是深度学习网络训练中经常使用的梯度下降方法。

上图是BGD和MBGD训练时，损失代价函数的变化图。可见BGD能使代价函数逐渐减小，最终保证收敛到凸误差表面的全局最小值；MBGD的损失代价函数值比较振荡，但最终也能优化到损失最小值。

Adam优化器

Adam 是另一种参数自适应学习率的方法，相当于 RMSprop + Momentum，利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。

损失函数

在机器学习任务中，大部分监督学习算法都会有一个目标函数 (Objective Function),算法对该目标函数进行优化，称为优化算法的过程。例如在分类或者回归任务中，使用损失函数( Loss Function )作为其目标函数对算法模型进行优化。
在BP神经网络中，一般推导中，使用均方误差作为损失函数，而在实际中，常用交叉熵作为损失函数。如下图所示，我们可以清晰地观察到不同的损失函数在梯度下降过程中的收敛速度和性能都是不同的。

均方误差作为损失函数收敛速度慢，可能会陷入局部最优解；
而交叉熵作为损失函数的收敛速度比均方误差快，且较为容易找到函数最优解.

回归损失函数：均方误差损失函数（MSE）等等

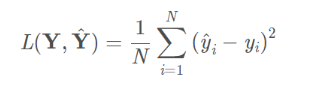
分类损失函数：Logistic损失函数（二分类）

交叉熵损失函数（多分类）

激活函数、损失函数、优化函数的区别

1.激活函数：将神经网络上一层的输入，经过神经网络层的非线性变换转换后，通过激活函数，得到输出。常见的激活函数包括：sigmoid, tanh, relu等。

2.损失函数：度量神经网络的输出的预测值与实际值之间的差距的一种方式。常见的损失函数包括：最小二乘损失函数、交叉熵损失函数、回归中使用的smooth L1损失函数等。

3.优化函数：也就是如何把损失值从神经网络的最外层传递到最前面。如最基础的梯度下降算法，随机梯度下降算法，批量梯度下降算法，带动量的梯度下降算法，Adagrad，Adadelta，Adam等。

CNN

卷积神经网络 – CNN 最擅长的就是图片的处理。它受到人类视觉神经系统的启发。

CNN 特点：

能够有效的将大数据量的图片降维成小数据量。
能够有效的保留图片特征，符合图片处理的原则。

CNN两大核心：

卷积层最主要的两个特征就是局部连接和权值共享，有些地方又叫做稀疏连接和参数共享。

通过卷积操作实现局部连接，这个局部区域的大小就是滤波器filter，避免了全连接中参数过多造成无法计算的情况，
再通过参数共享来缩减实际参数的数量，为实现多层网络提供了可能。

CNN的层级结构

CNN如何识别图像

计算机存储一张标准的“X”图案，然后把需要识别的未知图案跟标准"X"图案进行比对，如果二者一致，则判定未知图案即是一个"X"图案。而且即便未知图案可能有一些平移或稍稍变形，依然能辨别出它是一个X图案。如此，CNN是把未知图案和标准X图案一个局部一个局部的对比。而未知图案的局部和标准X图案的局部一个一个比对时的计算过程，便是卷积操作。卷积计算结果为1表示匹配，否则不匹配。

什么是卷积

对图像（不同的数据窗口数据）和滤波矩阵（一组固定的权重：因为每个神经元的多个权重固定，所以又可以看做一个恒定的滤波器filter）做内积（逐个元素相乘再求和）的操作就是所谓的『卷积』操作，也是卷积神经网络的名字来源。

滤波器的意义

图像和不同的滤波器filter做内积会得到不同的数据输出，如颜色深浅，轮廓

CNN卷积的整体计算过程

在CNN中，滤波器filter（带着一组固定权重的神经元）对局部输入数据进行卷积计算。每计算完一个数据窗口内的局部数据后，数据窗口不断平移滑动，直到计算完所有数据

对于上图左侧而言

输入块的体积大小为32x32x3，可以理解为一栋三层高的楼，每楼一个房间，房间大小为32x32平，如果每一平写一个数字，则有32x32x3个数字，且其
步长stride：决定滑动多少步可以到边缘(很快，你会看到一个步长为2的动图)
填充值zero-padding：在外围边缘补充若干圈0，方便从初始位置以步长为单位可以刚好滑倒末尾位置，通俗地讲就是为了总长能被步长整除

对于上图右侧而言

深度depth：神经元个数，决定输出的depth厚度，同时代表滤波器个数

左边部分，是输入「7*7*3中，7*7代表图像的像素/长宽，3为深度——代表R、G、B 三个颜色通道」，且数据窗口每次移动两个步长取3*3的局部数据，即步长stride=2，另zero-padding=1
中间部分，是两个不同的滤波器Filter w0、Filter w1，对应于两个神经元，即depth=2
最右部分，则是两个不同的输出
卷积操作后，输出的通道数=卷积核的个数

自定义填充
一般是从上下左右四个方向进行填充，且左、右填充的列数p w p_wpw一般相同，上、下填充的行数p h p_hph也应该相同。如下图所示：
在这里插入图片描述
输出尺寸计算公式：

在这里插入图片描述

其中，h,w为原图的高和宽，k是卷积核的尺寸，s是步长。

在TensorFlow2.0中，自定义填充过程中，padding参数的设置格式为：
padding=[ [0，0]，[上，下]，[左，右]，[0，0] ]

# 例如要在上下左右各填充一个单位，实现如下：
layers.Conv2D(48, kernel_size=3, strides=1, padding=[[0,0], [1,1], [1,1], [0,0]])

池化pool层

作用

1.使卷积神经网络抽取特征是保证特征局部不变性。

2.池化操作能降低维度，减少参数数量。

3..池化操作优化比较简单。

常见CNN

LeNet-5

AlexNet

GoogleNet