吴承恩深度学习课程.第一课第三周笔记

本周学习目标

学习实现一个神经网络

神经网络

回忆上一周学习内容主要是对单个神经元进行学习

(这里的y^就是a)

正如第一周所说，神经网络是由多个这样的神经元组成

用到的符号

还是先说明即将会使用到的符号

用上标[m]表示第m层，下标i表示第几个节点

例如

𝑧^[1]代表了第一层的三个节点的z值组成的向量

w^[1]代表了第一层三个节点的w值组成的向量以此类推

第0层，称为输入层输入x的这一层

第一层叫做隐藏层，因为这一层的w，b，a，z都被隐藏了，所以叫做隐藏层

最后一层叫输出层，在图中也就是a^[2]就是输出值也就是y^

神经网络计算过程

正如一开始所说，神经网络是由每个神经元组成的，也就是说，神经网络会不断地重复神经元的计算过程。

这就是a^[1]向量的整个计算过程。在这里

如图所示这里的w维度是（4,3）对于每一个w1^[1]其实都是一个矩阵

这里是a^[1]的计算过程，a^[1]其实是下一层，也就是输出层的输入层

这里的a^[2]就是最终的输出

以上就是单个样本的计算过程

多样本向量化计算过程

对于多个样本，你可能需要一个for循环来遍历这个训练集，现在我们将他向量化来简化这个for循环

如图所示

每一列是一个样本，按行看，每一行是他的第n个隐藏节点。

具体第一步的计算过程如下

w是一个矩阵，x中的每一个样本是一个列向量，相乘结果得到的就是z，具体可以看矩阵点乘的运算过程。

激活函数

以往我们只使用了sigmoid()作为激活函数，但这不一定是最优解，因此我们学习更多的激活函数

tanh函数

如图

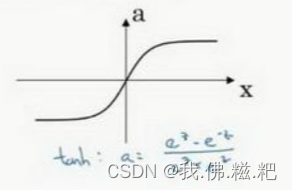
tanh和sigmoid的共同的一个缺点是，当z过大或者过小，他的导数就很小w和b更新的就很慢，最后会影响神经网络运行的速度。

第二个是

RelU函数

RelU = max(0,z)，大多数人都使用这个作为激活函数，缺点是当z为负数的时候z的导数为0

Leaky RelU函数

这个函数是对RelU函数的改进，使得z为负数时也有导数

Leaky RelU = max(0.01z,z)

小结一下四个激活函数

sigmoid函数尽量不用来做激活函数，除非是二分类问题输出层的激活函数，这样使得最后的结果在0到1之间。

当你不知道用当使用什么函数作为激活函数的时候，就使用RelU或者Leaky RelU吧

为什么我们要使用非线性激活函数

与非线性激活函数相反的是线性激活函数，线性激活函数代表了这个函数斜率是不变的，如果隐藏层用线性激活函数，那么得到的结果就是一个线性关系，最终得到的结果可能还不如不添加隐藏层。

神经网络反向传播

之前讲到的都是对神经网络正向传播的笔记。就是求dz

对于四种激活函数，分别讨论他们的导数

sigmoid

tanh

RelU

Leaky RelU

计算这些dz其实就是为了对w和b的梯度下降

这是整个逆向传播的过程。最难以理解的是3.35

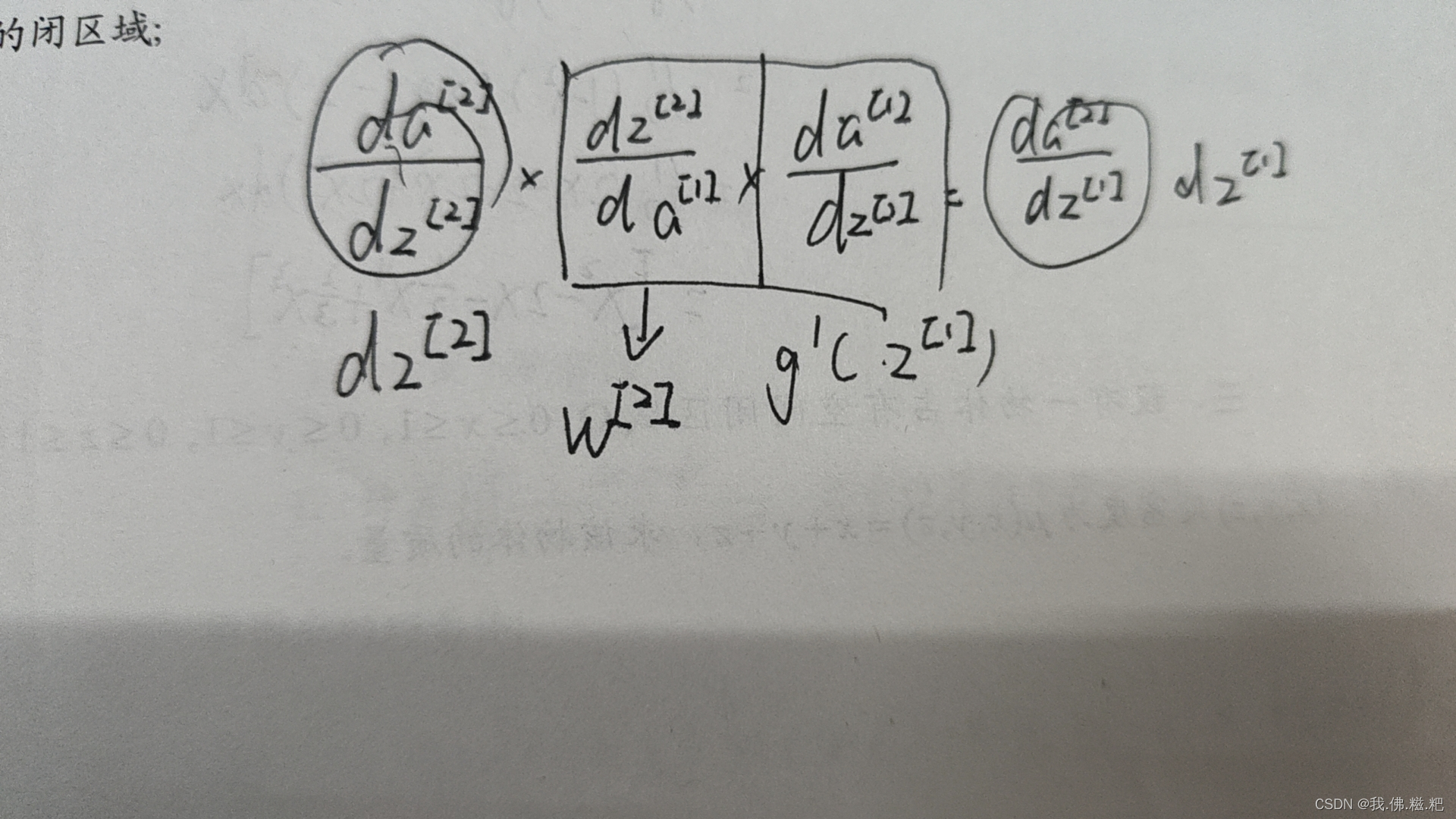
这是我的理解，转置就看他的形状。

随机初始化

在神经网络中，随机初始化是非常重要的，如果一昧的将w1w2初始化为0，会导致隐藏层每一个节点做的事完全相同，使得隐藏层失效。

因此经常将w1w2随机初始化

w=np.random.randa((2,2))*0.01

 *0.01使我们获得一个比较小的一个随机初始值，这样做的好处是解决当你使用tanh和sigmoid时如果步长过长，会使梯度下降的效率降低的问题。0.01不一定是最好的参数，只是在二分类问题以及浅层的神经网络上有比较好的效果。