机器学习——线性判别分析（LDA）推导

LZINC

已于 2024-01-16 16:52:50 修改

阅读量722

点赞数 20

文章标签：机器学习人工智能线性回归数学建模

于 2024-01-16 14:31:11 首次发布

本文链接：https://blog.csdn.net/2301_82047153/article/details/135591390

版权

预备知识

1.点到直线的投影均值与协方差： $X_i$ ， $\mu_i$ ， $\Sigma_i$ 分别为第 $i$ 类示例的集合，均值向量，协方差矩阵。样本中心在直线上的投影为 $w^T\mu_i$ ，样本的协方差为 $w^T\Sigma_iw$ 。

2.矩阵的2-范数：又名欧几里得范数，即向量元素绝对值的平方和再开方， $||X||_2=\sqrt{\sum_{i=1}^{n}\sum_{j=1}^{m}x_{ij}^2}$ ， $||X-Y||_2$ 可以表示矩阵之间的距离。

3.拉格朗日乘数法：对于前面定义中所设的一般目标函数和约束条件组, 应引入辅助函数

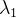
称此函数为拉格朗日函数, 其中 $\lambda_1$ $\lambda_2$ .... $\lambda_m$ 称为拉格朗乘数。

设上述条件极值问题中的函数 $f$ 与 $\varphi_k$ 在在区域 $D$ 上有连续一阶偏导数.。若 $D$ 的内点是该条件极值问题的极值点, 且

则对于m 个常数使得为拉格朗日函数的稳定点即它是如下 $m+n$ 个方程的解。

4.Hessina矩阵：如果 $F$ 的所有二阶导数都存在，则 $F$ 的Hessian矩阵为

$M_F=\begin{bmatrix} \frac{\partial^2 F}{\partial x_1^2} &...& \frac{\partial^2 F}{\partial x_1x_n}\\ ...&...&...\\ \frac{\partial^2 F}{\partial x_nx_1} &...& \frac{\partial^2 F}{\partial x_n^2} \end{bmatrix}$

补充：当Hessina矩阵为正定矩阵时，可知 $F$ 在该点为极小值。

5.矩阵求导法则：设存在矩阵 $m*n$ 矩阵 $Y$ 及 $p$ 维向量 $x=(x_1...x_p)$ ，我们有

$\frac{\partial{Y}}{\partial{x}}=(\frac{\partial{Y}}{\partial{x_1}}...\frac{\partial{Y}}{\partial{x_p}})$

补充：(1) $f(x)=Ax\rightarrow\frac{\partial{f(x)}}{\partial{x^T}}=A$ (2) $f(x)=x^TAx\rightarrow\frac{\partial{f(x)}}{\partial{x}}=Ax+A^Tx$

(3) $f(x)=Ax\rightarrow\frac{\partial Ax}{\partial x}=A^T$

6.正定矩阵：设A为实对称矩阵，若二次型 $X^TAX$ 为正定，即对于任意一组不全为零的实数 $X=(c_1,c_2,...c_n)$ 都有 $X^TAX>0$ 。

补充：当矩阵顺序主子式全部大于0时，可判断该矩阵为正定矩阵。

公式推导

1.对于二分类任务，给定数据集 $D=\{(x_i,y_i)\}_{i=1}^m$ , $y\in\{0,1\}$ , $x=(x_1,....x_n)$ ,学得的LDA模型为 $y=w^Tx$ 。令 $X_i$ ， $\mu_i$ ， $\Sigma_i$ 分别为第 $i\in(0,1)$ 类示例的集合，均值向量，协方差矩阵。我们有LDA模型的 $w$ 为： $w=S_w^{-1}(\mu_0-\mu_1)$ 。

证明：为使得样例投影点尽可能接近，我们让同类样例协方差尽可能小，即 $w^T\Sigma_0w+w^T\Sigma_1w$ 尽可能小。为使得异类样例投影点尽可能远离，我们让类中心之间的距离尽可能大，即 $w^T\mu_0$ 与 $w^T\mu_1$ 之间的2-范数 $||w^T\mu_0-w^T\mu_1||_2^2$ 尽可能大。则我们得到最大化目标：

$J=\frac{||w^T\mu_0-w^T\mu_1||_2^2}{w^T\Sigma_0w+w^T\Sigma_1w} \\=\frac{\sum_{i=1}^n(w_i\mu_{0i}-w_i\mu_{1i})^2}{w^T(\Sigma_0w-\Sigma_1w)} \\=\frac{\sum_{i=1}^nw_i^2(\mu_{0i}-\mu_{1i})^2}{w^T(\Sigma_0w-\Sigma_1w)} \\=\frac{w^T(\mu_0-\mu_1)(\mu_0-\mu_1)^Tw}{w^T(\Sigma_0w-\Sigma_1w)}$

我们设类内散度矩阵 $S_w$ ：

$S_w=\Sigma_0+\Sigma_1 \\=\sum_{x\in X_0}(x-\mu_0)(x-\mu_0)^T+\sum_{x\in X_1}(x-\mu_1)(x-\mu_1)^T$

设类间散度矩阵 $S_b$ ：

$S_b=(\mu_0-\mu_1)(\mu_0-\mu_1)^T$

则我们有：

$J=\frac{w^TS_bw}{w^TS_ww}$

由于我们不关注 $w$ 其大小，只关心其方向，通过 $w$ 的长度变换，并不影响其方差，均值的取值，因此，该式可等价为条件极值问题：

$min -w^TS_bw \\s.t. w^TS_ww=1$

我们由拉格朗日乘子法，作拉格朗日函数： $L=-w^TS_bw +\lambda (w^TS_ww-1)$ ，我们对其求导有：

$L_\lambda= w^TS_ww-1=0$

$L_w=-(S_b^T+S_b)w +\lambda (S_w^T+S_w)w=0$

则我们有 $(S_b^T+S_b)w =\lambda (S_w^T+S_w)w$ 。由于 $S_b=S_b^T,S_w=S_w^T$ 我们有 $2S_bw =2\lambda S_ww$ 。由于 $(\mu_0-\mu_1)^Tw$ 为常数，因此 $S_bw$ 的方向为 $(\mu_0-\mu_1)$ ，那么我们有 $S_bw =\alpha(\mu_0-\mu_1)$ ，则我们有 $\alpha(\mu_0-\mu_1)=\lambda S_ww$ ， $\frac{\alpha}{\lambda }S_w^{-1}(\mu_0-\mu_1)=w$ 成立。由于不关心 $w$ 其大小，只关心其方向，所以其大小可以任意取值，我们取 $\frac{\alpha}{\lambda }=1$ ，则有 $S_w^{-1}(\mu_0-\mu_1)=w$ 。{该部分推导存在问题(我们对 $L$ 求二阶偏导有：

$L_{\lambda\lambda}=0$ , $L_{w\lambda }=L_{\lambda w}=(S_w+S_w^T)w$ , $L_{ww}=-(S_b^T+S_b)+\lambda (S_w^T+S_w)$

我们构造 $L$ 的Hessina矩阵：

$L_H=\begin{bmatrix} -(S_b^T+S_b)+\lambda (S_w^T+S_w)&(S_w+S_w^T)w \\ (S_w+S_w^T)w& 0\\ \end{bmatrix}$

代入 $S_w^{-1}(\mu_0-\mu_1)=w$ 及 $(S_b^T+S_b)w =\lambda (S_w^T+S_w)w$ ，显然有 $L_H$ 为正定矩阵，我们可知 $S_w^{-1}(\mu_0-\mu_1)=w$ 为极小值点，又由于仅有一个极小值点可知为最小值点。)}证毕。

2.对于多分类任务，给定数据集 $D=\{(x_i,y_i)\}_{i=1}^m$ , $y\in\{0,1,...N\}$ , $x=(x_1,....x_n)$ ,学得的LDA模型为 $y=w^Tx$ 。令 $X_i$ ， $\mu_i$ ， $\Sigma_i$ 分别为第 $i\in\{0,1,...N\}$ 类示例的集合，均值向量，协方差矩阵。我们有LDA模型的 $w$ 的闭式解为：

$S_w^{-1}S_b$ 的 $d'$ 个最大非零广义特征值所对应的特征向量组成的矩阵。

证明：定义 $S_t=S_b+S_w=\sum_{i=1}^m(x_i-\mu)(x_i-\mu)^T$ ， $\mu$ 为所有示例的均值向量。定义 $S_w=\sum_{i=1}^mS_{w_i}$ 即每个类别的散度矩阵之和，其中 $S_{w_i}=\sum_{x\in X_i}(x-\mu_i)(x-\mu_i)^T$ 。

则我们有：

我们设 $W=(w_1.w_2,...w_{N-1})$ 为一个投影矩阵，其中 $w_i\in R^{d*1}$ 为 $d$ 行1列的列向量。我们为了使得同类样例协方差尽可能小，即 $tr(W^TS_bW)=\sum_{i=1}^{N-1} w_i^2S_bw_i$ 尽可能小。为使得异类样例投影点尽可能远离，我们让类中心之间的距离尽可能大，即 $tr(W^TS_wW)=\sum_{i=1}^{N-1} w_i^2S_ww_i$ 尽可能大。则我们有使得 $J=\frac{tr(W^TS_bW)}{tr(W^TS_wW)}$ 最小即可。

该问题等价于条件极值：

$min\, -tr(-W^TS_bW) \\s.t.\, \, \, \, \, \, tr(W^TS_wW)=1$

我们使用拉格朗日乘数法，构造拉格朗日方程为 $L=-tr(W^TS_bW )+\lambda (tr(W^TS_wW)-1)$ 。由 $S_b=S_b^T$ 与 $S_w=S_w^T$ ，我们对 $L$ 求偏导使值为0有：

$L_w=-(S_b^T+S_b)W +\lambda (S_w^T+S_w)W=-2S_bW+2\lambda S_wW=0$

于是我们有 $2S_bW=2\lambda S_wW$ ，则LDA模型的 $w$ 的闭式解 $S_w^{-1}S_b$ 的 $d'$ 个最大非零广义特征值所对应的特征向量组成的矩阵成立。证毕。

LZINC

关注

20
点赞
踩
17

收藏

觉得还不错? 一键收藏
打赏
3
评论
机器学习——线性判别分析（LDA）推导

1.点到直线的投影均值与协方差：分别为第类示例的集合，均值向量，协方差矩阵。样本中心在直线上的投影为，样本的协方差为。2.矩阵的2-范数：又名欧几里得范数，即向量元素绝对值的平方和再开方，可以表示矩阵之间的距离。3.拉格朗日乘数法：对于前面定义中所设的一般目标函数和约束条件组, 应引入辅助函数称此函数为拉格朗日函数, 其中....称为拉格朗乘数。设上述条件极值问题中的函数与在在区域上有连续一阶偏导数.。若的内点是该条件极值问题的极值点, 且则对于m 个常数使得。
复制链接

扫一扫