机器学习——降维算法（MDS，PCA，LLE）推导

LZINC

于 2024-02-05 00:18:32 发布

阅读量1.7k

点赞数 37

文章标签：机器学习算法人工智能数学建模

本文链接：https://blog.csdn.net/2301_82047153/article/details/136026644

版权

本文详细介绍了拉格朗日乘数法在求解约束优化问题中的应用，包括矩阵求导法则，以及矩阵2-范数的概念。重点讨论了MDS、PCA和LLE三种降维算法的原理、证明过程和优化方法，展示了这些在数据处理中的实际应用。

摘要由CSDN通过智能技术生成

预备知识：

1.拉格朗日乘数法：对于前面定义中所设的一般目标函数和约束条件组, 应引入辅助函数

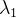
称此函数为拉格朗日函数, 其中 $\lambda_1$ $\lambda_2$ .... $\lambda_m$ 称为拉格朗乘数。

设上述条件极值问题中的函数 $f$ 与 $\varphi_k$ 在在区域 $D$ 上有连续一阶偏导数.。若 $D$ 的内点是该条件极值问题的极值点, 且

则对于m 个常数使得为拉格朗日函数的稳定点即它是如下 $m+n$ 个方程的解。

2.矩阵求导法则：

矩阵求导法则：设存在矩阵 $m*n$ 矩阵 $Y$ 及 $p$ 维向量 $x=(x_1...x_p)$ ，我们有

$\frac{\partial{Y}}{\partial{x}}=(\frac{\partial{Y}}{\partial{x_1}}...\frac{\partial{Y}}{\partial{x_p}})$

补充：(1) $f(x)=Ax\rightarrow\frac{\partial{f(x)}}{\partial{x^T}}=A$ (2) $f(x)=x^TAx\rightarrow\frac{\partial{f(x)}}{\partial{x}}=Ax+A^Tx$

(3) $f(x)=Ax\rightarrow\frac{\partial Ax}{\partial x}=A^T$

3.矩阵的2-范数：又名欧几里得范数，即向量元素绝对值的平方和再开方， $||X||_2=\sqrt{\sum_{i=1}^{n}\sum_{j=1}^{m}x_{ij}^2}$ ， $||X-Y||_2$ 可以表示矩阵之间的距离。

公式推导：

1.MDS算法：假定m个属性在原始空间的距离矩阵为： $D\in R^{m \times m}$ ，其 $i$ 行 $j$ 列的元素 $dist_{ij}$ 为样本 $x_i$ 到 $x_j$ 的距离。我们假设样本在 $d'$ 维空间的表示 $Z\in d'\times m$ ，且任意两个样本在 $d'$ 维空间中距离为 $||z_i-z_j||=dist_{ij}$ 。

证明：我们令 $B=Z^TZ$ 为降维后的内积矩阵， $b_{ij}=z_i^Tz_j$ ，我们有：

$dist_{ij}=||z_i-z_j||^2 \\=(z_i-z_j)^T(z_i-z_j) \\=(z_i^T-z_j^T)(z_i-z_j) \\=z_i^Tz_i+z_j^Tz_j-z_i^Tz_j-z_j^Tz_i \\=b_{ii}+b_{jj}-b_{ij}-b_{ji} \\=b_{ii}+b_{jj}-2b_{ij}$

我们假设降维后样本Z被中心化： $\sum_{i=1}^mz_i=0$ 。我们有：

$\sum_{i=1}^mb_{ij}=\sum_{i=1}^mz_i^Tz_j=z_j\sum_{i=1}^mz_i^T=0$

$\sum_{j=1}^mb_{ij}=\sum_{j=1}^mz_i^Tz_j=z_i\sum_{j=1}^mz_j^T=0$

那么我们有：

$\sum_{i=1}^mdist_{ij}^2=\sum_{i=1}^m(b_{ii}+b_{jj}-2z_i^Tz_j)\\=tr(B)+mb_{jj}-\sum_{i=1}^m2z_i^Tz_j\\=tr(B)+mb_{jj}$

同理，我们有：

$\sum_{j=1}^mdist_{ij}^2=tr(B)+mb_{ii}$

$\sum_{i=1}^m\sum_{j=1}^mdist_{ij}^2=2m tr(B)$

其中 $tr(B)=\sum_{i=1}^m||z_i||^2$ 。

我们令：

$dist_{i *}^2=\frac{1}{m}\sum_{j=1}^mdist^2_{ij}$

$dist_{*j}^2=\frac{1}{m}\sum_{i=1}^mdist^2_{ij}$

$dist_{**}^2=\frac{1}{m^2}\sum_{i=1}^m\sum_{j=1}^mdist^2_{ij}$

我们有：

$b_{ij}=\frac12(b_{ii}+b_{jj})-dist_{ij}^2 \\=\frac1{2m}(\sum_{j=1}^mdist_{ij}^2-tr(B)+\sum_{j=1}^mdist_{ij}^2-tr(B))-dist_{ij}^2 \\=\frac1{2m}(\sum_{j=1}^mdist_{ij}^2+\sum_{j=1}^mdist_{ij}^2-2tr(B))-dist_{ij}^2 \\=-\frac{1}{2}(dist_{ij}^2-dist_{i *}^2-dist_{*j}^2+dist_{**}^2)$

我们对 $B$ 进行特征值分解， $B=VAV^T$ ，其中 $A=diag(\lambda_1,...,\lambda_d)$ ，我们取其非零的特征向量，我们有： $A^*=diag(\lambda_1^*,...,\lambda_d^*)$ ，对应特征向量为 $V^*$ 。

$Z=A^{*\frac 12}V^*$

在降维过程中，距离可不必完全相等，于是我们可以取前几个最大特征值来构成对角矩阵： $\overline A=diag(\lambda_1,...,\lambda_{d"})$ ， $\overline{V}$ 为对应特征向量， $Z=\overline A^{\frac 12}\overline V$ 。

2.主成分分析（PCA）算法：

证明：假设数据样本进行了中心化， $\sum_{i=1}^mx_i=0$ ，假设投影变换后的新坐标系为 $\{w_1,w_2,...,w_d\}$ ， $w_i$ 为标准向量基，将 $x_i$ 降低维度到 $z_i=(z_{i1};z_{i2};...;z_{id'})$ ，其中 $z_{ij}=w_j^Tx_i$ 是 $x_i$ 在低维坐标系下的第j维的坐标。基于 $z_i$ 重构 $x_i$ 我们有 $\widehat{x_i}=\sum_{j=1}^{d'}z_{ij}w_j$

我们设 $W=(w_{1,w_2,...,w_d})$ ，计算原样本点 $x_i$ 与重构的样本点 $\widehat x_i$ 距离：

我们由最近重构性，将 $-tr(W^T(\sum_{i=1}^mx_i^Tx_i)W)=-tr(W^TX^TXW)$ 最小化，由于 $w_i$ 为标准正交基，我们有 $W^TW=E$ 。我们有以下目标优化：

$min_W-tr(W^T(\sum_{i=1}^mx_i^Tx_i)W) \\s.t.W^TW=E$

我们使用拉格朗日数乘法构造拉格朗日函数 $L=-tr(W^TX^TXW) +\lambda (W^TW+E)$ ，其中 $\lambda=(\lambda_1, \lambda_{2},...,\lambda_n)$ 。我们将其对 $W$ 求导有：

$\frac{\partial L}{\partial W}\\=\frac{\partial (-tr(W^TX^TXW) +\lambda (W^TW+E))}{\partial W}\\=-(2XX^TW)+2\lambda W$

我们有使之为0，有 $XX^TW=\lambda W$ ，由此我们有 $XX^Tw_i=\lambda_i w_i$ 。我们对协方差矩阵 $XX^T$ 进行特征值分解，将求得的特征值进行排序： $\lambda_d \leq \lambda_{n-1}\leq...\leq\lambda_1$ 。我们取前 $d'$ 个特征向量对应特征向量构成 $W=(w_1,w_2,...,w_{d'})$ 即为主成分分析的解。

3.LLE算法：

证明：假定样本点 $x_i$ 的坐标能通过它的邻域样本点 $x_j$ ， $x_k$ ， $x_l$ 。我们为每个 $x_i$ 找出近邻下标集 $Q_i$ ，计算出基于 $Q_i$ 中的样本点进行线性重构系数 $w_i$ ：

$min_{w_1,w_2,...,w_m}\sum_{i=1}^m||x_i-\sum_{j\in Q_i}w_{ij}x_j|| \\\sum_{j\in Q_i}w_{ij}=1$

我们有：

其中 $w_i=(w_{iq^1_i},w_{iq^2_i},...,w_{iq^n_i})$ ， $X_i=(x_i-x_{iq^1_i},x_i-x_{iq^2_i},...,x_i-x_{iq^n_i})$ 。

我们有约束条件为： $\sum_{j\in Q_i}w_{ij}=w_i^TI=1,I=(1,1,1,...,1)$ 。

我们可以得到最终的优化方程：

$min\sum_{i=1}^mw_i^TW^TWw_i \\s.t.w_i^TI=1$

我们对其使用拉格朗日乘数法构造拉格朗日函数有： $L=\sum_{i=1}^mw_i^TW^TWw_i +\lambda( w_i^TI-1)$ 。

我们将其对 $w_i$ 求导并使之等于0有：

$X_i^TX_iw_i=-\frac{1}{2}\lambda I \\w_i=-\frac12\lambda ({X_i^TX_i})^{-1}I$

我们对其乘以 $I^T$ 有:

$I^Tw_i=-\frac12\lambda I^T({X_i^TX_i})^{-1}I=1 \\-\frac12\lambda=\frac{1}{I^T({X_i^TX_i})^{-1}I}$

将 $-\frac12\lambda=\frac{1}{I^T({X_i^TX_i})^{-1}I}$ 代入到 $w_i=-\frac12\lambda ({X_i^TX_i})^{-1}I$ 有： $w_i=\frac{\lambda ({X_i^TX_i})^{-1}I}{I^T({X_i^TX_i})^{-1}I}$ 。我们设 $C_{jk}=(x_i-x_{iq_i^j})^T(x_i-x_{iq_i^k})$ ，那么我们有： $w_{ij}=\frac{\sum_{k\in Q_i}C_{jk}^{-1}}{\sum_{l,k\in Q_i}C_{ls}^{-1}}$ 。

相应的低维空间中保持 $w_i$ 不变，则我们可以通过以下式求得对应的低维坐标 $z_i$ :

$min_{z_1,z_2,...,z_m}\sum_{i=1}^m||z_i-\sum_{j\in Q_i}w_{ij}z_j||$ 。

我们设 $M=(I-W)^T(I-W)$ ，则有：

最终得到我们的优化方程：

$min_Z tr(ZMZ^T) \\Z^TZ=E$

参考文献：

第10章降维与度量学习 (datawhalechina.github.io)https://datawhalechina.github.io/pumpkin-book/#/chapter10/chapter10

西瓜书：PCA数学推导_pca西瓜书-CSDN博客https://blog.csdn.net/weixin_45963617/article/details/107426075

LZINC

关注

37
点赞
踩
29

收藏

觉得还不错? 一键收藏
打赏
2
评论
机器学习——降维算法（MDS，PCA，LLE）推导

1.拉格朗日乘数法：对于前面定义中所设的一般目标函数和约束条件组, 应引入辅助函数称此函数为拉格朗日函数, 其中....称为拉格朗乘数。设上述条件极值问题中的函数与在在区域上有连续一阶偏导数.。若的内点是该条件极值问题的极值点, 且则对于m 个常数使得为拉格朗日函数的稳定点即它是如下个方程的解。2.矩阵求导法则：矩阵求导法则：设存在矩阵矩阵及维向量，我们有补充：(1)(2)(3)3.矩阵的2-范数：又名欧几里得范数，即向量元素绝对值的平方和再开方，
复制链接

扫一扫