如何理解施密特（Schmidt）正交化

        如题，在今天学习线性代数时，觉得书上对于施密特正交化部分的解释还不够明了（作者用的是同济版的线性代数，对于农科学生来说可能不够明了），于是就想到能不能用通俗易懂的方法把这个知识呈现出来，于是就有了这篇文章，话不多说，直接进入正题

一.施密特正交化

        设  是向量空间  的一个基，要求  的一个标准正交基。这也就是要找一组两两正交的单位向量  与  等价。这样一个问题，称为把基  标准正交化。

我们可以用以下方法把  标准正交化：取

然后把它们单位化，即取

就是  的一个标准正交基。

上述从线性无关向量组  导出正交向量组  的过程称为施密特正交化。

二.“通俗”理解施密特正交化

        在开始之前，默认你已经知道了内积等学习施密特正交化需要的一些基本知识

        我知道，定义总是晦涩难懂的，想要通俗的理解就要从别的角度去思考，而对人类来说，图形恰恰是理解记忆的好方式，下面我将以数形结合的方式来带你了解这个定理。

余弦定理与向量距离

        在平面直角坐标系中，假设有向量  ,如图（懒得作图了，顺便展示一下子画工）

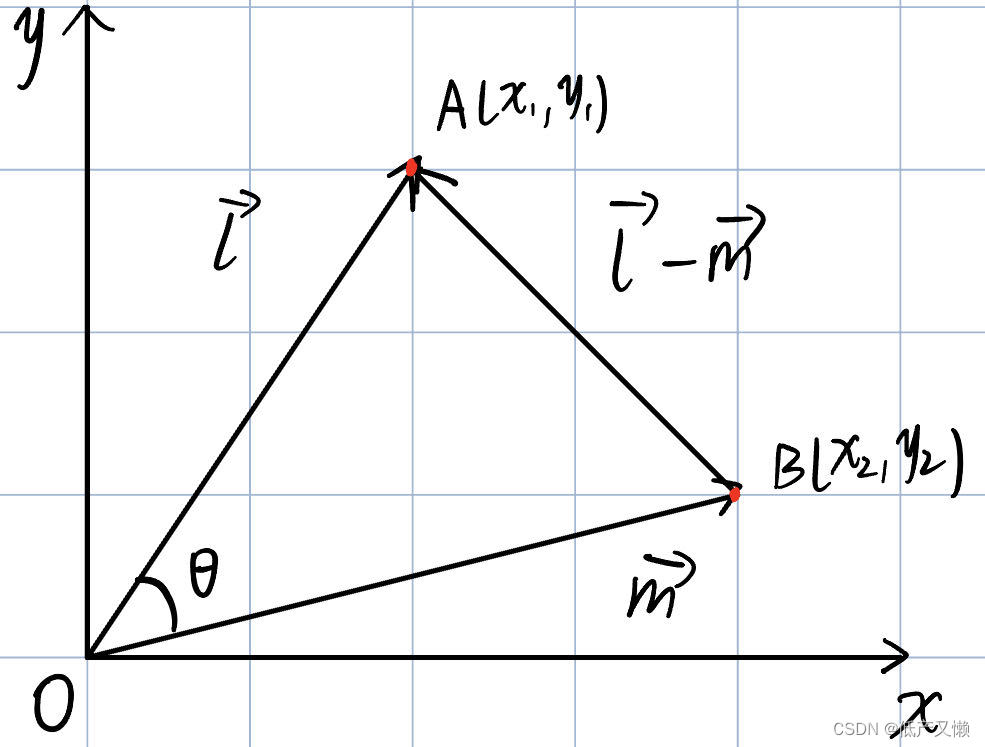
在这三角形AOC中，对A,B距离的平方，有

        余弦定理：

        坐标：

显然，两式中后一项相等

即，向量的内积为

正文

        现在，回到公式中，我们不妨把问题简化一下，假设向量空间是二维空间

        设在二维空间中，有正交向量  ，任意向量  ，由正交向量性质可知，一对正交向量必然共面且垂直，而平面直角坐标系的坐标轴恰恰具有这个性质，那么由  ，不妨建在所在的平面建立平面直角坐标系，并设任意向量与y轴重合，如图：

        回到施密特正交化的目的，其意义就是将一组任意向量通过初等变换化为正交向量，而向量的初等变换正是向量在直角坐标系中的坐标变换，

        即，其目的就是（二维平面）将一对向量，使其中一个向量与x或y轴重合，另一向量通过变换使其与另一坐标轴重合，这样就达到了正交化

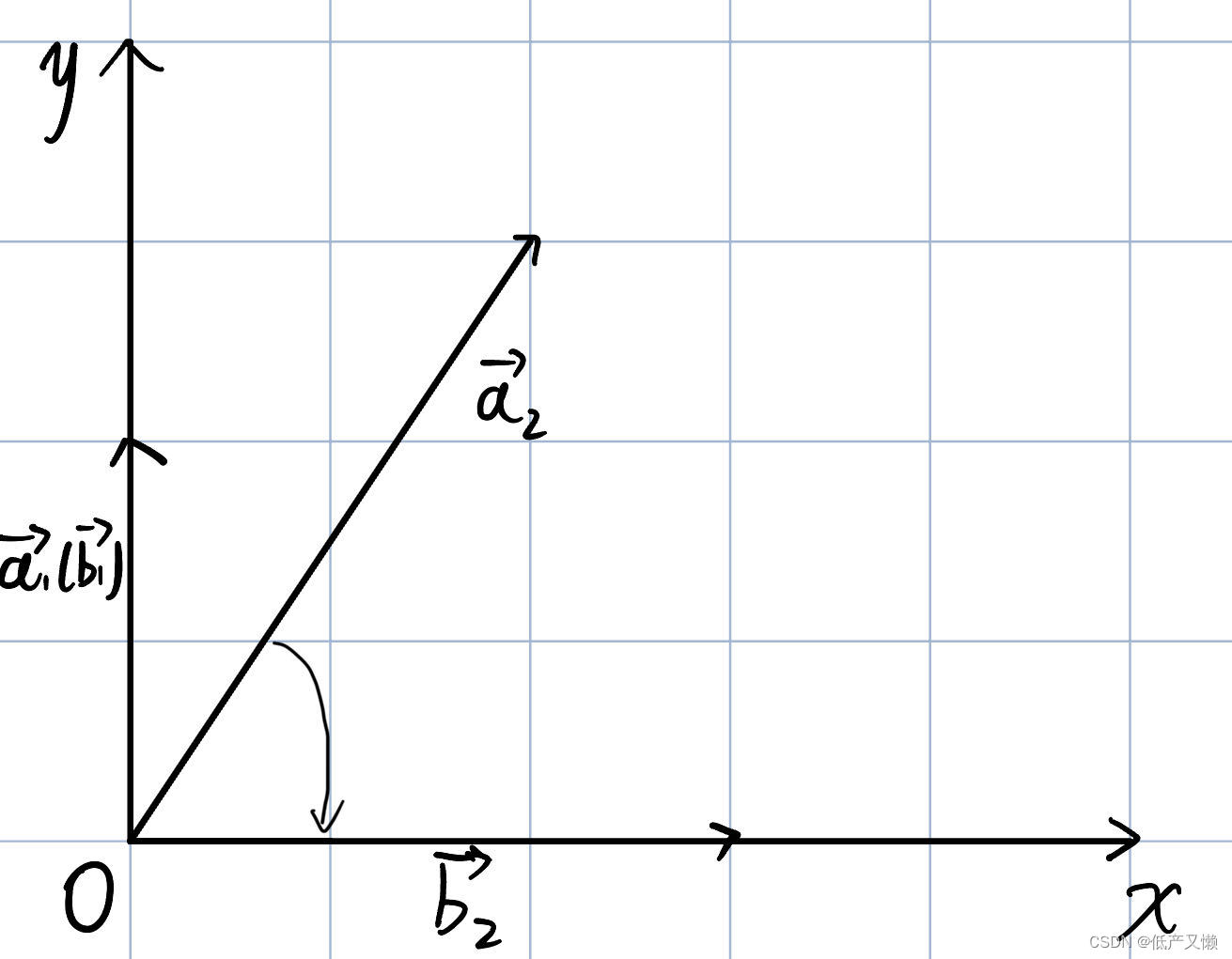
明白了其中的原理之后，我们再回到式子中，来看看如何理解这冗杂的东西

还是在二维平面中，有

第一个式子不做过多解释，正是前文所提的“设任意向量与y轴重合”的情况

我们来仔细研究第二个式子，首先将式子写为

其中 ，为常数

不难发现，式子右侧部分的几何意义如下图：

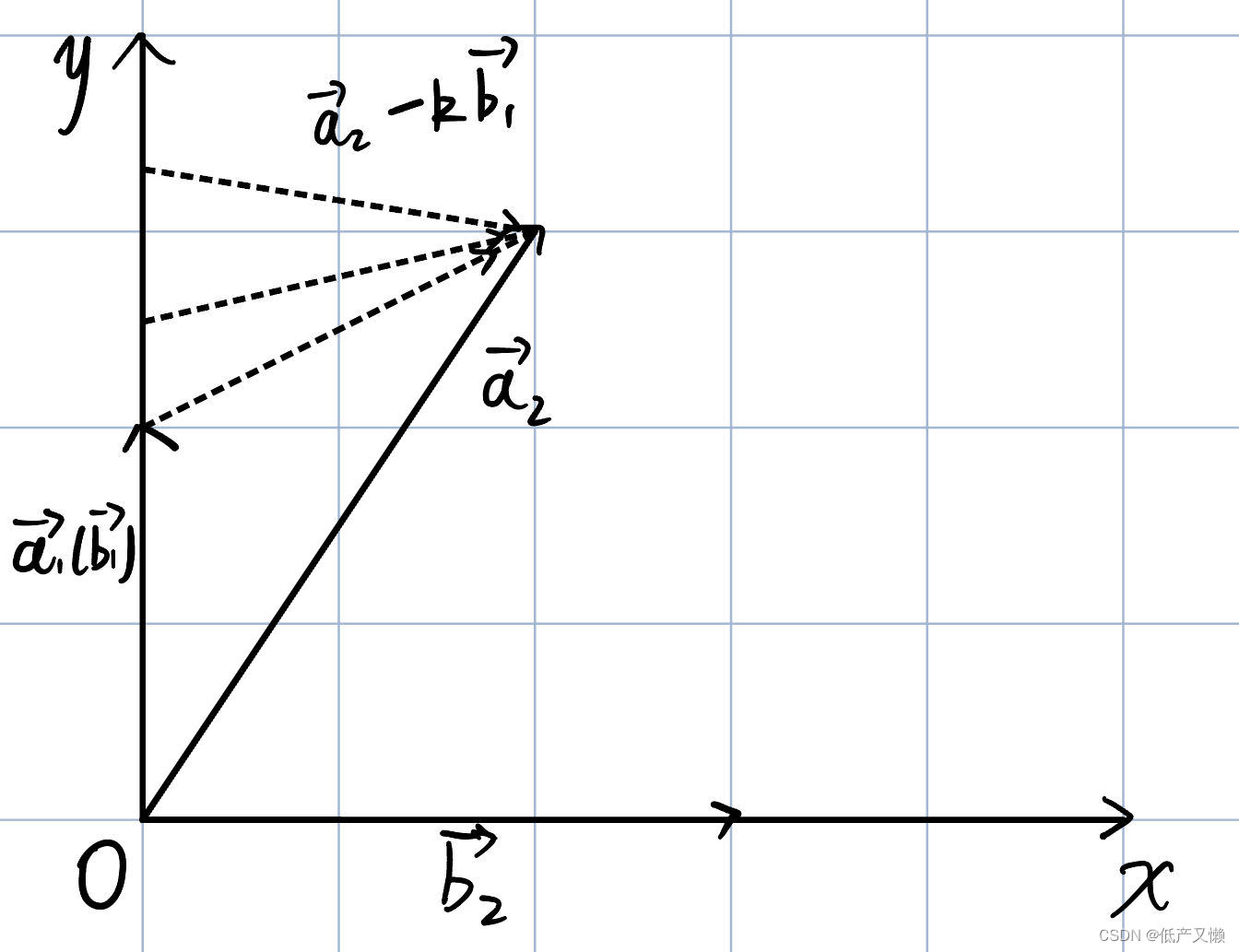
显然  的作用就是找到一个合适的向量  使之与x轴平行

现在我们来研究系数  的意义

由上文中通过两向量推到的公式：

结合一些简单的变形，不难得到

其中  则为单位化后的 ，即与  共线的单位向量

则  的表达式为

其实到这里就已经很明显了， 的意义就是先将  单位化，再将其长度化为与向量  在y轴上的投影等长，这样就解释了为什么  可以将  放缩到合适的长度，使得  使之与x轴平行。

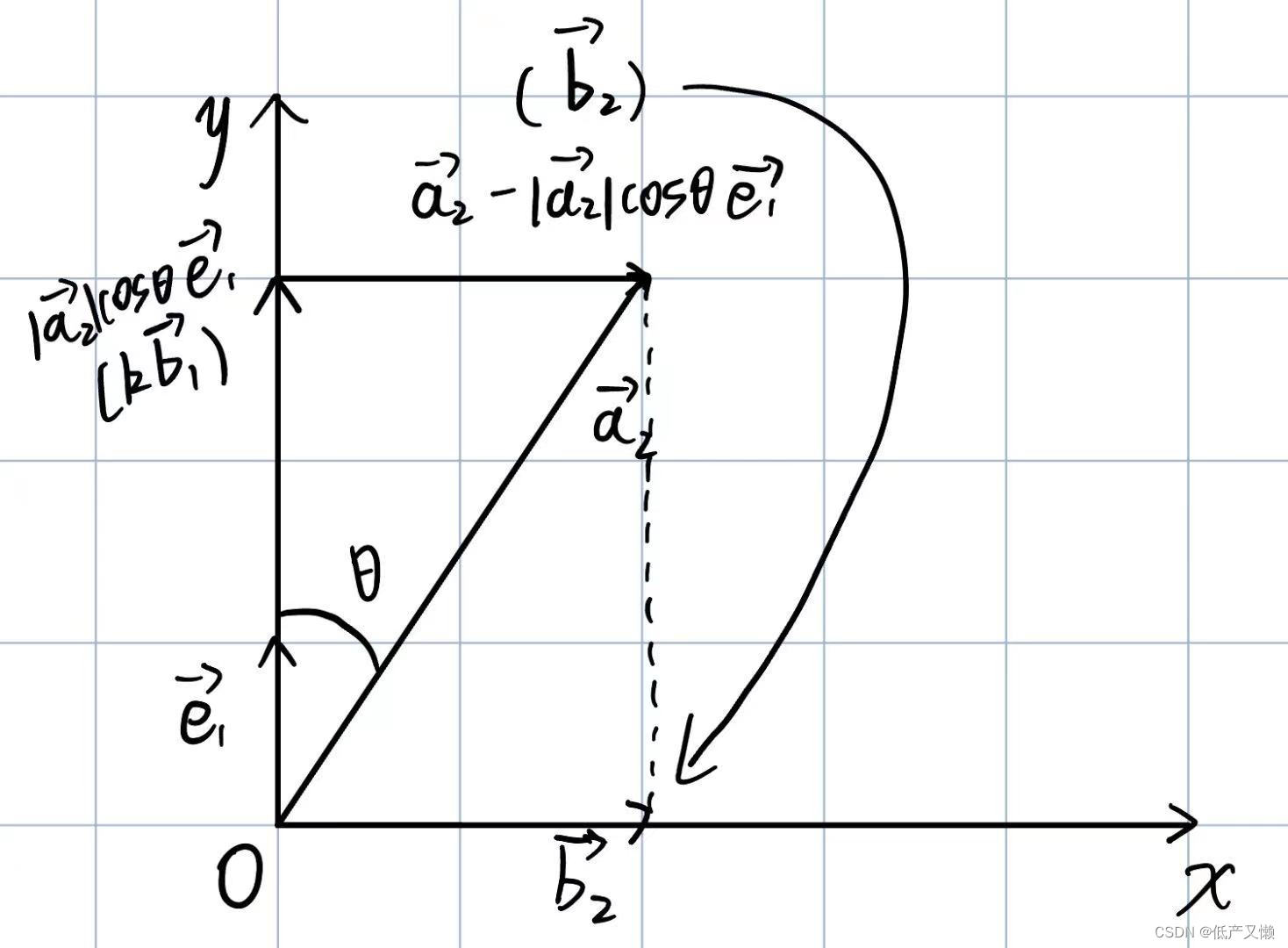
至此，在二维平面上的施密特变换就已经完毕

        在三维平面时规律也是如此，你可以把它通俗的理解为有一个鸡爪子，如果选定了一个脚趾作为“参考”，那么正交化鸡爪子的过程就是将另外一个掰到与参考脚趾垂直，将最后一个掰到与前面两个垂直

        如若上升到n维，作者暂时还没想好怎样通俗理解，目前就当作二维的推广来记忆即可，如果有更好的通俗易懂的方法，欢迎评论交流！

ps：作者数学不是很好，可能有些部分不严谨，敬请指正！