低阶行列式
行列式:行数=列数,边界有两条竖线的算式,算式类型是数。
例题
行列式的几何意义
得出结论如下:
行列式中向量线性相关的说法
行列式的唯一性判断
低阶行列式的计算
行列式的定义(第二类行列式定义)
全排列和对换
全排列:把n个不同的元素排成一列,叫做这n个元素的全排列。
n个不同元素的所有排列的种数,通常用Pn表示。
逆序与逆序数
逆序:若存在一个大数排在一个小数前面,则这一个对数构成“一个逆序”。
逆序数:逆序的总个数
奇偶排列:逆序数为"奇"称为奇排列,逆序数为"偶"称为偶排列
对换
行列数的原始定义
行列式的原始定义:每一项均取自不同行不同列n个元素的乘积的“代数和”,共有n!项,其正负由“行标逆序数+列标逆序数”的奇偶性决定
定义的应用
判断行列式的符号
计算行列式

几类重要的行列式
逆序数的首项和末项:
从第n列到第1列有n-1个逆序,从第n-1列到第2列有n-2个逆序,一直这么递推
行列式的性质
性质一 行列式的转置
性质二 互换性质
一组排列中,若两个数对换,则排列的奇偶性发生改变,所以n!项的每一项,正负均发生改变所以行列式必然反号
互换性质说明两行(列)相同,该行列式等于0
可得出推论:推论若行列式在两行(列)相同,其值为0。
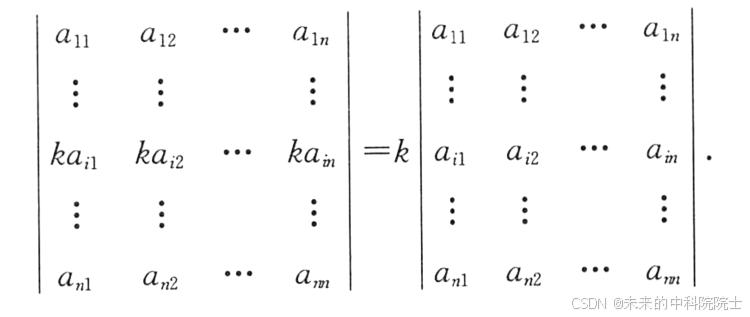
性质三 倍乘性质
注意:是对某一行(列)乘k=k乘原行列式。
也可以用向量的思路来理解:
k乘某一行,相当于将一条边延长k倍,所以行列式也扩大k倍
性质四 可拆性质

性质五 倍加性质

例题


行列式展开(行列式第三定义)
低阶行列式的计算要比高阶行列式的计算要简便,我们考虑用低阶行列式来表示高阶行列式的问题,为此引进了余子式和代数余子式的概念
行列式展开定理
需要注意:按行展开时,只看当行的,但当写代数余子式中的行列式是,要删去当行和当列的部分。
例题
替换法则

替换法则的推论

例题
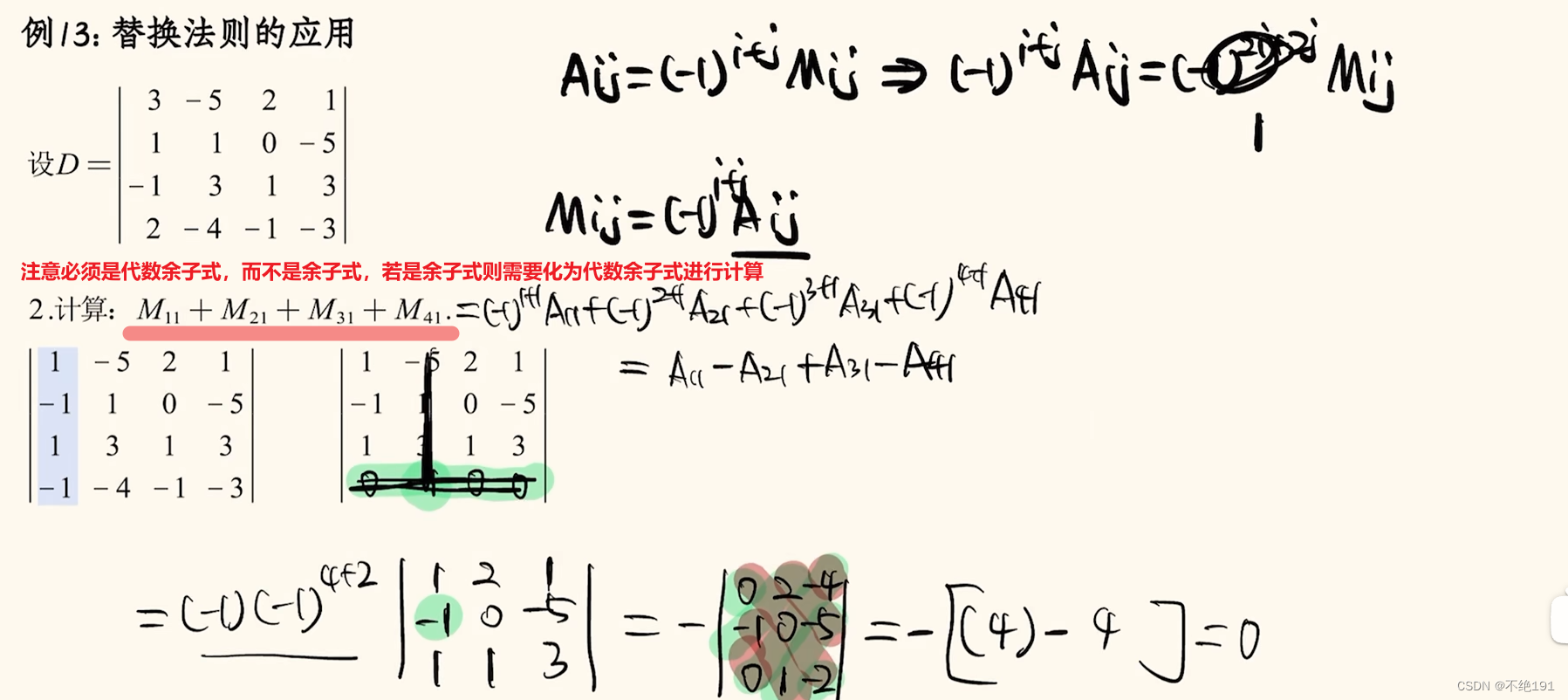

















































 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








