线性相关、线性无关、线性表示的相关概念
n维向量与n维空间的理解
向量长度为多长,就称作几维向量。n维空间要看向量组中有多少n维独立向量的独立线性组合——am能被an-1,an-2……a1线性表示,该向量组最多张成n-1维空间。
线性组合的理解
线性相关、线性无关的概念理解
线性相关:向量组内部至少存在一个向量可以用其余向量线性表示。
线性无关:向量组内部任何一个向量都不可以用其余向量线性表示。
秩与线性相关的概念
线性无关且能表示出整体向量组的部分向量组叫做极大无关组
从向量个数来理解秩和线性相关(无关)
从向量维度来理解秩和线性相关(无关)
综上,我们可以得知:增加向量个数——提高相关性
增加向量维度——提高无关性
线性相关(无关)的隐藏条件
同为n维向量,B不能被A表示,说明线性组合A为低维,说明线性组合中有线性相关量
B1,B2同为n维向量,不能被n-1维空间表示,且与n-1维空间正交,说明B1,B2在同一维度的同一直线上,所以线性相关
向量组中线性相关,但具体相关情况不得知的话有情况如下:
B与am的线性组合线性相关,与am-1线性无关,am也与am-1与B的线性组合相关
两个向量组均线性无关,其线性相关情况
正交与线性无关的关系以及注意事项
单个向量作为向量组的情况(单个向量线性相关/无关)
线性相关的七大证明定义
1、定义法
2、原向量组线性无关,加入一个向量后线性相关,加入的向量可被该向量组线性表示
3、一个多的向量组可被另一个少的向量组线性表示,多的向量组线性相关
其等价命题如下:
即低维向量组(低维空间)可以被高维向量组(高维空间)表示,向量组b可以被a表示,说明b相较于a低维,所以b的数量小于a。
4、向量组线性相关,其充要条件为齐次方程组必有非零解
证明如下:
其等价命题:m个n维列向量α1,a2 , …am线性无关的充分必要条件是齐次线性方程组只有零解.
。、
向量维度是竖向的,即齐次方程的方程数。向量个数是横向的,齐次方程的未知数个数
未知数大于方程数,则说明该齐次方程组,必有非零解,该向量组必线性相关
如果向量组是方阵,可以用行列式不为0可推出齐次方程有解
反之线性无关,其行列式不为0,AX仅有零解。
5、非齐次方程有解,向量组线性相关(改写定理4)
6、部分向量组线性相关,整体必相关
向量个数的加减:
向量组部分线性相关,则整体也线性相关;整体线性无关,则任一部分都线性无关.(增加向量个数,提高相关性)
总结:部分相关,整体相关。整体无关,部分无关
7、无关向量增加维度,依旧无关
向量维度的增减:
向量组原本无关,增加向量维度(即增加方程个数),依旧无关;向量组原本线性相关,缩短向量组维度,向量组依旧相关
秩的大总结
矩阵的秩(不等式)
证明:
被表示的秩不大可以这么理解:被表示的向量组是低维的,高维向量组可以表示低维向量组
向量组的秩
关于秩和线性表示及初等变换的关系
极大无关组的求法
等价向量组
向量组和它的极大线性无关组是等价向量组
等价向量组和矩阵等价
向量组等价还要两组向量中的一组可以通过另一组向量的线性组合来表示
矩阵的秩与伴随矩阵的秩
证明:
齐次方程组(非齐次方程组)与向量组
所以从本质上说,方程组问题就是向量组问题,方程组和向量组是同一个问题的两种表现形式,其本质一样,所以解决方法也一样。
齐次方程组的特性
有解的条件
解的性质
解集1是齐次方程组的解,解集2是齐次方程组的解,解集1和解集2的线性组合也是方程组的解
基础解系和解的结构
通解的含义:无穷多解是一个解空间,而通解则是可以表达出这个解空间的线性组合
基础解系的相关概念:详情跳转
解齐次方程组的大致流程
化为阶梯型矩阵时,只能用初等行变换。
求基础解系的方式
注意:主元不一定在首位
齐次方程组有非零解的解法
1、先化出该其次线性方程组的系数矩阵
2、根据克拉默法则,当系数矩阵的行列式为0时,该线性方程组有非零解
依据定理4.2可得参数a的结果如下:
3、当求得的参数a代入回系数矩阵,求它们的通解(即解向量)
解非齐次方程组的大致流程
有解与无解的情况
解的性质
求非齐次的解的步骤
1、通过初等行变换化成阶梯型矩阵,也是先看是否有解(通过矩阵的秩和增广矩阵的秩是否相等)
2、若有解,将阶梯型矩阵主元化作1,化为最简矩阵后,再画出方程组。
3、如上所示,设自由变量为k,用自由变量来表示主变量,就是设自由变量为k
基础解系与秩的关系
还需要注意的是,这个n指的是未知量个数,而不是n阶矩阵
小结(方程组解)
方程组的解就是描述列向量组中各向量之间数量关系的系数。
抽象型线性方程组求解(四种基本问题)
方程组有解的条件和判别
非齐次的特解与通解的情况
非齐次特解的构造
方程组Ax=0的基础解系的讨论
线性方程组系数矩阵列向量和解的关系
“方程组的解就是描述列向量组中各向量之间数量关系的系数."
求公共解和同解
公共解
类似两个方程联立求共解,只不过线性代数的方程是“解空间”,所以其多个方程的公共解也是解空间的形式。
同解
用同解求秩相等
转置不改变矩阵的秩














































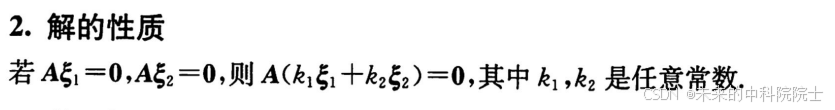








































 1031
1031

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








